Diagrama funcional en el sistema de control.
Usando diagramas de bloques al examinar sistemas más grandes, la atención se puede dirigir a un número menor de elementos o subsistemas cuyas propiedades ya se conocen. Al hacerlo, se crea una serie de bloques individuales que representan los diversos elementos o subsistemas, y estos bloques se interconectan para representar el sistema completo. Cada bloque representa la función de transferencia de un subsistema o elemento en particular, y la función y el desempeño de todo el sistema pueden analizarse estudiando el efecto de las interconexiones. Los bloques interconectados representan entonces las ecuaciones diferenciales del sistema de control. En algunos casos, los bloques son simplemente constantes que representan ganancias del sistema, como constantes de amplificación, escala o generador.
Por lo tanto, el diagrama de bloques sirve como una ayuda organizativa y visual que se puede reducir y simplificar a un sistema lineal. Al separar un sistema más grande en subsistemas o componentes más pequeños, los límites de la interfaz deben elegirse de modo que el efecto de carga de los sistemas adyacentes no cambie las características o la función de transferencia de un elemento del modelo en particular. Algunas características comunes en un diagrama de bloques se dan a continuación.
- También puedes leer: Ventajas y desventajas del sistema de control de retroalimentación
Bloques simples
Un sistema o elemento cuya función de transferencia es G(s) puede representarse mediante un diagrama de bloques, como se muestra en la figura.
Fig.1: Diagrama de bloques de la función de transferencia G(s)
Si la función de transferencia es K constante, se utiliza el diagrama de la siguiente figura.
Fig.2: Diagrama de bloques de la constante K
Estos bloques representaban las ecuaciones algebraicas:
$Y(s)=G(s)X(s)$
Y
$Y(s)=KX(s)$
A veces, el valor de la función de transferencia se muestra en el bloque, como se muestra en la siguiente figura, para el sistema de primer orden.
Fig.3: Sistema de primer orden
Los bloques en las siguientes figuras muestran integración y diferenciación escaladas.
Fig.4: Integración
Fig.5: Diferenciación
Bloques en cascada
La salida del bloque suele ser la entrada de otro bloque, como se muestra en la figura:
Fig.6: Sistemas individuales
El segundo bloque no debería afectar el rendimiento del primer bloque; de hecho, por lo tanto, el segundo bloque debe ofrecer una impedancia de entrada relativamente alta. Si la interacción de los bloques cambiará las funciones de transferencia individuales, debemos analizar para combinar los bloques en uno antes de usarlos en el diagrama.
Como se muestra en la siguiente figura, los elementos en cascada se pueden combinar en un bloque de acuerdo con el álgebra del diagrama de bloques como
Fig.7: Sistemas combinados
$frac{Z(s)}{X(s)}=left[ frac{Y(s)}{X(s)} right] izquierda[ frac{Z(s)}{Y(s)} right]={{G}_{1}}(s){{G}_{2}}(s)$
Para sistemas lineales, la conmutación de los bloques individuales, es decir
${{G}_{1}}(s){{G}_{2}}(s)={{G}_{2}}(s){{G}_{1}}(s) ps
Como extensión, cualquier número de bloques en cascada se puede combinar en un solo bloque multiplicando las funciones de transferencia.
Comparador y punto de suma
En el dominio s, el siguiente diagrama representa un sumador para expresar la función:
$e


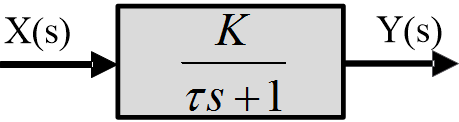
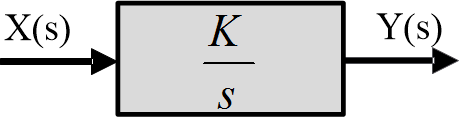
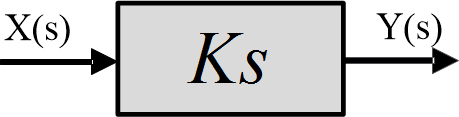

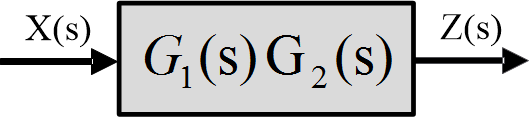
¡Más Contenido!