Ejemplo de diagrama de Bode | Diagrama posterior Ejemplo de MATLAB

Diagrama de Bode Un ejemplo de un sistema de primer orden usando Matlab

En este articulo, Diagrama de Bodas de la red de cambio de fase simple (sistema de primer orden) se obtiene usando Matlab. Para trazar el diagrama de Bode, necesitamos una función de transferencia de la que obtengamos las ecuaciones Tamaño y La licenciatura.

[G(s)=frac{1}{2s+1}]

La función en el dominio de la frecuencia se puede escribir:

[G(s)=frac{1}{2jomega +1}]

De la expresión anterior, podemos derivar la frecuencia de esquina o punto de ruptura;

[omega =frac{1}{2}]

Para el tamaño de la parcela:

Cuando ω<<1 (valor muy pequeño), entonces

$G(s)alrededor de $1

Así, para un valor muy pequeño de ω, la magnitud de la función de transferencia sería logarítmica;

[|G(jomega ){{|}_{dB}}=20text{ }log|G(jomega )|=20text{ }log(1)=0]

Por lo tanto, la respuesta de amplitud sería constante por debajo del punto de ruptura.

Cuando ω>>1 (valor muy grande), entonces

[G(s)approx frac{1}{2jomega }]

Por tanto, para un valor muy grande de ω, la magnitud de la función de transferencia sería logarítmica;

[|G(jomega ){{|}_{dB}}=20text{ }log|G(jomega )|=20text{ }logleft| frac{1}{|2jomega |} right|=20text{ }logleft( frac{1}{2omega } right)=20logleft| 1 right|-20logleft| 2omega  right|=-20log(2omega )]

Entonces, por encima del punto de ruptura, el gráfico de magnitud sería una línea recta con una pendiente de -20 dB/década.

Ahora el grado de la función de transferencia G(s) se puede calcular como;

[angle G(jomega )=0-{{tan }^{-1}}(omega T)={{tan }^{-1}}(omega T)]

Para el diagrama de fase:

Cuando ω es muy pequeño (ω≈0), entonces

[angle G(jomega )H(jomega )={{0}^{centerdot }}]

Cuando ω es muy grande (ω→∞), entonces

[angle G(jomega )H(jomega )=-{{90}^{centerdot }}]

Ejemplo de diagrama de código de Matlab

Aquí hemos implementado el diagrama de Bode para una comprensión completa de los lectores.

% Bode Plot for Phase-Lag Network Example

clc

% Transfer function

K = [1];

T = 2;

num = [K];

den = [T 1];

H = tf(num, den)

% Bode Plot

grid on

bode(H)

grid

%For Asymptotic Plot

% num=[1];

% den=[2 1];

% bode_asymptotic(num,den);

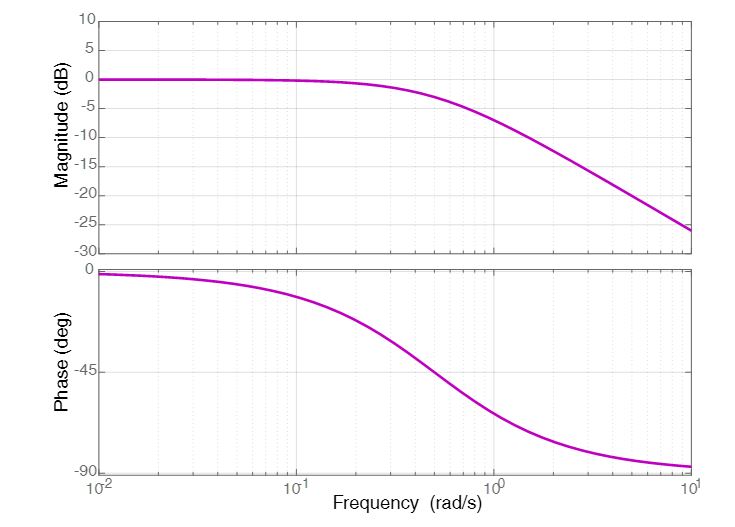
Diagrama de una caldera para un ejemplo de red de cambio de fase

• También puedes leer: Introducción detallada al Diagrama de Bode con Matlab