Perturbaciones tales como sobrecargas y cortocircuitos afectan el funcionamiento normal del sistema eléctrico de estado estable, a veces de manera significativa. Los cortocircuitos son las principales áreas de preocupación, no solo porque pueden causar un daño significativo al componente del sistema afectado, sino también porque pueden provocar inestabilidad en todo el sistema de energía. Por lo tanto, es necesario diseñar sistemas de protección para minimizar los riesgos asociados a la ocurrencia de perturbaciones.
El diseño de estos sistemas de protección se basa en el análisis de fallas. La coordinación correcta de los relés de protección y la especificación correcta de los valores nominales de los interruptores automáticos se basan en los resultados de los cálculos de fallas. El rendimiento del sistema eléctrico se simula en lo que se denomina un análisis de estabilidad transitoria bajo diversas perturbaciones, como cortocircuitos, cambios de carga grandes y repentinos y operaciones de conmutación.
La protección de la red eléctrica es una preocupación importante ya que los cortocircuitos presentan riesgos de daño al equipo y pérdida de sincronización de las máquinas síncronas. La tercera parte de este capítulo trata sobre los diferentes tipos de sistemas de protección y su aplicación para proteger los diferentes componentes del sistema eléctrico.
Los estudios de estabilidad transitoria investigan la capacidad del sistema de energía para permanecer sincronizado durante perturbaciones importantes, como fallas de equipos, grandes cambios de carga o fallas momentáneas. Los conceptos básicos de estabilidad se presentan en la sección final, junto con una breve descripción de modelos para generadores, sistemas de excitación y sistemas de turbina-gobernador.
Análisis de fallas
El modo típico de operación de un sistema de potencia es la corriente alterna trifásica balanceada. Sin embargo, existen eventos indeseables pero inevitables que pueden alterar temporalmente las condiciones normales, por ejemplo, cuando el aislamiento del sistema falla en algún punto o cuando el material conductor entra en contacto con un conductor desnudo. Entonces se dice que ha ocurrido una falla. Una falla puede ser causada por rayos, caída de árboles sobre líneas eléctricas, colisión de vehículos con postes o pilones, vandalismo, etc.
Las fallas se pueden clasificar en cuatro tipos. Los diferentes tipos de fallas se enumeran aquí en orden de frecuencia de ocurrencia.
- Falla de línea única (SLG).
- Falla de línea a línea (LL).
- Alivio de línea a tierra doble (2LG)
- Alivio trifásico balanceado
Los cálculos de fallas brindan información sobre corrientes y voltajes en un sistema eléctrico durante condiciones de falla. Las corrientes de cortocircuito se calculan para cada posición de relé y disyuntor y para diversas condiciones de contingencia del sistema, como líneas o generadores fuera de servicio, para determinar las corrientes de falla mínimas y máximas. Esta información es útil para el ingeniero en la selección de interruptores automáticos para interrupción de fallas, selección de relés para detección de fallas y determinación de parámetros de relés, conocidos como coordinación de relés. La selección y colocación adecuada de los dispositivos de protección garantiza que el servicio eléctrico no se interrumpa y limita los posibles daños a los equipos defectuosos.
Análisis de fallas trifásicas
Se puede lograr una precisión adecuada en los estudios de fallas con ciertas simplificaciones en el modelo del sistema de potencia. Estos supuestos incluyen:
- Se desprecian los elementos de derivación del modelo del transformador; es decir, se omiten las corrientes de magnetización y las pérdidas en el núcleo.
- La capacitancia en derivación se desprecia en el modelo de línea de transmisión.
- Los transformadores están configurados en posiciones de derivación nominales.
- Todas las fuentes de voltaje internas se configuran igual a 1.0∠0°. Esto es equivalente a despreciar las corrientes de carga previas a la falla.
Los cálculos de fallas trifásicas se pueden realizar paso a paso porque el sistema eléctrico permanece efectivamente equilibrado o simétrico durante una falla trifásica. Por lo tanto, los diversos componentes del sistema de potencia están representados por circuitos equivalentes monofásicos en los que se supone que todas las conexiones trifásicas se convierten en conexiones en estrella equivalentes. Los cálculos se realizan utilizando impedancias por fase, corrientes de fase y tensiones de línea-neutro.
Análisis de fallas, como cualquier otro cálculo del sistema eléctrico, es más fácil de hacer usando la representación por unidad. Los componentes del sistema de potencia se describen en términos de impedancias unitarias o admitancias unitarias.
el es basado en el poder se selecciona y se utiliza para todas las partes del sistema de potencia. el es bases de voltaje que son diferentes para diferentes partes del sistema, y se eligen de modo que la relación de vueltas por unidad de transformador sea igual a la unidad. el es base actual y calcule la base de impedancia utilizando la base de potencia y la base de voltaje especificadas.
Falla de línea única a tierra
Una falla de línea a tierra (SLG) es la falla más común falla asimétrica. Podría ser el resultado de un accidente automovilístico que provoque que uno de los conductores de fase se caiga y haga contacto con la tierra, o podría ser el resultado de la caída de ramas de árboles, o podría deberse a descargas disruptivas a través de aisladores de polvo durante las lluvias. En la figura 1 se muestra una falla de una sola línea a tierra. 1.
Suponiendo que las corrientes previas a la falla son insignificantes, la falla SLG se describe mediante las siguientes relaciones de voltaje y corriente.
$begin{matriz} {{V}_{a}}=0 & {} & left( 1 right) end{matriz}$
$begin{matriz} {{I}_{b}}={{I}_{c}}=0 & {} & left( 2 right) end{matriz}$
Los componentes de secuencia de la corriente de cortocircuito se encuentran con la siguiente ecuación. Asi que,
[begin{matrix} left[ begin{matrix} {{I}_{a0}} {{I}_{a1}} {{I}_{a2}} end{matrix} right]=frac{1}{3} izquierda[ begin{matrix} 1 & 1 & 1 1 & a & {{a}^{2}} 1 & {{a}^{2}} & a end{matrix} right] izquierda[ begin{matrix} {{I}_{a}} 0 0 end{matrix} right] & {} & left( 3 right) end{matriz}]
Por lo tanto, todos los componentes de la secuencia de flujo se ven idénticos entre sí; Esto es,
$begin{matriz} {{I}_{a0}}={{I}_{a1}}={{I}_{a2}}=frac{1}{3}{{I}_{ a}} & {} & left( 4 right) end{matriz}$
El voltaje de la fase principal aa se puede expresar en términos de sus componentes de secuencia como
$begin{matriz} {{V}_{a}}={{V}_{a0}}+{{V}_{a1}}+{{V}_{a2}}=0 & {} & left( 5 right) end{matriz}$
La aplicación de KVL a la figura 2 da la siguiente ecuación:
$begin{matriz} {{E}_{a1}}-{{I}_{a1}}left( {{Z}_{1}}+{{Z}_{2}}+{{ Z}_{o}} right)=0 & {} & left( 6 right) end{matriz}$
La expresión para yoa1 obtenido de la Ec. 6, y usando la ec. 4 proporciona las oraciones para Ia2 y yo mismoa0 como sigue:
[begin{matrix} {{I}_{a1}}=frac{{{E}_{a1}}}{{{Z}_{1}}+{{Z}_{2}}+{{Z}_{0}}}={{I}_{a2}}={{I}_{a0}} & {} & left( 7 right) end{matrix}]
La corriente de cortocircuito Ia se obtiene como la suma de sus componentes de secuencia; Asi que,
[begin{matrix} {{I}_{a}}={{I}_{a0}}+{{I}_{a1}}+{{I}_{a2}}=3frac{{{E}_{a1}}}{{{Z}_{1}}+{{Z}_{2}}+{{Z}_{0}}} & {} & left( 8 right) end{matrix}]
Las ecuaciones 4 y 5 muestran que las redes de secuencia deben interconectarse en serie para una sola falla de línea a tierra. Esto se muestra en la figura. 2.
Figura 1: Alivio de una línea a tierra.
Figura 2: Redes de secuencia de interconexión desde una sola línea hasta falla a tierra
Fallo línea a línea
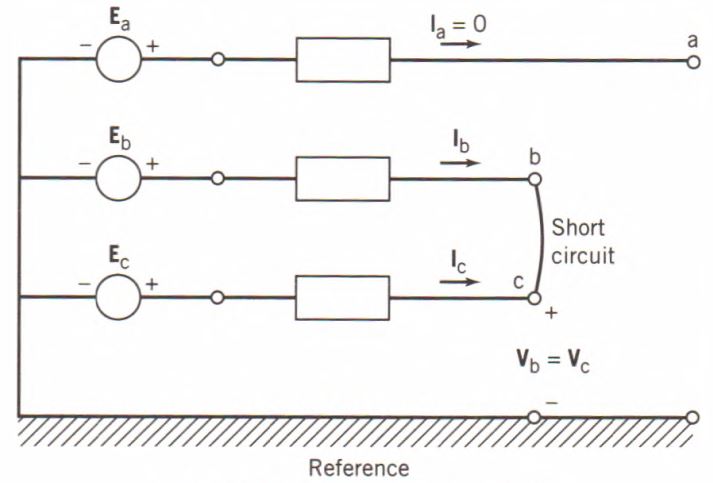
Una falla de línea a línea (LL) es un cortocircuito entre dos conductores de fase que se consideran las fases b y c. Por lo tanto, hay simetría con respecto a la fase principal a. Una falla de línea a línea se muestra en la Fig. 3.
Suponiendo que las corrientes previas a la falla son insignificantes, la relación entre el voltaje y la corriente que describe la falla línea a línea está dada por
$begin{matriz} {{V}_{b}}={{V}_{c}} & {} & left( 9 right) end{matriz}$
$begin{matriz} {{I}_{b}}=-{{I}_{c}}; & {{I}_{a}}=0 & left( 10 right) end{matriz}$
Figura 3: Una falla de línea a línea.
Se encuentra los componentes de secuencia de la corriente de cortocircuito con la siguiente ecuación. Asi que,
[begin{matrix} left[ begin{matrix} {{I}_{a0}} {{I}_{a1}} {{I}_{a2}} end{matrix} right]=frac{1}{3} izquierda[ begin{matrix} 1 & 1 & 1 1 & a & {{a}^{2}} 1 & {{a}^{2}} & a end{matrix} right] izquierda[ begin{matrix} {{I}_{a}} {{I}_{b}} {{I}_{c}} end{matrix} right]=frac{1}{3} izquierda[ begin{matrix} 0 left( a-{{a}^{2}} right){{I}_{b}} left( {{a}^{2}}-a right){{I}_{c}} end{matrix} right] & {} & left( 11 right) end{matriz}]
Por tanto, vemos que la componente directa de la corriente es igual al negativo de su componente directa; Esto es,
$begin{matriz} {{I}_{a2}}=-{{I}_{a1}} & {} & left( 12 right) end{matriz}$
Los voltajes de las fases en cortocircuito, b y c, se pueden expresar en términos de componentes de secuencia de la siguiente manera:
$begin{matriz} {{V}_{b}}={{V}_{a0}}+{{a}^{2}}{{V}_{a1}}+a{{V} _ {a2}}=0 & {} & left( 13 right) end{matriz}$
$begin{matriz} {{V}_{c}}={{V}_{a0}}+a{{V}_{a1}}+{{a}^{2}}{{V} _ {a2}}=0 & {} & left( 14 right) end{matriz}$
Restar la ec. da 14 de 13
$begin{matriz} {{V}_{b}}-{{V}_{c}}=({{a}^{2}}-a){{V}_{a1}}+( a-{{a}^{2}}){{V}_{a2}} & {} & left( 15 right) end{matriz}$
porque Vb y Vcontra igual, Ec. 15 se reduce a cero y da
$begin{matriz} {{V}_{a1}}={{V}_{a2}} & {} & left( 16 right) end{matriz}$
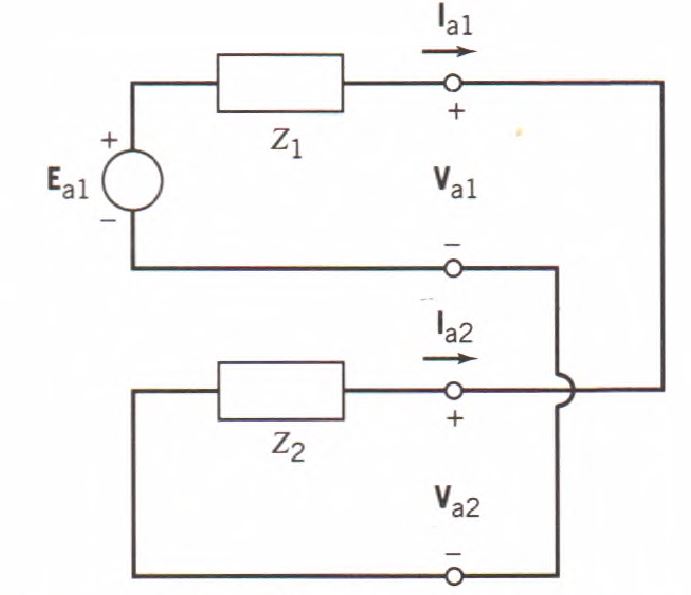
Las ecuaciones 12 y 16 muestran que las redes de secuencia positiva y negativa deben estar interconectadas en paralelo para una falla de línea a línea. Esto se muestra en la figura. 4.
Figura 4: Redes secuenciales de interconexión por falta entre líneas.
Falla de doble línea a tierra
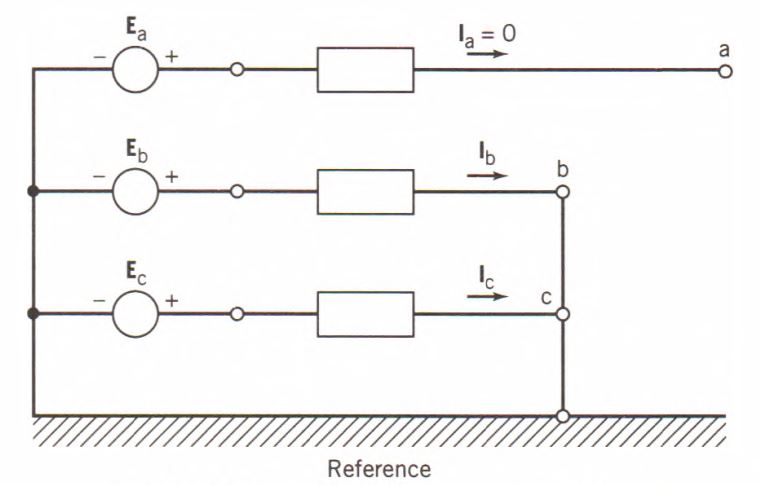
Una falla de doble línea a tierra (2LG) es un cortocircuito entre dos conductores de fase vendado c y tierra. Para la falla línea a línea, existe simetría con respecto a la fase principal a. Una falla doble de línea a tierra se muestra en la Fig. 5.
Para una falla 2LG con corrientes de falla directa insignificantes, la relación entre el voltaje y la corriente viene dada por:
$begin{matriz} {{V}_{b}}={{V}_{c}}=0 & {} & left( 17 right) end{matriz}$
$begin{matriz} {{I}_{a}}=0 & {} & left( 18 right) end{matriz}$
Los componentes de secuencia del voltaje en la ubicación de la falla se encuentran usando la siguiente ecuación. Asi que,
[begin{matrix} left[ begin{matrix} {{V}_{a0}} {{V}_{a1}} {{V}_{a2}} end{matrix} right]=frac{1}{3} izquierda[ begin{matrix} 1 & 1 & 1 1 & a & {{a}^{2}} 1 & {{a}^{2}} & a end{matrix} right] izquierda[ begin{matrix} {{V}_{a}} 0 0 end{matrix} right]=frac{1}{3} izquierda[ begin{matrix} {{V}_{a}} {{V}_{a}} {{V}_{a}} end{matrix} right] & {} & left( 19 right) end{matriz}]
Por lo tanto, se ve que las componentes de secuencia del voltaje en la falla son todas iguales; Esto es,
$begin{matriz} {{V}_{a1}}={{V}_{a2}}={{V}_{a0}} & {} & left( 20 right) final {matriz}$
FIGURA 5 Alivio de doble línea a tierra.
Despreciando las corrientes de carga previas a la falla, la corriente en la fase aa se puede expresar como
$begin{matriz} {{I}_{a}}={{I}_{a0}}={{I}_{a1}}={{I}_{a2}}=0 & {} & left( 21 right) end{matriz}$
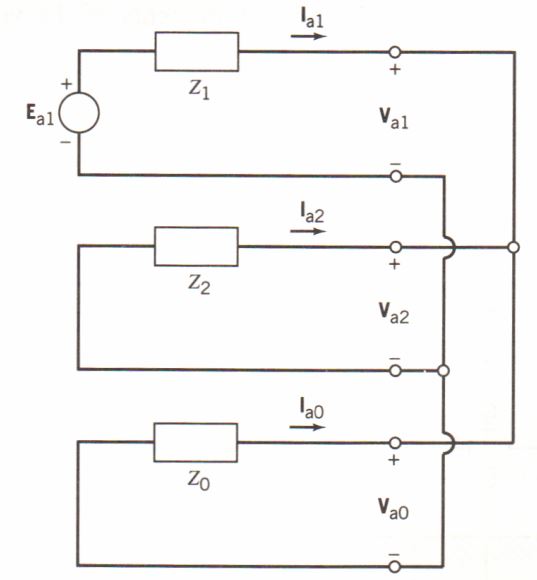
Las ecuaciones 20 y 21 muestran que las tres redes de secuencia deben estar interconectadas en paralelo para una falla doble línea a tierra. Esto se muestra en la figura. 6.
Figura 6: Red de secuencia de interconexión para una falla doble línea a tierra
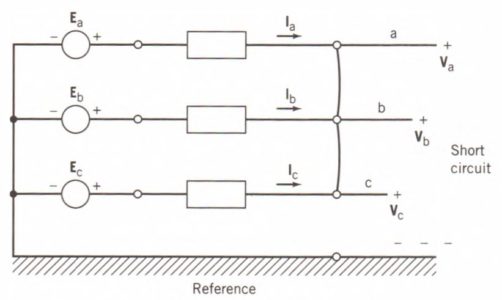
Falla trifásica
Una falla trifásica, aunque es una falla simétrica, también puede analizarse por el método de componentes simétricos. Considere la falla trifásica que se muestra en la Fig. 7. Suponiendo que las corrientes previas a la falla son insignificantes, la relación de voltaje y corriente que describe esta falla es
[begin{matrix} {{V}_{a}}={{V}_{b}}={{V}_{c}} & {} & left( 22 right) end{matrix}]
$begin{matriz} {{I}_{a}}={{I}_{b}}={{I}_{c}}=3{{I}_{a0}}=0 & { } & left( 23 right) end{matriz}$
La ecuación 23 confirma que no hay corriente cero para una falla trifásica; es decir que soya0 que es exactamente igual a cero. Los componentes directo e inverso del voltaje en la ubicación de la falla son:
$begin{matriz} {{V}_{a1}}=frac{1}{3}left( {{V}_{a}}+a{{V}_{b}}+{{ a}^{2}}{{V}_{c}} right)=frac{1}{3}left( 1+a+{{a}^{2}} right){{V} _ {a}}=0 & {} & left( 24 right) end{matriz}$
[begin{matrix} {{V}_{a2}}=frac{1}{3}left( {{V}_{a}}+{{a}^{2}}{{V}_{b}}+a{{V}_{c}} right)=frac{1}{3}left( 1+{{a}^{2}}+a right){{V}_{a}}=0 & {} & left( 25 right) end{matrix}]
Figura 7: Hay una falla trifásica
Dado que los componentes de voltaje directo e inverso en la ubicación de la falla son cero:
$begin{matriz} {{V}_{a1}}=-{{I}_{a1}}{{Z}_{1}}+{{E}_{a1}}&{}& izquierda( 26 derecha) final{matriz}$
$begin{matriz} {{V}_{a2}}=-{{I}_{a2}}{{Z}_{2}} & {} & left( 27 right) end {matriz}$
Los componentes de secuencia de la corriente se obtienen a partir de las ecuaciones. 26 y 27 de la siguiente manera:
$begin{matriz} begin{alineación} & {{I}_{a1}}=frac{{{E}_{a1}}}{{{Z}_{1}}} & { {I}_{a2}}=0 final{alinear} & {} & left( 28 right) final{matriz}$
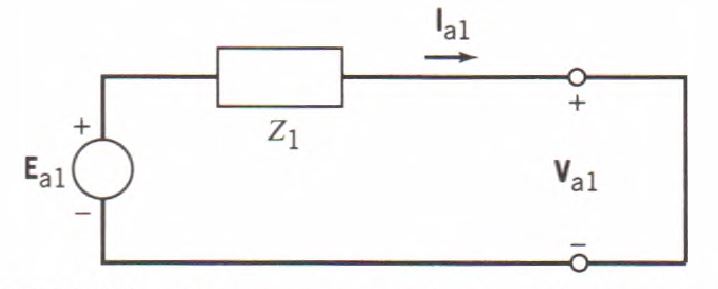
Se encontró que no fluye corriente inversa ni de secuencia cero durante una falla trifásica. Por lo tanto, el análisis de fallas trifásicas solo se aplica a la red directa, que se muestra en la Fig. 8.
Figura 8: Red de secuencias para una falta trifásica.


¡Más Contenido!