Sistema simulador de solución de alta precisión con función de inyección de fallas
Introducción
Dado que las soluciones tienen una excelente fiabilidad y un rendimiento de alta precisión en entornos duros y severos durante mucho tiempo, se utilizan ampliamente en vehículos eléctricos, vehículos eléctricos híbridos, EPS, inversores, servomotores, vías férreas, vías férreas de alta velocidad, aeroespacial y otros. aplicaciones donde se requiere información de posición y velocidad.
Muchos convertidores de resolver a digital (RDC), como el AD2S1210 y el AD2S1205, se utilizaron en sistemas anteriores para decodificar la señal del resolver para obtener datos digitales de posición y velocidad. Los problemas de interferencia y falla generalmente ocurren en los sistemas de los clientes, y la mayoría de las veces quieren evaluar la precisión del ángulo y el rendimiento de la velocidad en las condiciones de interferencia, encontrar y validar la causa raíz, luego reparar el sistema y optimizarlo. Un simulador de rectificador de alta precisión (que simula un rectificador conectado al motor real a velocidad o posición constante) con inyección de fallas puede resolver problemas de interferencias y fallas sin configurar un sistema de control de motor complejo.
Este artículo analizará la contribución de los errores en los sistemas de simulación de árbitros y brindará algunos ejemplos de cálculo de errores para ayudar a comprender por qué la alta precisión es tan importante en los simuladores de árbitros. Luego mostrará la condición de falla en condiciones de interferencia en las solicitudes de campo. A continuación, se describe cómo construir un simulador de soluciones de alta precisión con funciones de inyección y simulación de fallas utilizando los últimos productos de alta precisión. Finalmente, mostrará algunas de las capacidades del simulador de casting.
Contribuciones de error en sistemas de simulación de solver
Primero, esta sección presentará la estructura ideal de la solución. A continuación, se presentarán cinco características no ideales y métodos de análisis de errores para ayudarlo a comprender por qué se requiere una alta precisión en los sistemas de simulación de solucionadores.
El simulador de solucionador simulará un solucionador, como se muestra en la Figura 1, conectado a un motor real a velocidad constante o posición constante. En el caso de rectificadores convencionales de reluctancia o variables, se incluye un rotor y un estator. Se puede pensar en un resolver como un transformador especial. En el lado primario, como se expresa en la ecuación 1, EXC es la señal de entrada de excitación sinusoidal. En el lado secundario, como se muestra en la ecuación 2 y la ecuación 3, SIN y COS son la señal de onda sinusoidal modulada en las dos salidas.



lugar:
θ es el ángulo del eje, ω es la frecuencia de la señal de excitación, A0 es la amplitud de la señal de excitación, y j La relación de transformación es resolver.
Las señales SIN/COS moduladas se muestran en la Figura 2. Para un ángulo constante θ en diferentes cuadrantes, la señal SIN/COS tendrá situaciones en fase y antifase. Para velocidad constante, la frecuencia de la envolvente SIN/COS es constante y representa la información de velocidad.
Para cada uno de los productos RDC ADI, la señal de demodulación se expresa en la Ecuación 4. Se eliminará un bucle de seguimiento Tipo II cuando φ (ángulo de salida digital) igual a θ (posición del rotor), ángulo del resolver. En un sistema de resolución real con compensación de amplitud, cambio de fase, cuadratura imperfecta, armónicos de excitación y armónicos inducidos, cualquiera de estas cinco condiciones no ideales puede ocurrir y contribuir al error.
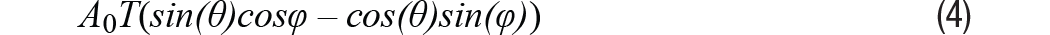
Desajuste de amplitud
La compensación de amplitud es la diferencia entre las amplitudes de pico a pico de las señales SIN y COS cuando están en su amplitud máxima, con 0° y 180° para COS, y 90° y 270° para SIN. Un desajuste puede ser introducido por diferencias en los devanados del resolver o por un control de ganancia desequilibrado en la entrada SIN/COS. Para determinar el error de posición causado por el desajuste de amplitud, la ecuación 3 se puede reescribir como la ecuación 5.
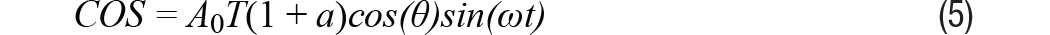
Dónde a La cantidad de compensación entre las señales SIN y COS es la misma, la señal de envolvente que queda después de la demodulación se puede mostrar fácilmente, como en la ecuación 6. Cuando la señal de envolvente se lleva a cero en un bucle de seguimiento como II, configurando la ecuación 6 para cero, el error de posición se puede encontrar ε = θ – φ. Entonces podemos obtener información de error como se muestra en la Ecuación 7.
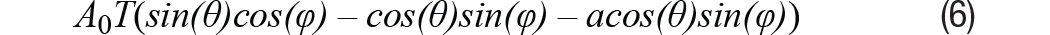

Para la situación realista cuando a es pequeño, el error de posición también es pequeño, lo que sugiere que sen(ε) ≈ ε y θ + φ ≈ 2θ. Así, la ecuación 7 se convierte en la ecuación 8 con el término de error expresado en radianes.

Como se muestra en la ecuación 8, el término de error oscila al doble de la velocidad de rotación y el error máximo a/2 se alcanza en múltiplos enteros impares de 45°. Suponga que el desplazamiento de amplitud es 0.3%, sustituya las variables en la Ecuación 8 y, usando un entero impar múltiplo de 45°, el error máximo se mostrará en la Ecuación 9, cuando metro es un entero impar.
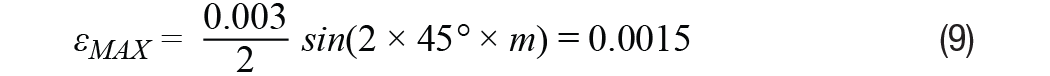
El error, calculado en radianes, se puede convertir a LSB mediante la ecuación 10, donde el modo RDC es de 12 bits, o aproximadamente 1 LSB.
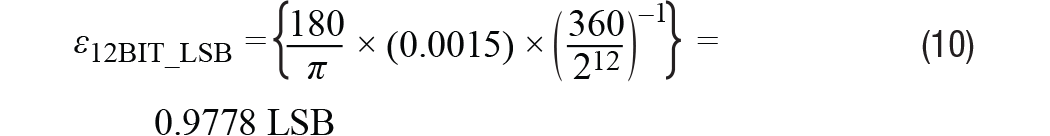
cambio de grado
El cambio de fase se refiere tanto al cambio de fase diferencial como al cambio de fase común. El cambio de fase diferencial es el cambio de fase entre las señales SIN y COS del resolver. El cambio de fase común es el cambio de fase entre la señal de referencia de excitación y las señales SIN y COS. Para determinar el error de posición creado por el cambio de fase diferencial, la ecuación 3 se puede reescribir como la ecuación 11.
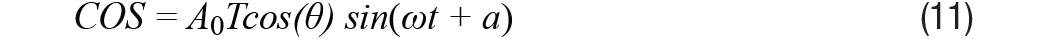
Dónde a El cambio de fase diferencial es el mismo, la señal de envolvente que queda después de la demodulación se puede expresar mediante la ecuación 12 donde el término de cuadratura cos(peso)(sen(a)sen(θ)cos(φ)) inatención. Para la situación realista cuando a poco, como (a) ≈ 1 - a2/2. Al conducir esta señal a cero en un bucle de seguimiento de tipo II, con la ecuación 10 establecida en cero, se puede encontrar el error de posición ε = θ – φ como resultado. Entonces podemos obtener información de error como se muestra en la Ecuación 13.
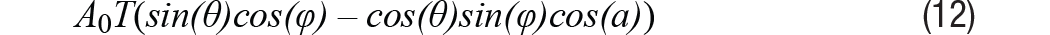

Para θ ≈ φ, sen(θ)cos(φ)hay un máximo de 0,5 a θ ≈ 45°. Así, la ecuación 13 se convierte en la ecuación 14 con el término de error expresado en radianes.

Suponiendo que el cambio de fase diferencial sea de 4,44°, el error, que se puede convertir a LSB usando la Ecuación 15 cuando el modo RDC es de 12 bits, es de aproximadamente 1 LSB.
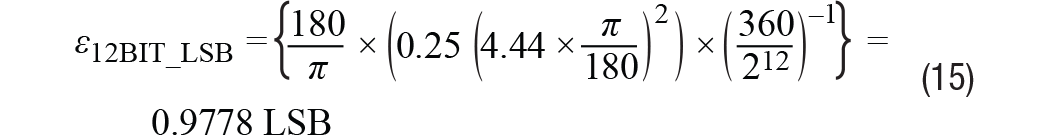
Cuando el cambio de fase es común βLa Ecuación 2 y la Ecuación 3 se pueden reescribir como Ecuación 16 y Ecuación 17, respectivamente.

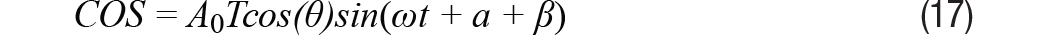
De manera similar, el término de error se puede expresar en la Ecuación 18.

En condiciones de funcionamiento estático, un cambio de fase común no afectará la precisión del convertidor, pero los resolvers de alta velocidad generarán voltajes de velocidad debido a los componentes reactivos de la impedancia del rotor y las señales de interés. Voltaje de velocidad, que solo ocurre a velocidad y no en ángulos estáticos, que están en cuadratura con la señal de interés. Cuando el cambio de fase es común βel error de seguimiento se puede aproximar mediante la ecuación 19, donde ωMETRO es la velocidad del motor y ωmi La velocidad es la excitación.

Como se muestra en la Ecuación 19, el error es proporcional a la velocidad y el cambio de fase del solucionador. Por tanto, en general, es ventajoso utilizar una frecuencia de excitación de alta resolución.
Un cuarteto imperfecto
Una cuadratura imperfecta indica que las dos señales de resolución a las que se refiere SIN/COS en este caso no están en un cuadrante exacto de 90°. Esto ocurre cuando los dos pasos de fundición no se mecanizan o ensamblan en perfecta alineación espacial. Cuando β es igual al tamaño del cuadrante imperfecto, la ecuación 2 y la ecuación 3 se pueden reescribir como la ecuación 20 y la ecuación 21.


Como antes, la señal de envolvente que queda después de la demodulación se puede representar fácilmente mediante la ecuación 22. Poniendo la ecuación 22 a cero, suponga β poco, porque(β) ≈ 1 y sen(β) ≈ β, se puede encontrar la ubicación del error ε = θ – φ como resultado. Entonces podemos obtener información de error como se muestra en la Ecuación 23.
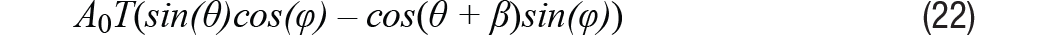
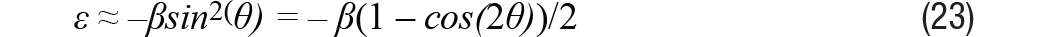
Como se muestra en la ecuación 23, el término de error oscila al doble de la velocidad de rotación, con un error máximo de β/2 se alcanza en múltiplos enteros impares de 45°. En cuanto al error debido al desplazamiento de amplitud, en este caso el error medio es distinto de cero y el error máximo es igual al error cuadrático. Del ejemplo de cambio de amplitud, cuando β = 0,0003 radianes = 0,172°, esto podría causar un error de aproximadamente 1 LBS en el modo de 12 bits.
excitación armónica
En todos los análisis anteriores, se supuso que la señal de excitación era una sinusoide ideal sin armónicos adicionales. En un sistema real, la señal de excitación contiene armónicos. Por lo tanto, la ecuación 2 y la ecuación 3 se pueden reescribir como la ecuación 24 y la ecuación 25.
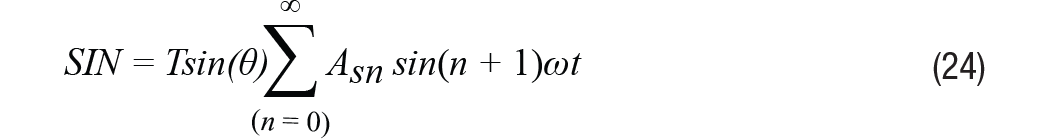
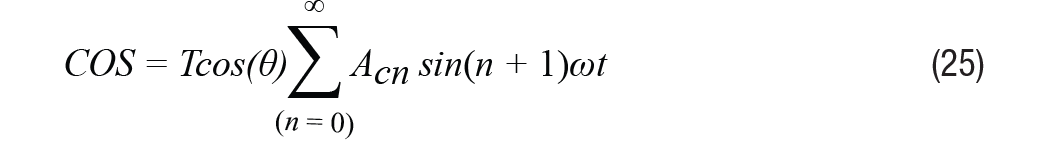
La señal de envolvente que queda después de la demodulación se puede representar fácilmente, como en la ecuación 26. Lleve esta señal a cero en el bucle de seguimiento de tipo II.
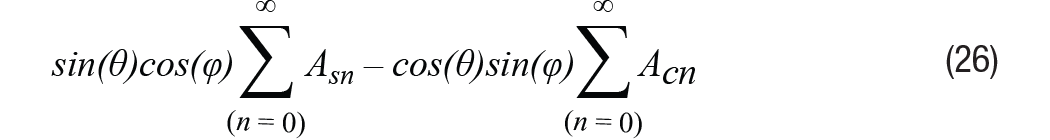
Establezca la ecuación 26 en cero y se puede obtener el error de posición ε = θ – φ como resultado. Entonces podemos obtener información de error como se muestra en la Ecuación 27.
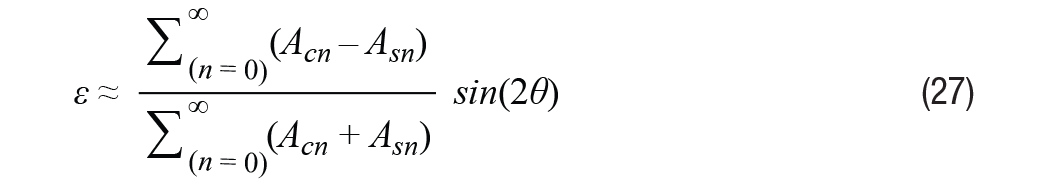
Si la excitación de la solución tiene un armónico igual, el numerador en la ecuación 27 es cero y no se incurre en error de posición. Esto significa que el armónico de excitación común tiene un efecto insignificante en la CDR, incluso a valores muy altos. Sin embargo, si el contenido armónico es diferente en SIN o COS, el error de posición tiene la misma forma funcional que el cambio de amplitud que se muestra en la Ecuación 8. Esto afectará en gran medida la precisión de la posición.
armónicos inductivos
En el mundo real, es imposible construir un solucionador con perfiles de inductancia que sean funciones de posición de seno y coseno perfectas. Por lo general, los inductores contendrán armónicos y las soluciones de realidad virtual contendrán componentes de CC. Por lo tanto, la ecuación 2 y la ecuación 3 se pueden reescribir como la ecuación 28 y la ecuación 29, respectivamente, cuando k0 representa el componente DC.
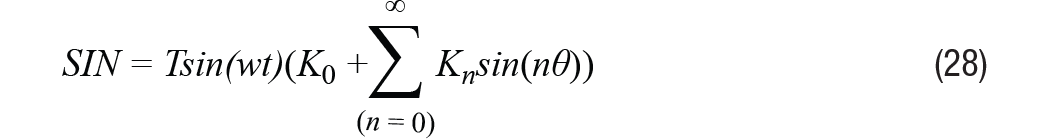

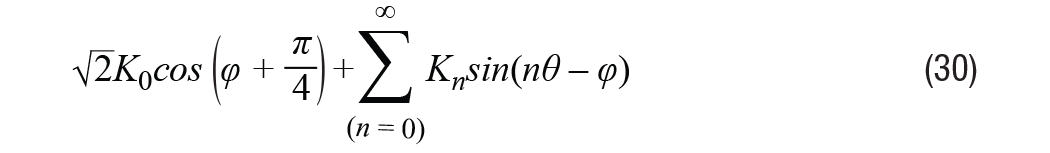
Se puede mostrar la señal de envolvente restante después de la demodulación, como en la ecuación 30.
Al llevar esta señal a cero en un bucle de seguimiento de tipo II, cuando las amplitudes armónicas son bajas, kno << 1 pour n > 1, información de error ε = θ – φ Se puede derivar de la ecuación 31.
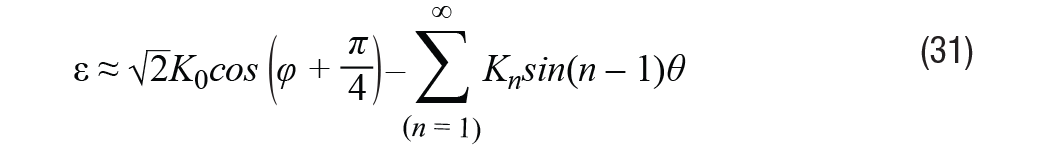
Según la expresión, el error es más sensible al término continuo que al efecto armónico, es proporcional a la amplitud armónica inducida. Mientras tanto, el nmi el armónico de inductancia determina la amplitud del (n - 1)mi error de posición armónica.
Resumen de la contribución de errores en un sistema simulador de soluciones
Aparte de la fuente de error mencionada, la interferencia a lo largo de las líneas SIN y COS, el error de compensación del amplificador, el error de polarización, etc., también pueden contribuir al error del sistema. El origen del error y el resumen de la contribución en el sistema del simulador del solucionador, incluido el ejemplo del peor caso de 1 LSB del método de 12 bits, se muestra en la Tabla 1. Se puede calcular otro método del solucionador RDC consultando la tabla.
Tipos de fallas en el sistema RDC
En los sistemas RDC reales, puede haber muchos escenarios de falla. Las siguientes secciones mostrarán diferentes tipos de fallas y algunos síntomas de fallas de las pruebas de campo, y cómo se puede simular el tipo de falla utilizando la solución del simulador de solucionador descrita en la tercera sección. Excepto por el tipo de falla mencionado, puede haber una interrupción aleatoria que conduzca a otra falla, o pueden ocurrir varias fallas al mismo tiempo.
Error de enlace incorrecto
Una mala conexión significa que la excitación del resolver y los pares SIN/COS están conectados a los pines de entrada y salida SIN/COS de excitación del RDC a través de conexiones incorrectas. Cuando se produce una desalineación, el RDC también puede decodificar información angular y de velocidad, pero los datos de salida angular mostrarán un salto, como un error de compensación en la salida del DAC. El caso de conexión y los detalles del resultado se muestran en la Figura 3. Donde la primera columna muestra los pines EXC/SIN/COS y el ángulo de salida, las otras columnas muestran los casos de conexión.
Alivio de cambio de paso
De la sección de contribución de error, sabemos que el cambio de fase consiste en un cambio de fase diferencial y un cambio de fase común. Considerando que la fase diferencial puede ser considerada como la diferencia de desfase común, en esta sección, la falla de desfase significa la falla causada por el desfase común.
La contribución común al error de cambio de fase se muestra en la Figura 4. La fase 1 corresponde al retraso del filtro de excitación. El paso 2 es el cambio de paso del solucionador. El paso 3 es un retardo de línea El paso 4 es el retardo del filtro SIN/COS. En un sistema de campo RDC, cuando ocurre un error de fase, significa que el valor total de las fases 1, 2, 3 y 4 es mayor a 44°. El error de cambio de fase del resolver es típicamente de 10°. En casos graves, el valor total de grados puede llegar a 30°. Para considerar MP se debe dejar un margen de grado suficiente.
Cuando el cambio de fase para SIN/COS es diferente, puede causar una falla de cambio de fase. Si esto sucede, la precisión angular y la velocidad se verán afectadas.
Error de desconexión
La falla de desconexión ocurre cuando una línea de resolución se desconecta de la interfaz de la plataforma RDC. Con la actualización de seguridad del producto, los clientes aún mencionan la detección de desconexión de línea. Esta falla se puede simular para llevar el SIN/COS a voltaje cero. Cuando se produce la desconexión, se puede activar un error LOS/DOS/LOT en AD2S1210.
Desajuste de amplitud/error de sobreresolución
El desequilibrio de amplitud ocurre cuando el control de ganancia del circuito o la relación de resolución de SIN/COS es diferente, lo que también significa que el valor de amplitud de la envolvente SIN/COS es diferente. Cuando la amplitud está cerca de AVDD, esto activará una falla de sobreimpulso de amplitud. En el caso del AD2S1210, esto se denomina falla de recorte. En la Figura 5 se muestra un buen ejemplo de una señal SIN/COS.
falla transitoria IGBT
La perturbación de IGBT significa la señal de interferencia junto con el efecto de encender/apagar el IGBT. Cuando la señal se combina con la línea SIN/COS, el rendimiento de la posición y la velocidad puede verse afectado, el valor angular saltará y la dirección de la velocidad puede cambiar. En la Figura 6 se muestra un ejemplo del terreno, donde el canal 1 es la señal SIN, el canal 2 es la señal COS y el cable representa una interferencia acoplada a la activación/desactivación de IGBT.
Falla de exceso de velocidad
La falla de sobrevelocidad ocurre cuando la velocidad eléctrica es mayor que la que resuelve el sistema de decodificación. Por ejemplo, en el modo de 12 bits, la velocidad máxima que AD2S1210 puede admitir es 1250 SPS, y cuando la velocidad eléctrica del resolver es 1300 SPS, se activará la falla de sobrevelocidad.
Arquitectura y descripción del sistema simulador de árbitro
Desde la primera parte, sabemos que el error de amplitud y fase determina directamente el rendimiento de decodificación del rendimiento angular y de velocidad. Afortunadamente, ADI tiene una amplia cartera de productos de precisión entre los que puede elegir y construir su sistema de simulador de resolución. La siguiente descripción mostrará cómo construir un simulador de solución de alta precisión y discutirá las partes a seleccionar.
El diagrama de bloques del simulador que se muestra en la Figura 7 tiene siete módulos en los que centrarse:
- La plataforma de control de procesos para el análisis y control de datos.
- El módulo de generación de reloj de sincronización genera un reloj de sincronización para el subsistema.
- El módulo de generación de señales de falla genera varias señales de falla.
- El módulo de generación SIN/COS genera señales SIN/COS moduladas como salidas del resolver.
- El módulo de adquisición de señales funciona como un módulo de adquisición de señales de excitación y realimentación.
- El módulo de salida SIN/COS gestiona la salida SIN/COS, incluidos el búfer, la ganancia y el filtro.
- El módulo de entrada de señal de excitación viene con un circuito integrado de tampón y filtro.
- El módulo de fuente de alimentación proporciona energía a los componentes ADC, DAC, conmutador, amplificador, etc.
El sistema de simulador de solver funciona haciendo que el módulo de captura de señal muestree la señal de excitación del módulo de entrada, donde el procesador analizará la frecuencia y la amplitud. El procesador calculará el código de datos de salida del DAC SIN/COS utilizando el algoritmo CORDIC y, a través del módulo SIN/COS, generará la misma señal sinusoidal de frecuencia que la entrada de excitación. Luego, el sistema recuperará simultáneamente las señales de excitación y SIN/COS, calculará y ajustará la fase/amplitud SIN/COS, compensará el error de fase entre la excitación y SIN/COS igual a cero y realizará la calibración SIN. /COS. Amplitud COS al mismo nivel. Finalmente, el sistema generará la señal SIN/COS modificada y la señal de falla para simular el rendimiento angular, la velocidad y la situación de falla.
La cadena de señal específica en la Figura 8 muestra un ADC SAR AD7380 dual-sim de 16 bits que se usa para capturar la señal de excitación y retroalimentación cuando OSR está habilitado y puede lograr una SNR de 98 dB. Es adecuado para la adquisición simultánea de datos de alta precisión para la calibración de fase y amplitud. Se utiliza un ADA4940-2 de potencia ultrabaja y baja distorsión como controlador ADC. Aunque el DAC AD5791 de alta precisión y bajo ruido de 20 bits se usa para generar el SIN/COS y la señal de falla para una resolución más baja y un costo más bajo, se recomienda reemplazar el AD5791 con el AD5541A o AD5781. Un amplificador diferencial de ganancia de precisión seleccionable, el AD8475, se utiliza como búfer de entrada/salida. Los amplificadores operacionales de precisión de riel a riel con ruido de corriente ultrabaja y amplificadores de voltaje compensado, AD8676 y AD8599, se utilizan para construir un filtro activo y un circuito sumador. Se utiliza un SPDT dual de riel a riel, 0,8 Ω máx., de suministro único, el ADG854, para convertir y seleccionar la señal SIN/COS, que luego se envía al módulo de captura de datos.
Todo el sistema del simulador de soluciones está alimentado por un adaptador externo de 12 V con diferentes niveles de voltaje generados mediante convertidores de CC a CC y controladores LDO. En la Figura 9 se muestra una cadena de señal de potencia detallada. El ADP5071 genera voltajes positivos y negativos de 16 V, pero se pueden generar voltajes positivos y negativos de 15 V más claros y estables utilizando el ADP7118 y el ADP7182. Estas fuentes de alimentación se utilizan principalmente para alimentar los circuitos asociados con el DAC. De manera similar, se generan potencias claras y estables de +3,3 V, +5 V, –5 V y –2 V utilizando ADP2300, ADP7118, ADM660 y AD7182. Estos poderes se utilizan principalmente para alimentar circuitos relacionados con CAN y requisitos de diseño detallados.
Banco de pruebas y resultado del simulador de soluciones
El banco de pruebas del sistema completo se muestra en la Figura 10. Contiene una placa simuladora de solucionador, una placa de evaluación AD2S1210 y una GUI. La imagen de la GUI y el banco de pruebas se muestra en la Figura 11. La GUI de AD2S1210 se usa para evaluar directamente el rendimiento del simulador de solución, especialmente la velocidad y el rendimiento angular. A través de la GUI del Resolver Simulator, se pueden configurar la velocidad, el rendimiento angular y la señal de falla.
La Figura 12 muestra el rendimiento angular y de velocidad INL de un AD2S1210 de 16 bits con el modo de histéresis desactivado.
En comparación con los dispositivos de simulación de solver estándar, el rendimiento de esta solución se puede ver en la Tabla 2. Se puede lograr una precisión angular de 0,006° en un equipo de prueba real, con una precisión teórica de 0,0004° cuando se prueba. velocidad máxima de salida de 3000 rps, precisión de velocidad de 0,004 rps, y puede acomodar fácilmente el AD2S1210 en modo de 10 bits a aproximadamente 16 bits.
| Producto/Parámetro | Atlántico Norte 5330A | Atlántico Norte 5300A | Esta solución | AD2S1210 Requerido |
| Frecuencia de excitación | 47Hz a 10kHz | 360Hz a 20kHz | 2kHz a 20kHz | 2kHz a 20kHz |
| Precisión angular | De 0,003° a ~0,015° | De 0,00055556° a ~0,0167° | Mejor que 0,006° en Carrier 12,2070 kHz | 0,0417° y 1 LSB |
| rango de tarifas | Hasta 277 rps | Hasta 278 rps | Hasta 3000 rps | Hasta 2500 rpm a 8,19 MHz de reloj |
| Tasa de precisión | ±1% | 0,004 rpm (<150 rpm) | ±0,0305 rpm (<125 rpm) | |
La Tabla 3 muestra el modo de falla admitido en este simulador. Para fallas relacionadas con la fase, un rango de 0° a aproximadamente 360° puede soportar una señal SIN/COS. Para fallas relacionadas con la amplitud, un rango de 0 V a alrededor de 5 V puede soportar la señal SIN/COS. El exceso de velocidad, IGBT, desconexión y otras fallas también se pueden simular con esta solución.
| Modo por defecto | cambio de grado | cambio de grado | Desajuste de amplitud | La amplitud fue excedida | perturbaciones IGBT | Perturbación aleatoria | Más que velocidad | Corto |
| Intervalo | 0° a ~360° | 0° a ~360° | 0V a ~5V | 0V a ~5V | ✓ | ✓ | 0 rps a ~ 3000 rps | ✓ |
Para la falla de IGBT, se muestra una prueba de ejemplo en la Figura 13. Configure la salida del simulador a 45°, luego agregue una señal de interferencia periódica a la salida SIN/COS. Como se muestra en la GUI de velocidad y rendimiento angular de la placa de evaluación AD2S1210, el rendimiento angular fluctuará alrededor de 45°, mientras que al mismo tiempo la velocidad fluctuará alrededor de 0 rps.
Conclusión
Aunque la mayoría de las aplicaciones relacionadas con CDR son interferencias, se pueden inducir muchos tipos de fallas en condiciones extremas. Cuando construya su propio simulador de solución, siga esta solución, ya que puede ayudarlo no solo a evaluar el rendimiento de su sistema bajo interferencia, sino también a calibrar y verificar sus productos como lo hace un simulador normal. El análisis detallado de errores es muy útil para comprender por qué se necesitan señales analógicas SIN/COS de precisión, y todos los tipos de fallas discutidas en el artículo pueden simularse para ayudar a la verificación de seguridad funcional.
Referencias
Chicos, Geoffrey. msgstr "Sincronización y conversión de resolución." Dispositivos analógicos, Inc., 1980.
Hanselman, Duane C.Requisitos de señal de resolución para conversión de resolución a digital de alta precisión.” IEEE Trans.Ind. Electrón., vol. 37, núm. 6 de diciembre de 1990.
Lynch, Michael. msgstr "Fuente de voltaje de alta precisión". Dispositivos analógicos, Inc., octubre de 2017.
Oh Meara, Shane. Kit de evaluación AD7380. Dispositivos analógicos, Inc., 2019.
Symczak, Jakub, Shane O'Meara, Johnny Gealon y Christopher Nelson De La Rama "El convertidor de resolución precisa a digital mide la posición angular y la velocidad". Dispositivos analógicos, Inc., marzo de 2014.
Gracias
Muchas gracias al pasante de ADI Edward Luo y a los ingenieros de aplicaciones Shane O'Meara, Steven Xie, Karl Wei y Michael Lynch por su orientación y apoyo en los esfuerzos de diseño y prueba necesarios para este artículo.
Si quieres conocer otros artículos parecidos a Sistema simulador de solución de alta precisión con función de inyección de fallas puedes visitar la categoría Generalidades.
Deja una respuesta














¡Más Contenido!