¿Qué es la transformada de Laplace? Fórmula, propiedades, condiciones y aplicaciones
Las matemáticas desempeñan un papel decisivo en la comprensión del comportamiento y el funcionamiento de eléctrico e sistemas electrónicos. Los polinomios, el álgebra, la probabilidad, la integración y la diferenciación, etc., forman una parte importante de las herramientas utilizadas para resolver sistemas. Con la creciente complejidad de los sistemas, se necesitan métodos muy sofisticados. Las ecuaciones diferenciales se utilizan ampliamente para definir los sistemas de control. Estas ecuaciones son sencillas de resolver. Pero la complejidad surge al resolver ecuaciones diferenciales de orden superior. Para resolver estas complejas ecuaciones diferenciales de orden superior, el método matemático que ha resultado eficaz es Transformación de Laplace. Como esta transformación se utiliza mucho, es útil saber para qué se utiliza y cómo funciona.
¿Qué es una transformada de Laplace?
En matemáticas, las transformaciones se aplican para transformar una variable de una forma a otra para que la ecuación sea más fácil de manejar. La transformada de Laplace hace prácticamente lo mismo. Transforma una ecuación diferencial de orden superior en una forma polinómica que es mucho más sencilla que resolver la ecuación diferencial directamente.
Pero hay diferentes transformaciones, como la transformada de Fourier y la transformada z. ¿Qué hace especial a la transformada de Laplace? La principal ventaja de la transformada de Laplace es que se define tanto para sistemas estables como inestables, mientras que la transformada de Fourier sólo se define para sistemas estables.
Fórmula de la transformada de Laplace
La transformada de Laplace de una función f
La ecuación anterior se toma como un lado Ecuación de la transformación de Laplace. Cuando los límites se extienden a todo el eje real, entonces la ecuación de Transformada bilateral de Laplace puede definirse como
En circuitos prácticos como Circuitos RC y RL normalmente se utilizan condiciones iniciales, por lo que se aplica la transformada de Laplace unilateral para el análisis.
Como s= σ + jω, cuando σ = 0 la transformada de Laplace se comporta como la transformada de Fourier.

Condiciones de aplicabilidad de la transformada de Laplace
Las transformadas de Laplace se llaman transformadas integrales, por lo que existen condiciones necesarias para la convergencia de estas transformadas.
es decir, f debe ser localmente integrable para el intervalo[0, ∞]y, dependiendo de si σ es positivo o negativo, e^(-σt) puede ser decreciente o creciente. En las transformadas de Laplace de dos caras, en lugar de un único valor, la integral converge a un determinado intervalo de valores conocido como región de convergencia.
Propiedades de la transformada de Laplace:
Linealidad
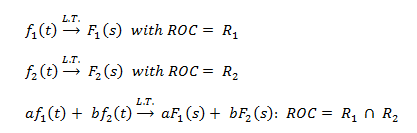
Desplazamiento temporal
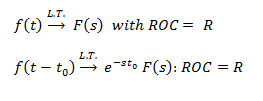
Desplazamiento en el dominio S

Inversión del tiempo
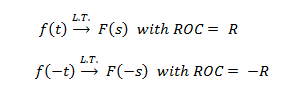
Diferenciación en el dominio S
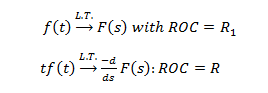
Convolución en el tiempo

Teorema del valor inicial
El teorema del valor inicial se aplica cuando en la transformación de Laplace el grado del numerador es menor que el grado del denominador
Teorema del valor final
Si todos los polos de sF(s) se encuentran en la mitad izquierda del plano S, se aplica el teorema del valor final.
 Transformación inversa de Laplace
Transformación inversa de Laplace
Debido a la característica de convergencia, la transformada de Laplace también tiene una transformada inversa. Las transformadas de Laplace presentan un mapeo uno a uno de un espacio de funciones a otro. La fórmula de la transformada inversa de Laplace es
¿Cómo calcular la transformada de Laplace?
La transformada de Laplace facilita el manejo de las ecuaciones. Cuando se da una ecuación diferencial de orden superior, se aplica la transformada de Laplace, que convierte la ecuación en una ecuación algebraica, lo que facilita su manejo. Las raíces se calculan entonces simplificando esta ecuación algebraica. En este punto, se encuentra la transformada inversa de Laplace de la expresión más sencilla, que resuelve la ecuación diferencial de orden superior.

Aplicaciones de la transformada de Laplace
- Análisis de sistemas eléctricos y circuitos electrónicos.
- Descomposición de ecuaciones diferenciales complejas en formas polinómicas más sencillas.
- La transformada de Laplace proporciona información sobre los estados estacionarios y transitorios.
- En el aprendizaje automático, la transformada de Laplace se utiliza para hacer predicciones y análisis en la minería de datos.
- La transformada de Laplace simplifica los cálculos en la modelización de sistemas.
Aplicación de la transformada de Laplace en el procesamiento de señales
Las transformadas de Laplace se utilizan a menudo en el procesamiento de señales. Junto con la transformada de Fourier, la Transformación de Laplace se utiliza para estudiar las señales en el dominio de la frecuencia. Cuando hay frecuencias pequeñas en la señal en el dominio de la frecuencia, cabe esperar que la señal sea homogénea en el dominio del tiempo. El filtrado de una señal suele realizarse en el dominio de la frecuencia y Laplace es una herramienta importante para convertir una señal del dominio del tiempo al dominio de la frecuencia.
Aplicación de la transformada de Laplace en los sistemas de control
Los sistemas de control suelen estar diseñados para controlar el comportamiento de otros dispositivos. Ejemplo de sistemas de control puede ir desde un simple controlador de calefacción doméstica hasta un sistema de control industrial que regule el comportamiento de la maquinaria.
Normalmente, los ingenieros de control utilizan ecuaciones diferenciales para describir el comportamiento de varios bloques funcionales de bucle cerrado. La transformada de Laplace se utiliza para resolver estas ecuaciones sin perder la información crucial de las variables.
Caracterización de sistemas lineales invariantes en el tiempo mediante la transformada de Laplace
Para un sistema aleatorio el ROC asociado al sistema, la función es el semiplano derecho. Un sistema es antirreglamentario si su respuesta al impulso h
Si la ROC de las funciones del sistema H(s) incluye el eje jω, se dice que la L.T.I. del sistema es estable. Si un sistema aleatorio con funciones de sistema racionales H(s) tiene partes reales negativas para todos sus polos, entonces el sistema es estable.
La transformada de Laplace es, pues, una herramienta fundamental para el análisis de circuitos. Podemos decir que, como el estetoscopio es para el médico, la transformada de Laplace es para el ingeniero de control. ¿Cómo se considera la transformada de Laplace? ¿Cómo te han sido útiles?
Si quieres conocer otros artículos parecidos a ¿Qué es la transformada de Laplace? Fórmula, propiedades, condiciones y aplicaciones puedes visitar la categoría Generalidades.
Deja una respuesta

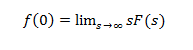
¡Más Contenido!