¿Qué es Fermi Dirac Distribución? Diagrama de bandas de energía y aproximación de Boltzmann
electrones y agujeros juegan un papel esencial en la transferencia de electricidad en los semiconductores. Estas partículas están dispuestas en un nivel de energía diferente en un semiconductor. El movimiento de electrones de un nivel de energía a otro genera electricidad. Un electrón dentro del metal debe poseer un nivel de energía al menos más alto que la energía de la barrera superficial para escapar a un nivel de energía más alto.
Se han propuesto y aceptado muchas tesis que explican las características y el comportamiento de los electrones. Pero ciertos comportamientos del electrón, como la independencia de la corriente de emisión de la temperatura, etc., seguían siendo un misterio. Entonces un avance estadístico, Estadísticas de Fermi Diracpublicado por Enrico Fermi y Pablo Dirac en 1926 ayudó a resolver estos rompecabezas.
Desde allí Desglose de Fermi Dirac se aplica para explicar el colapso de una estrella a una enana blanca, para explicar la emisión de electrones libres de los metales, etc….
Desglose de Fermi Dirac
Antes de entrar en el Función de distribución de Fermi Dirac veamos la distribución de energía de los electrones en varios tipos de semiconductores. La energía máxima que puede tener un electrón libre en un material a temperatura absoluta, es decir, 0k, se denomina nivel de energía de Fermi. El valor de la energía de Fermi varía según los materiales. Según la energía que poseen los electrones en un semiconductor, los electrones se organizan en tres bandas de energía: banda de conducción, nivel de energía de Fermi, banda de valencia.
Mientras que la banda de conducción contiene electrones excitados, la banda de valencia contiene huecos. Pero, ¿para qué sirve el nivel de Fermi? El nivel de Fermi es el estado de energía que tiene ½ probabilidad de ser ocupado por un electrón. En pocas palabras, es el máximo nivel de energía que puede tener un electrón a 0k y la probabilidad de encontrar el electrón por encima de este nivel a temperatura absoluta es 0. A temperatura de cero absoluto, la mitad del nivel de Fermi estará lleno de electrones.
En el diagrama de banda de energía del semiconductor, el nivel de Fermi se encuentra en el medio de la banda de conducción y valencia para un semiconductor intrínseco. Para semiconductores extrínsecos, el nivel de Fermi se encuentra cerca de la banda de valencia en Semiconductor tipo P y para semiconductor tipo nestá cerca de la banda de conducción.
Se anota el nivel de energía de Fermi miF, se nota la banda de conducción micontra y la banda de valencia se denota EV.
Nivel de Fermi en semiconductores de tipo N y P
Función de distribución de Fermi Dirac
La probabilidad de que el estado de energía disponible 'E' esté ocupado por un electrón a temperatura absoluta T en condiciones de equilibrio térmico viene dada por la función de Fermi-Dirac. De la física cuántica, la expresión de distribución de Fermi-Dirac es
Donde k es la constante de Boltzmann en OkT es la temperatura en 0k y miF es el nivel de energía de Fermi en eV.k= 1.38X10-23 J/K
El nivel de Fermi representa el estado de energía con un 50% de probabilidad de llenarse si no existe banda prohibida, es decir, si mi = miFentonces f(E)=1/2 para cualquier valor de temperatura.
La distribución de Fermi-Dirac solo da la probabilidad de ocupación del estado en un nivel de energía dado, pero no proporciona ninguna información sobre el número de estados disponibles en ese nivel de energía.
Distribución de Fermi Dirac y diagrama de bandas de energía

El gráfico anterior muestra el comportamiento del nivel de Fermi en diferentes rangos de temperatura T= 00K, T= 3000K, T= 25000k A T=0Kla curva tiene características de escalón.
A t = 00kel número total de niveles de energía ocupados por electrones se puede conocer utilizando la función de Fermi-Dirac.
Para un nivel de energía dado mi > miFel término exponencial en la función de Fermi-Dirac se convierte en 0 y lo que significa que la probabilidad de encontrar el nivel de energía ocupado mayor que miFes cero
Para un nivel de energía dado mi < miF cuyo valor significa que todos los niveles de energía con energía están por debajo del nivel E de FermiF estará ocupado t = 00k. Esto indica que el nivel de energía de Fermi es la energía máxima que puede tener un electrón a temperatura cero absoluta.
Para una temperatura superior a la temperatura absoluta y mi = miFindependiente del valor de la temperatura.
Para una temperatura superior a la temperatura absoluta y mi < miFentonces la exponencial será negativa. f(mi) comienza en 0,5 y tiende a aumentar hacia 1 a medida que E disminuye.
Para una temperatura superior a la temperatura absoluta y mi > miFla exponencial será positiva y creciente con E. f(E) parte de 0,5 y tiende a decrecer hacia 0 cuando E aumenta.
Distribución de Fermi Dirac Aproximación de Boltzmann
La distribución de Maxwell-Boltzmann es la distribución comúnmente utilizada Aproximación de la distribución de Fermi Dirac.
La distribución de Fermi-Dirac está dada por
Usando la aproximación de Maxwell-Boltzmann, la ecuación anterior se reduce a
Cuando la diferencia entre la energía del portador y el nivel de Fermi es grande en comparación con, el término 1 en el denominador puede despreciarse. Para la aplicación de la distribución de Fermi-Dirac, el electrón debe seguir el principio exclusivo de Pauli, que es importante en casos de alto dopaje. Pero la distribución de Maxwell-Boltzmann ignora este principio, por lo que la aproximación de Maxwell-Boltzmann se limita a casos ligeramente dopados.
Estadísticas de Fermi Dirac y Bose-Einstein
La estadística de Fermi-Dirac es la rama de la estadística cuántica, que describe la distribución de partículas en estados de energía que contienen partículas idénticas que obedecen al principio de exclusión de Pauli. Dado que las estadísticas de FD se aplican a partículas con espín semientero, se denominan fermiones.
Un sistema que consta de partículas termodinámicamente en equilibrio e idénticas, en el estado de una sola partícula I, el número promedio de fermiones viene dado por la distribución FD como
¿Dónde está el estado de una sola partícula? yoel potencial químico total se denota por, kB es la constante de Boltzmann mientras que j es la temperatura absoluta.
Las estadísticas de Bose-Einstein son lo opuesto a las estadísticas de FD. Esto se aplica a partículas con espín entero completo o sin espín, llamadas bosones. Estas partículas no obedecen al principio de exclusión de Pauli, lo que significa que una misma configuración cuántica puede estar llena de más de un bosón.
Las estadísticas FD y las estadísticas de Bore-Einstein se aplican cuando el efecto cuántico es grande y las partículas son indistinguibles.
Problema de distribución de Fermi Dirac
En un sólido, considere el nivel de energía ubicado 0.11 eV por debajo del nivel de Fermi. ¿Encuentre la probabilidad de que este nivel no esté ocupado por el electrón?

Se trata de Desglose de Fermi Dirac. Finalmente, a partir de la información anterior, podemos concluir que las propiedades macroscópicas de un sistema se pueden calcular utilizando una función de Fermi-Dirac. Se utiliza para conocer la energía de Fermi en casos de temperatura cero y finita. Respondamos una pregunta sin ningún cálculo, basándonos en nuestra comprensión de la distribución de Fermi-Dirac. Para un nivel de energía E, 0,25 eV por debajo del nivel de Fermi y una temperatura por encima de la temperatura absoluta, ¿la curva de distribución de Fermi disminuye hacia 0 o aumenta hacia 1?
Si quieres conocer otros artículos parecidos a ¿Qué es Fermi Dirac Distribución? Diagrama de bandas de energía y aproximación de Boltzmann puedes visitar la categoría Generalidades.
Deja una respuesta

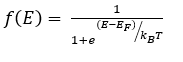


¡Más Contenido!