Qué es el teorema de Tellegen: cómo funciona y sus aplicaciones
En el análisis de redes, conocer el teorema de la red es muy importante para el análisis de circuitos. Entonces, hay diferentes teoremas de red disponibles como superposición, teorema de Tellegen, Norton, máxima transferencia de potencia, teorema de Thevenin, compensación, sustitución, reciprocidad, teorema de Millman y Miller. Pero comprender cada teorema de red es muy importante porque cada teorema se usa para aplicaciones específicas. Este artículo analiza uno de los tipos de teoremas de celosía como teorema de Tellegentrabajar con ejemplos.
¿Qué es el teorema de Tellegen?
El teorema de Tellegen es un tipo de teorema de red que fue inventado y publicado por un ingeniero eléctrico holandés llamado Bernard DH Tellegen en 1952. En el análisis de redes, este teorema es muy esencial en comparación con otros teoremas porque la mayoría de los teoremas de celosía se pueden deducir usando este teorema.
Este teorema de la red depende principalmente de la ley de Kirchhoff. Por lo tanto, este teorema se puede aplicar simplemente a la red que sigue la ley de Kirchhoff. Este teorema de la red se usa en circuitos que tienen elementos lineales, no lineales, activos, pasivos, variables en el tiempo o invariables.
El enunciado del teorema de Tellegen es: "la suma de la potencia directa utilizada por diferentes elementos en diferentes ramas es igual a cero (0) para cualquier tipo de red". Este teorema funciona según el principio del principio de conservación de la energía, por lo que se utiliza en aplicaciones biológicas y químicas para descubrir el rendimiento activo de la red física y también se utiliza para diseñar filtros en el procesamiento de señales.
Pasos para resolver el teorema de Telegen
Se deben seguir los siguientes pasos para resolver cualquier red eléctrica usando el teorema de Tellegen.
- Primero, necesitamos ubicar las caídas de tensión en las ramas de una red eléctrica.
- Encuentre corrientes de rama equivalentes usando técnicas de análisis convencionales
- Entonces este teorema se puede justificar sumando los productos de voltajes y corrientes en todas las ramas.
Teorema de Tellegen para circuitos de corriente alterna
El concepto básico del teorema de Tellegen es ser el mismo en circuitos de CA o CC. Para la aplicación del circuito de CA, se puede decir que en cualquier salida de red variable en el tiempo, activa o pasiva, lineal o no lineal, por fuentes de CA, la suma de la potencia instantánea o compleja de la fuente es cero.
Para el análisis de este teorema, considere la red con 'n' número de elementos. La corriente instantánea que fluye en el elemento es i1, i2, i3,i4…., mientras que la tensión instantánea en esta rama es v1, v2, v3,v4…., vn.
Entonces, la corriente y el voltaje instantáneos para el elemento 1 son i1 y v1 y la potencia instantánea (p1) utilizada a través de este elemento es 'v1i1'.
p1 = v1* i1
Para el elemento 2, la potencia instantánea (p2) es
p2 = v2* i2
De manera similar, la potencia instantánea del n-ésimo elemento es (pn) es
pn = vn* en
Basado en el teorema de Tellegen, cualquier suma de potencia instantánea es '0'. Así que tenemos que sumar todas las potencias instantáneas como p1, p2, p3, p4…., on.
p1 + p2 + p3 +p4 … + pn = 0
v1 i1+ v2 i2 + v3 i3 + v4i4… + vn en = 0
La ecuación anterior se puede escribir en forma general para la k-ésima rama como;
En la ecuación anterior,
'n' es el número total de sucursales dentro de la red
'vk' es un voltaje instantáneo de la rama 'kth'
'ik' es una corriente de rama instantánea 'kth'
'pk' es una potencia instantánea de la rama 'kth'
Si consideramos la siguiente figura como una rama AB equivalente a la rama ak.
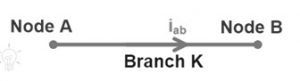
Por tanto, la tensión instantánea vk = va – vb
El flujo de corriente instantáneo en la rama aab es 'ik';
ik=iab
En consecuencia, la potencia instantánea como pk es;
pk = vk* ik = (va – vb) iab …..(I)
Ahora tenemos que considerar la corriente instantánea en la dirección opuesta de b a a;
iab = – iab
Voltaje instantáneo;
vk = vb – ir
La potencia instantánea 'pk' es;
pk = vk ik = (vb – va) iba ……(ii)
Sumando las ecuaciones i y ii anteriores, podemos obtener
2vk ik = (va – vb) iab + (vb – va) iba
vk ik = 1/2 [(va – vb) iab + (vb – va) iba] ……..(iii)
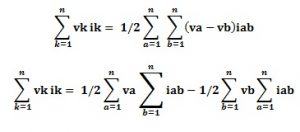
Según la ley de corriente de Kirchhoff, la suma algebraica de la corriente es cero en un nodo del circuito.
De este modo,
Si sustituimos este valor en la ecuación anterior (iv), obtenemos
Así, se verifica que la suma de las potencias entregadas a la red es '0'. Por lo tanto, se demuestra el teorema de Tellegen. También se explica que la suma de las potencias absorbidas a través de los elementos de la red es equivalente a la suma de las potencias entregadas a través de las fuentes.
Problemas resueltos por el teorema de Tellegen
Los problemas de ejemplo del teorema de Tellegen se resuelven a continuación.
Ejemplo 1: Compruebe el teorema de Telegen para la siguiente red de CC.
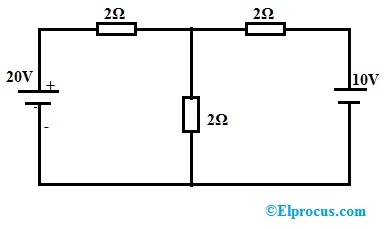
Aplicar KCL al nodo
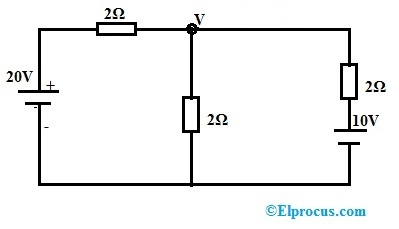
V-20/2+V/2+V-10/2 = 0
(V-20+V+V-10)/2 =0
3V=30
V = 30/3 = 10 voltios
Cuando la corriente fluye a través del circuito, entonces
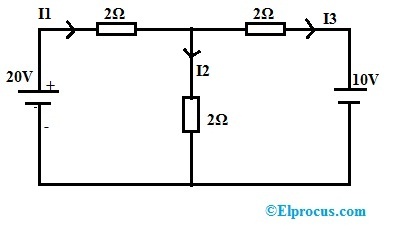
I1 = 20-V/2 = 20-10/2 =10/2 = 5A
I2 = V/2 = 10/2 = 5A
I3 = V-10/2 = 10-10/2 = 0
La potencia suministrada por la fuente de 20V es,

P = V x I => 20×5 = 100 vatios
La potencia absorbida por los elementos pasivos de la red es
P = i^2 R => 5^2×2+ 5^2×2
25x2 + 25x2 = 100 vatios
Entonces potencia suministrada = potencia absorbida
Así, la suma algebraica de todas las potencias de una red es igual a cero.
Ejemplo2:
Usando el teorema de Tellegen, encuentre el voltaje a través de la fuente de corriente de 6A para el siguiente circuito.
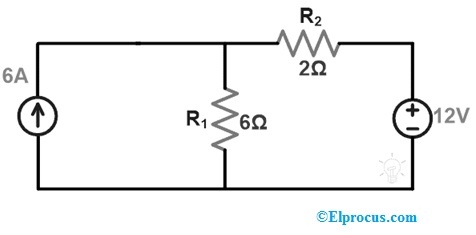
Primero, necesitamos calcular la corriente o el voltaje que fluye en el circuito aplicando KVL o KCL a la red anterior.
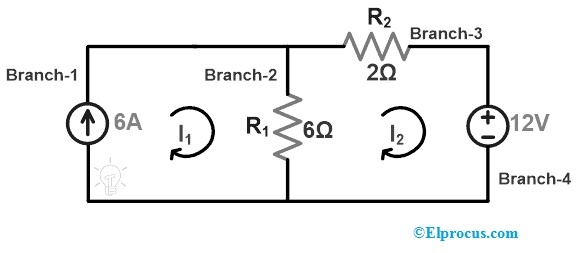
Al aplicar KVL al loop-2 podemos obtener
-12 = 8I2 – 6I1
El flujo de corriente en todo el ramal, incluida la fuente de corriente, es I1 = 6A;
Sustituya este valor 'I1' en la ecuación anterior; podemos obtener el valor 'I2'.
-12 = 8I2 – 6I1
Sabemos que I1 = 6A
-12 = 8I2 – 6(6)
-12 = 8I2 – 36
8I2 = 36 – 12 => 24
I2 = 3A
El flujo de corriente en la rama 2 es;
I12 = I1 – I2 => 6 – 3 = 3A
I12 = 3A
Ahora necesitamos encontrar la potencia para cada rama.
P1 = V I1 = V x 6 = 6 x V
P2 = R1 I12^2 = 6x9 = 54W
P3 = R2 I2^2 = 2x9 = 18W
P4 = V I2 = -12 x 3 = -36W
Aquí las fuentes de energía están disponibles en dos ramas. Por lo tanto, estas ramas pueden considerarse como ramas que entregan energía. Establezca el signo positivo (+ve) en la potencia instantánea.
Las ramas restantes solo tienen resistencias. Por lo tanto, son ramas que absorben el potencia y poner el signo negativo (-) a la potencia instantánea.
Las potencias como P1 y P4 tienen signo positivo, mientras que las potencias P2 y P3 tienen signo negativo.
Ahora tenemos que sumar toda la potencia instantánea.
P1 – P2 – P3 + P4 = 0W
P1-54-18 + 36 = 108W
La potencia transmitida a través de la fuente de corriente de 6A es de 108W. Por lo tanto, el voltaje a través de la fuente de corriente 6A puede calcularse usando la siguiente ecuación.
P1 = VI
108W=Vx6A
V=108/6=18V
Por lo tanto, el voltaje a través de la fuente de corriente de 6A es de 18V.
¿Cómo se relacionan KCL KVL y el teorema de Tellegen?
La consecuencia de las leyes de Kirchhoff como KVL y KCL es el teorema de Tellegen. Este teorema se verifica mediante KVL o KCL.
¿Podemos verificar el teorema de Thevenin en circuitos de CA y CC?
Sí, podemos verificar el teorema de Thevenin en circuitos de CA y CC. Similar a los circuitos de CC, este teorema se puede aplicar a los circuitos de CA que contienen elementos lineales como resistencias, capacitores e inductores. Similar a la resistencia de Thevenin equivalente, se puede obtener una impedancia equivalente cambiando todas las fuentes de voltaje por sus impedancias internas.
¿Qué teorema se aplica a los circuitos lineales y no lineales?
El teorema de sustitución se aplica a circuitos lineales y no lineales
¿Cómo usar el teorema de Tellegen?
El teorema de Tellegen se puede utilizar para diseñar filtros y sistemas operativos complejos.
Aplicaciones
los aplicaciones del teorema de Tellegen Incluya lo siguiente.
- El teorema de Tellegen se utiliza para examinar sistemas de redes difíciles como circuitos eléctricos, redes metabólicas y biológicas, procesos químicos y redes de transporte por tuberías.
- El teorema de Tellegen se utiliza para diseñar filtros en el sistema de procesamiento de señales digitales (DSP).
- Utilizado en procesos biológicos y químicos.
- Se utiliza en el análisis y la topología de la estructura de la red de reacción.
- Utilizado en diferentes plantas químicas y de petróleo para determinar la estabilidad del sistema complejo.
- Este teorema es aplicable a circuitos que tienen elementos lineales/no lineales, variables en el tiempo/no variables y activos/pasivos.
Así, se trata de una descripción general del teorema de Tellegen, derivación, ejemplos de problemas y sus aplicaciones. Las limitaciones del teorema de Tellegen son que para la verificación del teorema de Tellegen se utilizan las ecuaciones KVL y KCL. Este teorema trabaja principalmente sobre la ley del principio de conservación de la energía. Este teorema se utiliza en varios sistemas de red. Aquí hay una pregunta para ti. ¿Qué es el teorema de la superposición?
Si quieres conocer otros artículos parecidos a Qué es el teorema de Tellegen: cómo funciona y sus aplicaciones puedes visitar la categoría Generalidades.
Deja una respuesta



¡Más Contenido!