Multiplicadores vs Moduladores | Dispositivos analógicos
Aunque muchas descripciones de la modulación la describen como un proceso de multiplicación, la verdad es un poco más compleja.
Primero, para ser bastante claro, si las dos entradas de un perfecto multiplicador alimentados con una señal, Acos(ωt), y una portadora no modulada, cos(ωt), tendríamos una modulador. Esto sucede porque las dos formas de onda periódicas, Asporque (ohst) y ACporque (ohCt), aplicado a las entradas de un multiplicador (con un factor de escala de 1 V para simplificar el análisis), produce una salida dada por:
Vo
Si el transportista, ACporque (ohCt), tiene una amplitud de 1 V (AC = 1), esto se simplifica aún más a:
Vo
Pero, en la mayoría de los casos, un modulador es un mejor circuito para realizar esta función. Un modulador (también llamado mezclador cuando se utiliza como variador de frecuencia) está estrechamente relacionado con un multiplicador. La salida de un multiplicador es el producto instantáneo de sus entradas. La salida de un modulador es el producto instantáneo de la señal en una de sus entradas (conocida como la señal entrada) y el signo de la señal en la otra entrada (conocida como transportador aporte). La figura 1 muestra dos formas de modelar la función de modulación: como un amplificador cuya ganancia se cambia entre positiva y negativa por la salida de un comparador en su entrada portadora, o como un multiplicador con un amplificador limitador de alta ganancia entre la entrada portadora y una de ellas. sus puertos. Ambas arquitecturas se han utilizado para producir moduladores, pero la versión de amplificador conmutado (utilizada en el modulador balanceado AD630) tiende a ser más lenta. La mayoría de los moduladores de circuitos integrados de alta velocidad constan de un multiplicador translineal (basado en la celda de Gilbert) con un amplificador limitador en la ruta de la portadora que satura una de las entradas. Este amplificador limitador puede proporcionar una alta ganancia, lo que permite una entrada de portadora de bajo nivel, o una baja ganancia y características de limitación limpias, lo que requiere una entrada de portadora comparativamente grande para un funcionamiento correcto. Consulte la hoja de datos para obtener información específica.
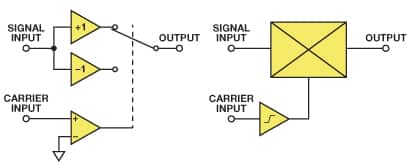
Usamos moduladores en lugar de multiplicadores por varias razones. Ambos puertos de un multiplicador son lineales, por lo que cualquier ruido o modulación en la entrada de la portadora multiplica la entrada de la señal y degrada la salida, mientras que la variación de amplitud en la entrada de la portadora de un modulador puede ignorarse en su mayoría. Los mecanismos de segundo orden pueden hacer que el ruido de amplitud en la entrada de la portadora afecte la salida, pero estos se minimizan en los mejores moduladores y no se discutirán aquí. Un modelo simple de un modulador utiliza interruptores accionados por la portadora. Un interruptor abierto (perfecto) tiene resistencia infinita y corriente de ruido térmico cero, y un interruptor cerrado (perfecto) tiene resistencia cero y voltaje de ruido térmico cero, por lo que los moduladores, aunque sus interruptores no sean perfectos, tienden a tener menos ruido interno que multiplicadores Además, es más fácil diseñar y fabricar un modulador de alta frecuencia y alto rendimiento que un multiplicador similar.
Al igual que los multiplicadores analógicos, los moduladores multiplican dos señales pero, a diferencia de los multiplicadores analógicos, la multiplicación no es lineal. En cambio, la señal de entrada se multiplica por +1 cuando la polaridad de la entrada de la portadora es positiva y por –1 cuando es negativa. En otras palabras, la señal se multiplica por una onda cuadrada en la frecuencia portadora.
Una onda cuadrada con una frecuencia de ωCPuede representarse mediante la serie de Fourier de armónicos impares:
k[cos(ωct) – 1/3cos(3ωct) + 1/5cos(5ωct) – 1/7cos(7ωct) + …]
La suma de la serie: [+1, –1/3, +1/5, –1/7 + ...] es π/4. Por lo tanto, el valor de K es 4/π, de modo que un modulador balanceado actúa como un amplificador de ganancia unitaria cuando se aplica una señal de CC positiva a su entrada portadora.
La amplitud de la portadora no es importante siempre que sea lo suficientemente grande como para impulsar el amplificador limitador, por lo que un modulador impulsado por una señal, Asporque (ohst), y un portador, cos(ωCt), producirá una salida que es el producto de la señal y la portadora al cuadrado:
2A/p[cos(ωs + ωc)t + cos(ωs – ωc)t –
1/3{cos(ωs + 3ωc)t + cos(ωs – 3ωc)t} +
1/5{cos(ωs + 5ωc)t + cos(ωs – 5ωc)t} –
1/7{cos(ωs + 7ωc)t + cos(ωs – 7ωc)t} + …]
Esta salida contiene las frecuencias de suma y diferencia de la señal y la portadora, y de la señal y cada uno de los armónicos impares de la portadora. En un modulador ideal, perfectamente balanceado, los productos de armónicos pares no están presentes. Sin embargo, en un modulador real, las compensaciones residuales en el puerto de la portadora dan como resultado productos armónicos uniformes de bajo nivel. En muchas aplicaciones, un filtro de paso bajo (LPF) elimina los productos de los armónicos más altos. Recuerda que cos(A) = cos(–A), entonces cos(ωmetro - NoC)t = cos(NωC - Ohmetro)t, y no tenemos que preocuparnos por las frecuencias "negativas". Después del filtrado, la salida del modulador viene dada por:
2A/p[cos(ωs + ωc)t + cos(ωs – ωc)t]
Esta es la misma expresión que la salida de un multiplicador, excepto por una ganancia ligeramente diferente. En los sistemas prácticos, la ganancia se normaliza mediante amplificadores o atenuadores, por lo que aquí no consideraremos las ganancias teóricas de varios sistemas.
En casos simples, obviamente es mejor usar un modulador que un multiplicador, pero ¿cómo definimos simple? Cuando se utiliza un modulador como mezclador, las entradas de la señal y la portadora son ondas sinusoidales simples a frecuencias f1 y fCy la salida sin filtrar contiene la suma (F1 + FC) y diferencia (F1 – Fc) frecuencias, más la suma y diferencia de frecuencias de la señal y los armónicos impares de la portadora (F1 + 3FC), (F1 – 3FC), (F1 + 5FC), (F1 – 5FC), (F1 + 7FC), (F1 – 7FC)… Después del LPF, esperamos encontrar solo los productos fundamentales, (F1 +FC) y (F1 –FC).
Si (F1 + FC) > (F1 – 3FC), no será posible separar los productos fundamental y armónico con un LPF simple, sin embargo, porque uno de los productos armónicos está a una frecuencia más baja que uno de los productos fundamentales. Este no es un caso simple, por lo que se necesita más análisis.
Si asumimos que la señal contiene una sola frecuencia, F1o una señal más compleja que se propaga a través de la banda desde F1 a F2, podemos analizar el espectro de salida de nuestro modulador, como se muestra en los siguientes diagramas. Suponga un modulador perfectamente balanceado sin fuga de señal, fuga de portadora o distorsión, de modo que los productos de entrada, portadora y espurios no aparezcan en la salida. Las entradas se muestran en negro (o en gris pálido en los diagramas de salida, aunque en realidad no esté presente).
La figura 2 muestra las entradas: una señal en el F1 a F2 banda y un portador en FC. Un multiplicador no tendrá armónicos de portador impares en 1/3(3FC), 1/5(5FC), 1/7(7FC)…, mostrado como líneas de puntos para el modulador. Tenga en cuenta que las fracciones 1/3, 1/5 y 1/7 se refieren a las amplitudes, no a las frecuencias.

La Figura 3 muestra la salida de un multiplicador, o un modulador, y LPF con una frecuencia de corte de 2FC.
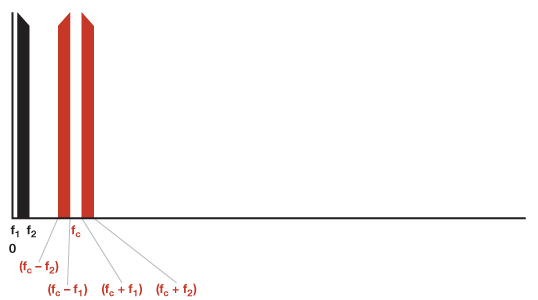
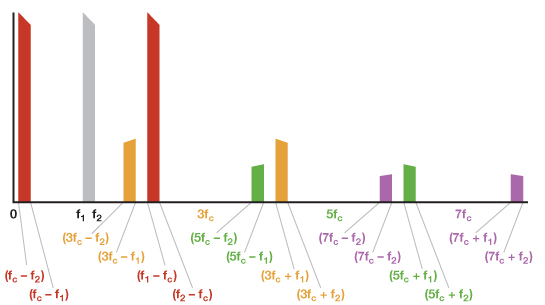
La figura 4 muestra la salida de un modulador sin filtrar (pero no los productos armónicos por encima de 7FC).
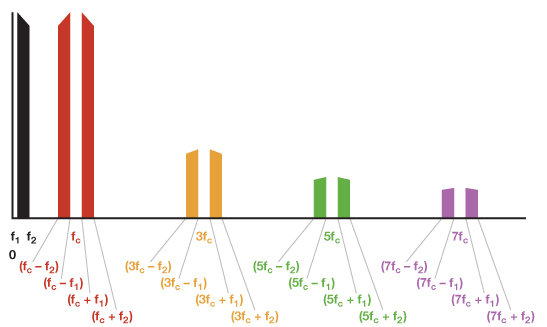
Si la banda de señal, F1 a F2se encuentra dentro de la banda de Nyquist (dc a FC/2), un LPF con corte por encima de 2FC hará que un modulador tenga el mismo espectro de salida que un multiplicador. En frecuencias de señal por encima de Nyquist, las cosas se vuelven más complejas.
La Figura 5 muestra lo que sucede cuando la banda de la señal está justo debajo FC. Todavía es posible separar los productos armónicos de los producidos por la fundamental, pero ahora requiere un LPF con una caída muy pronunciada.
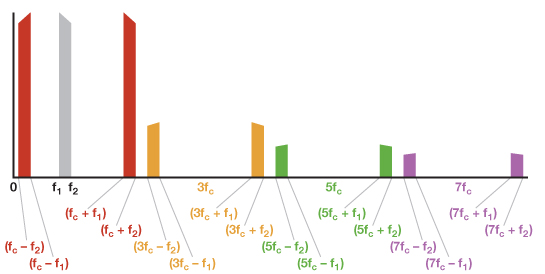
La Figura 6 muestra que a medida que la banda de la señal pasa a través FClos productos armónicos ahora se superponen (3FC – F1) < (FC + F1), por lo que los productos fundamentales ya no pueden separarse de los productos armónicos por un LPF. Las señales requeridas ahora deben ser seleccionadas por un filtro de paso de banda (BPF).
Por lo tanto, aunque los moduladores son mejores que los multiplicadores lineales para la mayoría de las aplicaciones de cambio de frecuencia, es importante considerar sus productos armónicos al diseñar sistemas reales.
Referencias
Diálogo analógico
Brandón, David. "El DDS multicanal permite la modulación FSK coherente en fase". Diálogo analógicoVolumen 44, Número 4, 2010.
Gilbert, Barrie. "Considerando multiplicadores (Parte 1)". Diálogo analógicoVolumen 42, Número 4, 2008.
Páginas de productos
Mezcladores/Multiplicadores
Multiplicadores/Divisores
Moduladores/Demoduladores
RAQ
Multiplicadores y Moduladores
Emptor de advertencia
Tutoriales
MT-079: Multiplicadores Analógicos
MT-080: Mezcladores y Moduladores
Si quieres conocer otros artículos parecidos a Multiplicadores vs Moduladores | Dispositivos analógicos puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!