el teorema de Thévenin | Circuito equivalente de Thévenin

Definición del teorema de Thévenin

Definición

Cualquier red de dos terminales que contenga resistencias y fuentes de voltaje y/o fuentes de corriente puede reemplazarse por un bebedero de un solo voltaje en serie con una sola resistencia. La fem de la fuente de voltaje es la fem de circuito abierto a través de los terminales de la red, y la resistencia en serie es la resistencia a través de los terminales de la red cuando las fuentes se establecen en cero.

Supongamos que se nos da un circuito arbitrario que contiene algunos o todos los siguientes: resistores, fuentes de voltaje, fuentes de corriente (la fuente puede ser tanto dependiente como independiente). Identifiquemos un par de nodos, digamos los nodos a y b, para que el circuito se pueda dividir en dos partes como se muestra en la Figura 1.

Fig.1: Circuito dividido en dos partes

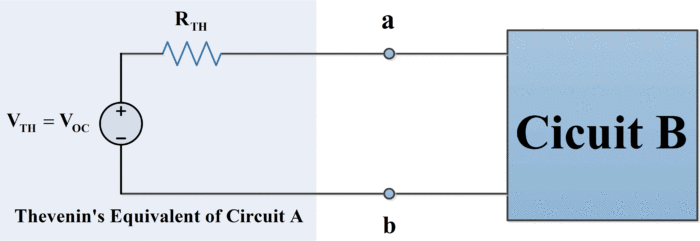
Además, es probable que ninguna fuente dependiente en el circuito A dependa de una variable en el circuito B y viceversa. Entonces podemos modelar el circuito A mediante una fuente de voltaje independiente adecuada, llamémosla V_{de oc} está conectado en serie con una resistencia adecuada, ponle R_mi. Esta combinación en serie de fuente de tensión y resistencia se denomina equivalente de Thevenin del circuito A. En otras palabras, el circuito A en la Figura 1 tiene el mismo efecto que el circuito en el cuadro sombreado en la Figura 2 en el circuito B. Este resultado se conoce como el teorema de Thévenin y es uno de los conceptos más útiles y significativos en la teoría de circuitos.

Fig.2: Circuito equivalente de Thevenin

Ruta B (a menudo denominada carga) puede constar de múltiples elementos de circuito, un solo elemento (resistencia de carga) o ningún elemento.

• También puedes leer: Teorema de Norton con soluciones de ejemplo

Tensión de circuito abierto equivalente de Thevenin

Para encontrar el voltaje V_{de oc}- llamado voltaje de circuito abierto - retire el circuito B del circuito A y determine el voltaje entre el nodo ayb (donde el + está en el nodo a). Este voltaje es V, como se muestra en la Figura 3(a)._{de oc}.

Fig.3(a): Determinación del voltaje de circuito abierto

Resistencia equivalente de Thévenin

Hay varias formas de encontrar la resistencia de Thevenin equivalente, que se detallan a continuación:
1. Para encontrar la resistencia R_mi– llamada resistencia equivalente de Thévenin para el circuito A:
yo) Retire el circuito B del circuito A.
ii) Establezca todas las fuentes independientes del circuito A en cero. (Una fuente de voltaje cero es equivalente a un cortocircuito y una fuente de corriente cero es equivalente a un circuito abierto).
iii) Encuentre la resistencia entre los nodos a y b - esto es R_mi– como se muestra en la Figura 3(b).

Fig.3(b): Determinación de la resistencia de Thevenin equivalente R_mi

2. La corriente de cortocircuito I es entonces detectada por los terminales de cortocircuito a y b_{Carolina del Sur}. La resistencia equivalente de Thevenin está dada por

[{{text{R}}_{text{th}}}text{= }{{text{V}}_{text{oc}}}text{/}{{text{I}}_{text{sc}}}text{= }{{text{V}}_{text{th}}}text{/}{{text{I}}_{text{sc}}}]

3. Cuando la red fuente tiene una estructura de escalera y no tiene fuentes controladas (dependientes), R_mi Se obtiene fácilmente por reducción serie-paralelo de la red muerta.

Cuando la red de origen fuentes controladasLa resistencia de Thevenin se puede encontrar utilizando el método que se muestra en la Figura 4.

Fig.4: determinación de la resistencia Thévenin

Aquí la red de fuente muerta está conectada a una fuente de prueba externa. Esta fuente de prueba puede ser cualquier voltaje o fuente de corriente independiente que establezca v_de en las terminales. Dado que la red muerta consta solo de resistencias y fuentes de control, y dado que R_mi igual a la resistencia equivalente de la red muerta, el teorema de la resistencia equivalente nos dice que

[{{R}_{TH}}={{v}_{o}}/{{i}_{o}}]

Un ejemplo de resolución del teorema de Thevenin con una fuente de voltaje

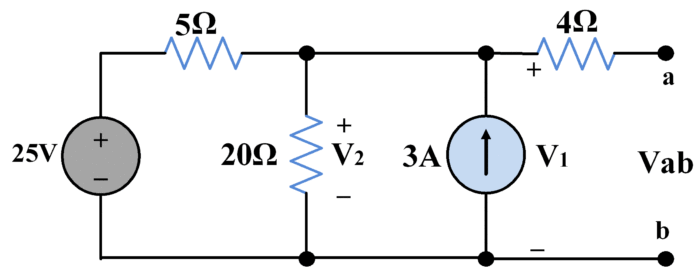
Encuentre el circuito equivalente de Thevenin de la siguiente red.

Aplicando el método de tensión nodal,

$frac{{{V}_{1}}-25}{5}+frac{{{V}_{1}}}{20}-3=0$

${{V}_{1}}=32~V$

${{V}_{th}}=32V$

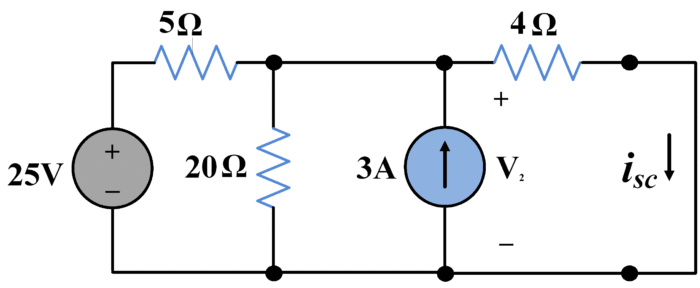
Para encontrar la corriente de cortocircuito, cortocircuitamos las terminales a y b como se muestra en la siguiente figura:

Nuevamente usando el método de voltaje nodal,

$frac{{{V}_{2}}-25}{5}+frac{{V}_{2}}}{20}-3+frac{{{V}_{2} } {4}=0$

${{V}_{2}}=16~V$

${{I}_{sc}}=frac{{{V}_{2}}}{4}=frac{16}{4}=4A$

Asi que,

${{R}_{th}}=frac{{{V}_{th}}}{{{I}_{sc}}}=frac{32}{4}$

${{R}_{th}}=8~Omega$

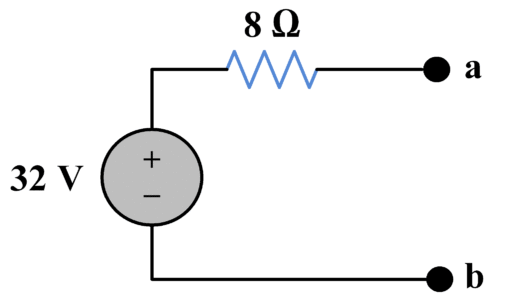
Ahora, Tenemos el siguiente circuito equivalente:

El teorema de Thevenin resolvió el problema con fuentes dependientes

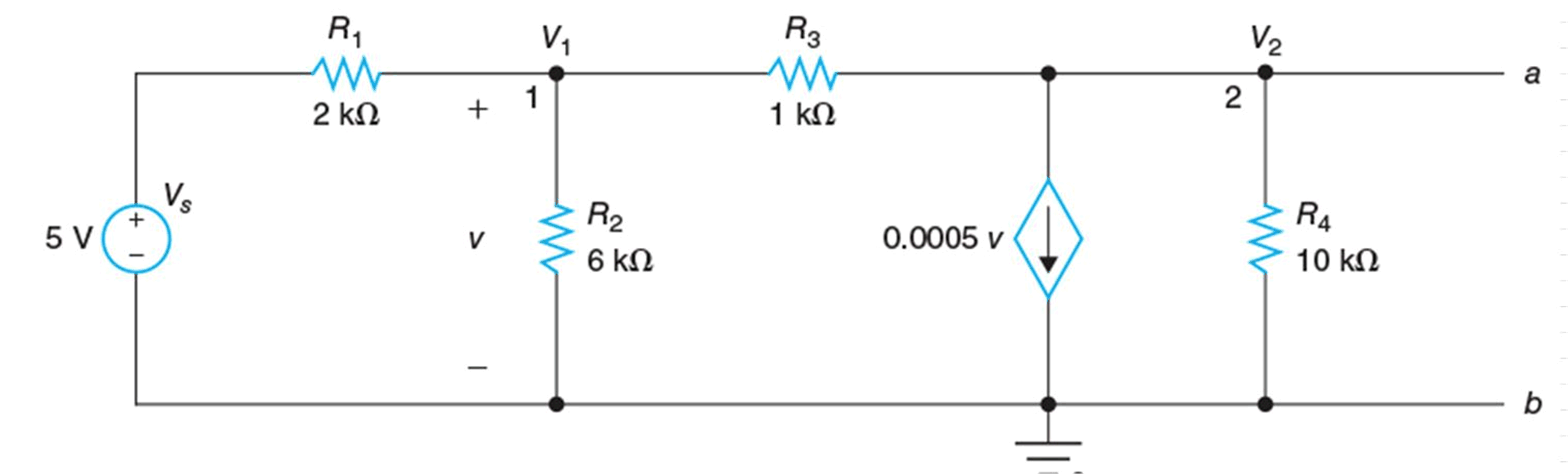
Considere un circuito que se muestra en la siguiente figura. Determinaremos V_mi y R_mi entre las terminales a y b del circuito.

Aplicación de KCL al Nodo 1:

[begin{matrix}   frac{{{V}_{1}}-5}{2000}+frac{{{V}_{1}}}{6000}+frac{{{V}_{1}}-{{V}_{2}}}{1000}=0 & cdots  & (1)  end{matrix}]

Multiplicando (1) por 6000 da

[3{{V}_{1}}text{- }15text{ }+text{ }{{V}_{1}}+text{ }6{{V}_{1}}text{ -}6{{V}_{2}}=text{ }0]

[10{{V}_{1}}=text{ }6{{V}_{2}}+text{ }15]

[{{V}_{1}}=text{ }0.6{{V}_{2}}+text{ }1.5]

Aplicación de KCL al nodo 2:

[begin{matrix}   frac{{{V}_{2}}-{{V}_{1}}}{1000}+0.0005{{V}_{1}}+frac{{{V}_{2}}}{10000}=0 & cdots  & (2)  end{matrix}]

Multiplicando (2) por 10000 da

[10{{V}_{2}}text{ -}10{{V}_{1}}+text{ }5{{V}_{1}}+text{ }{{V}_{2}}=text{ }0]

[11{{V}_{2}}text{ -}5{{V}_{1}}=text{ }0]

[11{{V}_{2}}text{- }5(0.6{{V}_{2}}+text{ }1.5)text{ }=text{ }0]

[8{{V}_{2}}=text{ }7.5]

Finalmente tenemos

[{{V}_{th}}=text{ }{{V}_{oc}}=text{ }{{V}_{2}}=text{ }7.5/8text{ }=text{ }0.9375text{ }V]

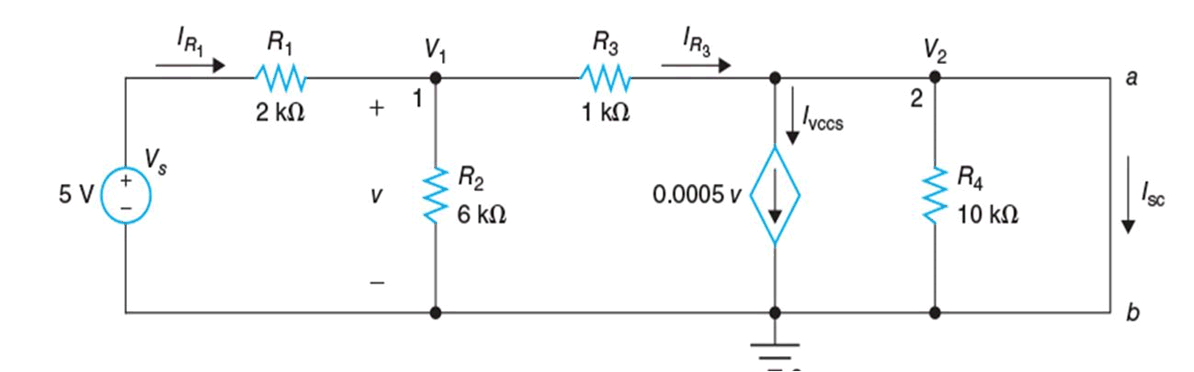
Ahora tenemos una fuente dependiente, por lo que el método 1 no se puede usar para encontrar la resistencia equivalente Rth. Aquí se puede utilizar el método 2 o el método 3. Nosotros preferimos usar el segundo método. Los terminales a y b deben cortocircuitarse como se muestra en la siguiente figura y V₂ = 0.

Aplicación de KCL al Nodo 1:

[begin{matrix}   frac{{{V}_{1}}-5}{2000}+frac{{{V}_{1}}}{6000}+frac{{{V}_{1}}}{1000}=0 & cdots  & (3)  end{matrix}]

Multiplicando (3) por 6000:

[3{{V}_{1}}text{- }15text{ }+text{ }{{V}_{1}}+text{ }6{{V}_{1}}=text{ }0]

[10{{V}_{1}}=text{ }15]

[{{V}_{1}}=text{ }1.5text{ }Vto text{ }vtext{ }=text{ }{{V}_{1}}=text{ }1.5text{ }V]

La corriente a través de R₃ (⟶) está dado por

[{{I}_{{{R}_{3}}}}=text{ }{{V}_{1}}/{{R}_{3}}=~1.5text{ }V/1kOmega =text{ }1.5mA]

La corriente a través de VCCS (↓) viene dada por

[{{I}_{VCCS}}=text{ }0.0005{{V}_{1}}=~0.0005*1.5text{ }Atext{ }=text{ }0.75mA]

Ahora la corriente haría un cortocircuito

[{{I}_{sc}}=text{ }{{I}_{{{R}_{3}}}}text{ -}{{I}_{VCCS}}=text{ }1.5mAtext{ -}0.75mA=text{ }0.75mA]

Y la resistencia equivalente es Thévenin

[{{R}_{th}}={{V}_{th}}/{{I}_{sc}}=text{ }0.9675text{ }V/0.75mA=text{ }1.25text{ }kOmega ]

Resumen del teorema de Thevenin

Los siguientes pasos se utilizan para determinar el circuito equivalente de Thevenin.

1. Se retira la parte del circuito que se considera carga.
2. El voltaje de circuito abierto V_{de oc} se calcula en los terminales.
3. Para calcular R_mi

• Cortocircuite cada fuente de tensión independiente.
• Circuito abierto todas las fuentes de corriente independientes.

4. Dibuje un circuito equivalente, conecte la carga y determine la corriente de carga.