Control de retroalimentación de bajo ruido con giroscopios MEMS
Resumen
Los giroscopios MEMS proporcionan un medio sencillo de medir la velocidad angular de rotación en paquetes que se acoplan fácilmente a las placas de circuito impreso, por lo que son una opción popular para servir como elemento sensor de retroalimentación en muchos tipos diferentes de sistemas de control de movimiento. En este tipo de funciones, el ruido de las señales de velocidad angular (salida del giroscopio MEMS) puede influir directamente en los comportamientos críticos del sistema, como la estabilidad de la plataforma, y suele ser el factor determinante del nivel de precisión que puede soportar un sistema de control. Por lo tanto, el bajo nivel de ruido es un valor natural para guiar a los arquitectos y desarrolladores de sistemas a la hora de definir y desarrollar nuevos sistemas de control de movimiento. Llevando este valor (bajo ruido) un paso más allá, traducir los criterios críticos a nivel de sistema, como la precisión de apuntamiento, en mediciones de ruido que suelen estar disponibles en las hojas de datos de los giroscopios MEMS, es una parte muy importante del trabajo inicial de diseño y arquitectura. Entender la dependencia del sistema del comportamiento del ruido del giroscopio tiene una serie de ventajas, como la posibilidad de establecer los requisitos pertinentes para el elemento sensor de retroalimentación o, por el contrario, analizar la respuesta del sistema al ruido de un giroscopio concreto. Una vez que los diseñadores de sistemas comprendan bien esta relación, podrán centrarse en controlar las dos áreas clave de influencia que tienen sobre los comportamientos del ruido en sus bucles de retroalimentación de la velocidad angular: 1. desarrollar los criterios más adecuados para la selección del giroscopio MEMS y 2. preservar el rendimiento del ruido disponible a lo largo del proceso de integración del sensor.
Principios básicos del control del movimiento
El desarrollo de una relación útil entre los comportamientos del ruido en un giroscopio MEMS y su impacto en los comportamientos clave del sistema suele comenzar con una comprensión básica de cómo funciona el sistema. La figura 1 ofrece un ejemplo de arquitectura para un sistema de control de movimiento, que desglosa los elementos clave del sistema en bloques funcionales. El objetivo funcional de este tipo de sistemas es crear una plataforma estable para el personal o los equipos que pueden ser sensibles al movimiento inercial. Un ejemplo de aplicación es una antena de microondas en una plataforma de vehículo autónomo que maniobra en condiciones difíciles a una velocidad que provoca cambios bruscos en la orientación del vehículo. Sin un control en tiempo real del ángulo de apuntamiento, estas antenas altamente direccionales pueden no ser capaces de soportar una comunicación continua mientras se someten a este tipo de movimiento inercial.
El sistema de la figura 1 utiliza un servomotor, que idealmente girará de forma igual y opuesta a la rotación que sufrirá el resto del sistema. El bucle de retroalimentación comienza con un giroscopio MEMS que observa la velocidad de rotación (ωG) en la plataforma estabilizada. Las señales de velocidad angular del giroscopio se introducen en un procesamiento digital de señales específico para la aplicación, que incluye el filtrado, la calibración, la alineación y la integración para producir una respuesta de orientación en tiempo real (φE). La señal de control de los actuadores (φCOR) proviene de la comparación de esta señal de retroalimentación con la orientación ordenada (φCMD), que pueden proceder de un sistema central de control de la misión o simplemente representar la orientación que soporta el funcionamiento ideal del equipo en la plataforma.
Ejemplo de aplicación
Partiendo de la visión arquitectónica de un sistema de control de movimiento de la Figura 1, también se obtienen valiosas definiciones y conocimientos del análisis de los atributos físicos específicos de la aplicación. Considera el sistema de la figura 2, que ofrece una vista conceptual de un sistema de inspección automatizado para una línea de producción. Este sistema de cámaras inspecciona los artículos que entran y salen de su campo de visión en una cinta transportadora. En esta disposición, la cámara se fija al techo mediante un soporte largo, que establece su altura (véase D en la figura 2), para optimizar su campo de visión en función del tamaño de los objetos que va a inspeccionar. Como las fábricas están llenas de maquinaria y otras actividades, la cámara puede experimentar movimientos oscilantes (ver ωSW


La técnica de control de movimiento más aplicable a este tipo de sistemas se conoce como estabilización de imagen. Los primeros sistemas de estabilización de imagen utilizaban sistemas de retroalimentación basados en giroscopios para accionar servomotores, que ajustaban la orientación del sensor de imagen durante el tiempo que el obturador estaba abierto. La aparición de la tecnología MEMS ha permitido reducir el tamaño, el coste y la potencia de estas funciones de forma revolucionaria, lo que ha hecho que se generalice el uso de esta técnica en las cámaras digitales modernas. Los avances en las técnicas de procesamiento digital de imágenes, que siguen utilizando en sus algoritmos las mediciones de velocidad angular basadas en MEMS, han permitido eliminar el servomotor en muchas aplicaciones. Tanto si la estabilización de la imagen procede de un servomotor como del postprocesamiento digital de los archivos de imagen, la función fundamental (detección de retroalimentación) del giroscopio sigue siendo la misma, al igual que la consecuencia de su ruido. Para simplificar, esta discusión se centra en el enfoque clásico (servomotor en el sensor de imagen) para explorar los fundamentos de ruido más relevantes, y cómo se relacionan con los atributos físicos más importantes de este tipo de aplicación.
Paseo angular aleatorio (ARW)
Todos los giroscopios MEMS tienen ruido en sus mediciones de velocidad angular. Este ruido inherente al sensor representa la variación aleatoria de la salida del giroscopio, cuando funciona en condiciones ambientales inerciales (sin movimiento de rotación) y estáticas (sin vibraciones ni golpes). Los parámetros más comunes que las hojas de datos de los giroscopios MEMS proponen para describir su comportamiento acústico son la densidad de ruido de la tasa (RND) y el recorrido aleatorio del ángulo (ARW). El parámetro RND suele utilizar unidades de °/seg/√Hz y proporciona una forma sencilla de predecir el ruido total, en términos de velocidad angular, basándose en la respuesta en frecuencia del giroscopio. El parámetro ARW suele utilizar unidades de °/√hora y suele ser más útil para analizar el impacto que tiene el ruido en la estimación del ángulo durante periodos de tiempo concretos. La ecuación 2 proporciona una fórmula genérica para estimar el ángulo, basada en la medición de la velocidad angular. Además, también proporciona una fórmula sencilla que relaciona el parámetro RND con el parámetro ARW. Esta relación representa una pequeña adaptación (FFT de una cara frente a la de dos caras) de la norma IEEE-STD-952-1997 (Apéndice C).

La figura 3 ofrece una referencia gráfica que ayuda a profundizar en el comportamiento que representa el parámetro ARW. Las líneas punteadas verdes de esta ilustración representan el comportamiento del ARW cuando el giroscopio tiene un RND de 0,004°/seg/√Hz, lo que equivale a un ARW de 0,17°/√hora. Las líneas continuas representan seis integraciones separadas de la salida de este giroscopio durante un periodo de 25 ms. La naturaleza aleatoria de los errores angulares, con respecto al tiempo, muestra que la principal utilidad del ARW es estimar la distribución estadística de los errores angulares a lo largo de un tiempo de integración específico. Ten en cuenta también que este tipo de respuesta implica el uso de un filtrado de paso alto para eliminar los errores de sesgo iniciales en el proceso de integración.

Volviendo al ejemplo de aplicación de la figura 2, la combinación de las ecuaciones 1 y 2 ofrece la oportunidad de relacionar criterios importantes (distorsión física en la superficie de inspección) con las métricas de rendimiento del ruido (RND, ARW) que suelen estar disponibles en las hojas de datos de los giroscopios MEMS. En este proceso, suponer que el tiempo de integración (τ) de la ecuación 1 es igual al tiempo de captura de la imagen proporciona otra simplificación que podría ser útil. La ecuación 3 aplica la relación genérica de la ecuación 1 para estimar que cuando la cámara está a 1 metro (D) de la superficie de inspección y el error de distorsión máximo permitido es de 10 µm (dRE), el error angular del giroscopio (φRE) debe ser inferior a 0,00057.°
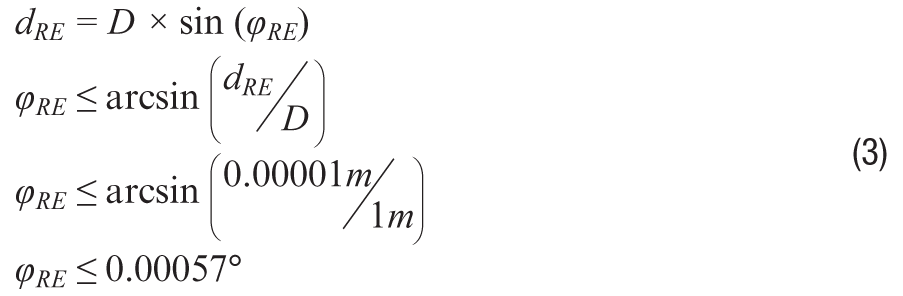
La ecuación 4 combina los resultados de la ecuación 3 y la relación genérica de la ecuación 2 para predecir los requisitos de ARW y RND del giroscopio MEMS en una situación concreta. Este proceso supone que los tiempos de captura de la imagen de 35 ms representan el tiempo de integración (τ) de la ecuación 2, lo que lleva a la predicción de que el ARW del giroscopio debe ser inferior a 0,18°/√hora, o el RND debe ser inferior a 0,0043°/seg/√Hz para cumplir este requisito. Por supuesto, éste puede no ser el único requisito que soportan estos parámetros, pero estas sencillas relaciones proporcionan un ejemplo de cómo relacionarse con requisitos y condiciones conocidos.

Ruido de la velocidad angular en función del ancho de banda
Aquellos que desarrollen sistemas que proporcionen un control de apuntamiento continuo pueden preferir evaluar el impacto del ruido en términos de velocidad angular, ya que pueden no tener un tiempo de integración fijo para explotar la relación basada en el RND. Evaluar el ruido en términos de velocidad angular suele implicar tener en cuenta el parámetro RND y la respuesta en frecuencia en la cadena de señales del giroscopio. La respuesta en frecuencia del giroscopio suele estar más influenciada por el filtrado, que admite los requisitos específicos de la aplicación para los criterios de estabilidad del bucle y el rechazo de la respuesta no deseada del sensor a las amenazas ambientales, como las vibraciones. La ecuación 5 proporciona una forma sencilla de estimar el ruido asociado a una determinada respuesta en frecuencia (ancho de banda de ruido) y RND.

Cuando la respuesta en frecuencia del RND sigue un perfil de filtro paso bajo de uno o dos polos, el ancho de banda del ruido (fNBW) se refiere a la frecuencia de corte del filtro (fC) según las relaciones de la ecuación 6.

Por ejemplo, la figura 4 ofrece dos gráficos espectrales diferentes para el ruido del ADXRS290, que tiene un NDR de 0,004°/seg/√Hz. En este gráfico, la curva negra representa la respuesta al ruido cuando se utiliza un filtro de paso bajo bipolar, cuya frecuencia de corte es un filtro de 200 Hz, mientras que la curva azul representa la respuesta al ruido cuando se utiliza un filtro de paso bajo unipolar, cuya frecuencia de corte es un filtro de 20 Hz. La ecuación 7 proporciona los cálculos del ruido total de cada uno de estos filtros. Como era de esperar, el ruido de la versión de 200 Hz es mayor que el de la versión de 20 Hz.


En los casos en que el sistema requiere un filtrado personalizado, cuya respuesta en frecuencia (HDF(f)) no se ajusta a los modelos simples de uno y dos polos de las ecuaciones 6 y 7, la ecuación 8 proporciona una relación más genérica para predecir el ruido total:

Además de influir en el ruido total de la velocidad angular, los filtros giroscópicos también contribuyen al retardo de fase de la respuesta global del bucle, que tiene un impacto directo en otro importante factor de mérito en los sistemas de control de retroalimentación: el margen de fase en la frecuencia de cruce de la ganancia unitaria. La ecuación 9 proporciona una fórmula para estimar el retardo de fase (θ) que un filtro unipolar (fC = frecuencia de corte) tendrá sobre la respuesta en frecuencia de los lazos de control, en su frecuencia de cruce de ganancia unitaria (fG). Los dos ejemplos de la ecuación 9 ilustran el retardo de fase a una frecuencia de cruce de ganancia unitaria de 20 Hz, para filtros con frecuencias de corte de 200 Hz y 60 Hz, respectivamente. Este impacto en el margen de fase puede llevar a especificar anchos de banda del giroscopio 10 veces mayores que la frecuencia de cruce de ganancia unitaria, lo que puede poner aún más énfasis en la selección de un giroscopio MEMS con niveles de RND favorables.

Los sistemas de control modernos suelen utilizar filtros digitales, que pueden tener diferentes modelos para predecir su retardo de fase en las frecuencias críticas para el bucle de control. Por ejemplo, la ecuación 10 presenta una fórmula para predecir el retardo de fase (θ) asociado a un filtro FIR de 16 tomas (NTAP), que funciona con el SPS 4250 (fS) del ADXRS290, con la misma frecuencia de cruce de ganancia unitaria (fG) de 20 Hz. Este tipo de relación puede ayudar a determinar el número total de tomas que una arquitectura de sistema puede permitir para este tipo de estructura de filtro.
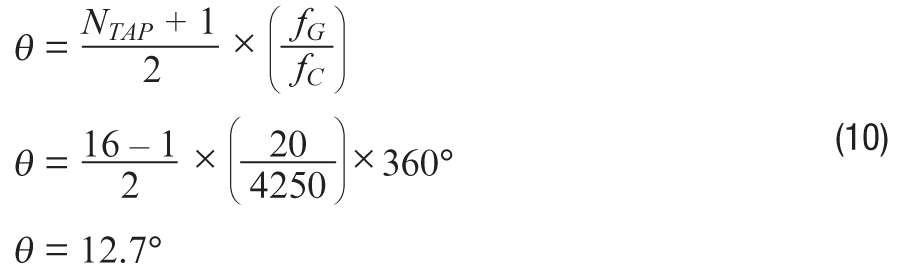
Conclusión
La conclusión es que el ruido en los bucles de retroalimentación de la velocidad angular puede tener una influencia directa en los criterios clave de rendimiento de los sistemas de control de movimiento, por lo que debe tenerse en cuenta lo antes posible en el proceso de diseño de un nuevo sistema. Los que puedan cuantificar cómo influirá el ruido de la velocidad angular en los comportamientos del sistema tendrán una ventaja considerable sobre los que sólo saben que necesitan poco ruido. Podrán establecer objetivos de rendimiento que creen un valor observable en sus aplicaciones, y estarán en una posición excelente para cuantificar las consecuencias a nivel de sistema cuando otros objetivos del proyecto animen a considerar un giroscopio MEMS específico. Una vez que se han adquirido estos conocimientos básicos, los diseñadores de sistemas pueden centrarse en identificar un giroscopio MEMS que cumpla sus requisitos de rendimiento, utilizando las métricas de ancho de banda, densidad de ruido de la tasa o recorrido aleatorio del ángulo para guiar su pensamiento. Cuando buscan optimizar el rendimiento del ruido que obtienen de los sensores que seleccionan, pueden utilizar las relaciones con el ancho de banda (ruido de velocidad angular) y el tiempo de integración (error angular) para impulsar otras definiciones importantes a nivel de sistema que apoyarán el rendimiento más adecuado para la aplicación.
Si quieres conocer otros artículos parecidos a Control de retroalimentación de bajo ruido con giroscopios MEMS puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!