Amplificadores de retroalimentación de corriente de compensación en aplicaciones de fotocorriente
Introducción
Históricamente, los amplificadores de retroalimentación de corriente (CFA) no han sido la primera opción para su uso como amplificadores de transimpedancia (TIA) debido a sus corrientes de entrada inversoras relativamente altas y al ruido de la corriente de entrada inversora, que puede ser al menos un orden de magnitud mayor que el de un amplificador de retroalimentación de tensión (VFA) comparable. Además, muchos diseñadores de sistemas no están familiarizados con las AFV y, por tanto, se sienten menos cómodos utilizándolas. Sin embargo, los AFC son bastante fáciles de usar y pueden superar a sus homólogos VFA en aplicaciones que requieren alta ganancia, baja potencia, bajo ruido, amplio ancho de banda y alta velocidad de giro. Una de sus principales ventajas es que la ganancia de bucle de un ideal El CFA es independiente de su ganancia en bucle cerrado, lo que le permite ofrecer un excelente rendimiento de distorsión armónica y ancho de banda, independientemente de su ganancia en bucle cerrado.
Debido a su bajísima corriente de polarización de entrada y al ruido de la corriente de entrada, los amplificadores operacionales de entrada FET suelen ser los más considerados para las aplicaciones TIA, especialmente los que utilizan dispositivos de baja corriente de salida, como los elementos fotoeléctricos, como fuente de corriente de entrada. Aunque los amplificadores de entrada FET destacan en muchas de estas aplicaciones, su velocidad puede ser insuficiente en sistemas que requieren un rendimiento más rápido. Así, los CFA se utilizan cada vez más como TIA en sistemas más rápidos que pueden tolerar más ruido.
Este artículo analiza cómo la capacitancia parásita de un fotodiodo u otro transductor de luz a corriente afecta a un CFA que funciona como TIA, y cómo compensar adecuadamente el amplificador por esta capacitancia. Se proporciona algún material introductorio sobre el funcionamiento de los AFC, así como paralelos ocasionales entre los análisis de los AFC y los AFV. No se utiliza el análisis de la "ganancia de ruido" de los circuitos VFA ni la "impedancia de retroalimentación" de los circuitos CFA. En su lugar, se utiliza la teoría clásica de la retroalimentación mediante la ganancia de bucle para evitar las dificultades que surgen al pasar del dominio de la corriente al de la tensión (la ganancia de bucle es siempre una cantidad adimensional) y porque la propia teoría presenta diagramas de Bode que son sencillos y fáciles de utilizar.
Principios básicos de los amplificadores de retroalimentación de corriente
Un CFA ideal tiene una impedancia de entrada nula, un cortocircuito entre sus entradas, porque la señal de retroalimentación negativa es una corriente. En cambio, un VFA ideal tiene una impedancia de entrada infinita porque su señal de retroalimentación es una tensión. El CFA detecta la corriente de error que circula por su entrada y desarrolla una tensión de salida igual a Z veces la corriente de entrada, donde Z representa la ganancia de transimpedancia. La dirección de la corriente de error se ajusta para producir una retroalimentación negativa. Al igual que A en un VFA, Z se aproxima al infinito en un CFA ideal. La figura 1 muestra los fundamentos de la configuración de un CFA ideal como TIA para transferir la corriente de una fuente de corriente ideal a su tensión de salida.
La ganancia en bucle cerrado de este IAT puede expresarse como sigue
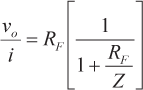 |
(1) |
La ecuación 1 muestra que a medida que Z se acerca al infinito, la ganancia de la TIA se aproxima a su valor ideal de RF. A medida que Z se acerca al infinito, la corriente de error, iese aproxima a cero, y toda la corriente de entrada fluye a través de RF. La ganancia del bucle se ve como
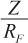
en la ecuación 1.
Desgraciadamente, los CFA ideales no existen, por lo que los dispositivos prácticos utilizan lo más parecido: un búfer de ganancia unitaria en sus entradas. Un espejo de corriente refleja la corriente de error a un nodo de alta impedancia donde se convierte en tensión, se amortigua y se envía a la salida, como se muestra en la figura 2.
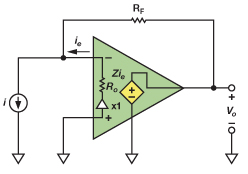
Mientras Ro = 0, la ganancia del bucle cerrado es la misma que la dada en la ecuación 1. Cuando Ro > 0, la ganancia del bucle cerrado se convierte en
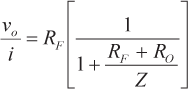 |
(2) |
y la ganancia del bucle es

Diseño de TIA con componentes prácticos
Los fotodiodos y otros dispositivos fotoeléctricos tienen una capacidad parásita en derivación proporcional al área del dispositivo. Cuando Ro = 0, esta capacitancia está totalmente cebada, por lo que no tiene ningún efecto en la respuesta del bucle cerrado. En un verdadero AFC, Ro > 0, y la capacitancia parásita influye en la respuesta, lo que puede hacer que el circuito sea inestable. Además, al igual que la ganancia en bucle abierto, A, en un VFA, la magnitud de Z en un CFA verdadero es grande a baja frecuencia y disminuye al aumentar la frecuencia, y el desplazamiento de fase es más lento al aumentar la frecuencia. En primer orden, Z(s) puede caracterizarse por un único polo dominante en s = p y una transimpedancia en corriente continua de Zocomo se indica en la ecuación 3. Los polos de alta frecuencia de Z(s) se discutirán más adelante.
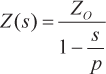 |
(3) |
El circuito de la figura 3 incluye la capacitancia parásita, C, y la transimpedancia, Z(s). Ten en cuenta que la capacitancia de entrada inversora del AFC puede ser absorbida por C.

La ecuación 4 se obtiene realizando un KCL en la entrada inversora.
|
|
(4) |
La corriente de error, iees
|
|
(5) |
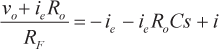
Combinando la ecuación 4 y la ecuación 5, se obtiene el siguiente resultado para la ganancia TIA en bucle cerrado del circuito de la figura 3:
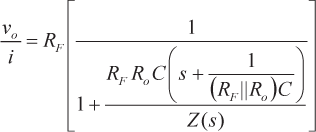 |
(6) |
La ganancia del bucle es evidente en la ecuación 6 y viene dada por
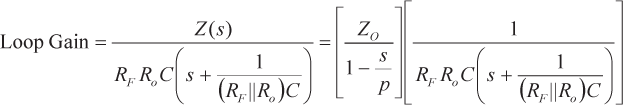 |
(7) |
La ganancia del bucle contiene dos polos, uno de baja frecuencia en s = p y un polo de alta frecuencia en

Cuando Ro<< RFla combinación paralela de RF y Ro puede aproximarse mediante Ro. Ambos polos tienen un problema de estabilidad cuando el polo de alta frecuencia se produce a una frecuencia en la que la magnitud de la ganancia del bucle es superior a 0 dB. Cuando Ro y C son pequeños, el polo espurio se produce a una frecuencia superior a la de cruce, y el amplificador es estable. Sin embargo, éste no suele ser el caso en la mayoría de los circuitos TIA, por lo que tenemos que encontrar una forma de compensar la capacitancia parásita de la entrada inversora.
Añadir un condensador de retroalimentación (una breve digresión)
Un CFA con una función de transferencia unipolar, como se muestra en la ecuación 3, es estable con cualquier valor de resistencia de realimentación porque el desplazamiento de fase de retardo alrededor de su bucle de realimentación está limitado a -90°. Sin embargo, los polos secundarios de los CFA reales introducen un gran desfase a altas frecuencias, lo que impone un límite práctico al valor mínimo de RF para garantizar la estabilidad (45° suele ser el margen de fase mínimo aceptable). A partir de este punto, Z(s) incluirá un polo de alta frecuencia en s = pHy el polo dominante s = p.
Para garantizar que la impedancia de realimentación no llegue a cero, la sabiduría popular dice que no debemos utilizar un condensador de realimentación en un circuito CFA. Pero no es tan sencillo, porque el condensador de realimentación introduce un desplazamiento de fase, además de los cambios de magnitud. Este apartado examina lo que ocurre cuando se añade un condensador de realimentación a un TIA basado en CFA, omitiendo por el momento la capacitancia parásita de entrada. La adición de un condensador de retroalimentación, CFa través de la resistencia de retorno, RFen el circuito de la figura 2 produce un polo y un cero en la ganancia del bucle. ZF se define como la combinación paralela de RF y CF:
 |
(8) |
Si RF en la ecuación 2 se sustituye por ZFentonces la ganancia del bucle cerrado se expresa mediante la ecuación 9.
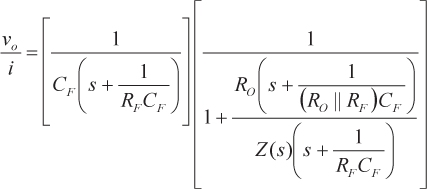 |
(9) |
La ganancia del bucle es entonces
 |
(10) |
La ganancia del bucle tiene un polo dominante en s = p y un polo de alta frecuencia en s = pH de Z(s). Además, tiene un polo en

y un cero en
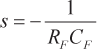
debido al condensador de retorno añadido.
En el diagrama de Bode, el cero debido a CF se produce a una frecuencia inferior a la del polo debido a CF porque la expresión de la frecuencia cero contiene RF en el denominador, y la expresión de la frecuencia del polo contiene (Ro||RF) en el denominador. El diagrama de Bode para una posible IAT basada en CFA con CF (Ecuación 10) se muestra en la Figura 4.
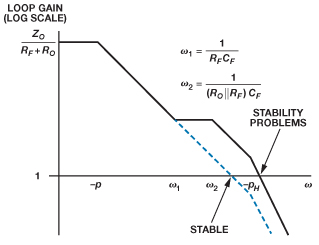
El cero produce una magnitud creciente y un desplazamiento de fase principal con el aumento de la frecuencia, lo que en algunas situaciones puede ser bueno desde el punto de vista de la estabilidad. Sin embargo, en el sistema modelado en la figura 4, el cero hace retroceder el punto en el que la ganancia del bucle pasa por 0 dB, y el polo en pHhace que la asíntota de magnitud caiga a -40 dB/década más allá del cruce. La línea azul punteada muestra la ganancia del bucle sin CFutilizando la ecuación 2 y la versión bipolar de Z(s), expresada en la ecuación 11.
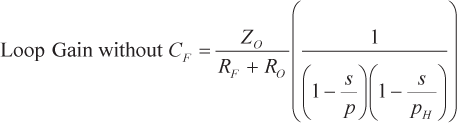 |
(11) |
La figura 4 muestra que el amplificador es estable sin CF pero desarrolla problemas de estabilidad cuando CF se añade. El gráfico de la Figura 4 no descarta por completo el uso de un condensador de realimentación, ya que esta Z(s) en concreto no es representativa de todos los CFA y no se utilizan los valores reales de las resistencias y los condensadores, pero muestra que el polo de alta frecuencia limita la cantidad de capacitancia de realimentación que puede aplicarse con seguridad. La figura 4 también muestra que se puede añadir con seguridad cualquier cantidad de capacitancia de retroalimentación a un hipotético CFA con una función de transferencia unipolar, y que añadir la capacitancia de retroalimentación ampliaría su ancho de banda en bucle cerrado.
Utilizando el cero debido al CFA para anular el polo debido a la capacitancia parásita
Ahora que el efecto de añadir CF a un CFA se entiende en un sentido general, se puede demostrar que CF puede utilizarse de forma segura para compensar la capacitancia parásita en derivación de una fuente de corriente de entrada.
La ganancia en bucle cerrado del circuito de la figura 3 se muestra en la ecuación 6. Para ver qué ocurre con este circuito cuando se añade un condensador de realimentación, RF puede sustituirse por ZF en la ecuación 6, de forma similar a lo que se hizo para desarrollar la ecuación 9, donde ZF se define en la ecuación 8. El circuito se muestra en la Figura 5.

La ganancia en bucle cerrado del circuito de la figura 5 viene dada por la ecuación 12
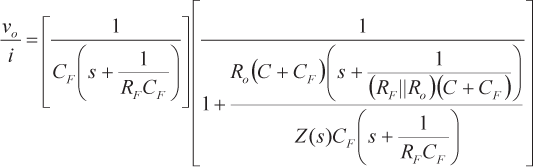 |
(12) |
a partir de la cual se puede determinar que la ganancia del bucle es

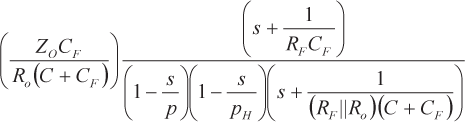 |
(13) |
El cero debido a CF en la ecuación 13 es el mismo que el cero de la ecuación 10, pero el polo debido a CF se trasladó de

para
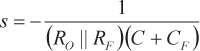
La adición de C a CF permite desplazar la posición del polo para que coincida con la posición cero, anulando así el polo debido a la capacitancia parásita, C, de la fuente de corriente de entrada. Fijando la frecuencia del polo debida a CF y C igual a la frecuencia cero debida a CF en la ecuación 13 da la ecuación 14 :
 |
(14) |
La ecuación 14 muestra la fórmula sencilla para calcular el valor de CFque anula el polo de la ganancia del bucle debido a la capacitancia parásita, C, en la TIA mostrada en la figura 5. Con esta cancelación perfecta de polos y ceros, la ganancia del bucle vuelve a su forma original con polos dominantes y de alta frecuencia, como en la ecuación 11. La ganancia del bucle cerrado puede expresarse ahora como se muestra en la ecuación 15.
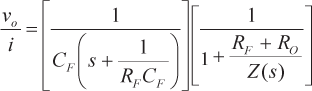 |
(15) |
La principal dificultad que se encuentra al utilizar la ecuación 14 es determinar Roque puede ser variable y no siempre se especifica en las hojas de datos del CFA. Sin embargo, no es necesario que la cancelación de polos y ceros sea exacta, siempre que la pendiente del gráfico de ganancia del bucle sea razonablemente cercana a -20 dB/década al pasar por 0 dB. La ecuación 14 muestra que CF disminuye linealmente con Ro debido al aumento de la carga de trabajo que se produce cuando Ro se aproxima a 0, donde C se convierte en un bootstrap completo y el CF es igual a 0. La ecuación 14 también puede expresarse como una constante de tiempo ajustada como RoC = RFCF. La forma adaptada de la constante de tiempo de la ecuación 14 es muy similar al resultado obtenido al compensar la VFA por la capacitancia parásita del nodo sumador: RGCG = RFCFdonde RG es la resistencia de ganancia de la VFA y CG es la capacidad a través de RGque suele ser la capacidad parásita del nodo sumador. Sin embargo, hay que pagar un precio por esta ventaja. Aunque la adición de CF estabiliza la TIA, también introduce un polo en la ganancia del bucle cerrado en

como se puede ver en la ecuación 12 y en la ecuación 15. La ganancia en bucle cerrado descrita por la ecuación 15 puede verse como dos sistemas en cascada con funciones de transferencia multiplicadas. El primer sistema tiene como función de transferencia el factor más a la izquierda de la ecuación 15 y tiene unas dimensiones de ohmios. La segunda tiene como función de transferencia el factor más a la derecha de la ecuación 15 y es adimensional.
La respuesta del segundo sistema se rige por la ganancia del bucle y se puede modelar mediante una función de transferencia de primer orden, siempre que la magnitud de la ganancia del bucle pase de 0 dB a -20 dB/década. La teoría básica de la retroalimentación muestra que si se cumple esta condición de amortiguación, la magnitud de la ganancia en bucle cerrado del segundo sistema es aproximadamente la unidad cuando la magnitud de la ganancia del bucle es >>1, y sigue la magnitud de la ganancia del bucle cuando la magnitud de la ganancia del bucle es <<1. El punto de 3 dB en la ganancia de bucle cerrado se produce en la frecuencia en la que la amplitud de la ganancia de bucle cruza 0 dB (si la pendiente es un poco más rápida que -20 dB/década, se producirá algún pico en la respuesta de bucle cerrado cerca del punto de cruce de 0 dB). Por lo tanto, en un amplificador estable, el segundo sistema puede aproximarse como un filtro de paso bajo de primer orden con ganancia unitaria en la banda pasante y una frecuencia de corte igual a la frecuencia en la que la magnitud de la ganancia del bucle cruza 0 dB. La función de transferencia del primer sistema es la recíproca del factor de realimentación y tiene una respuesta simple de paso bajo de primer orden con un valor de RF en cc y una frecuencia de esquina de

Intuitivamente, el polo adicional debido a CF es lógico porque la tensión de salida se desarrolla por la corriente que fluye en la impedancia de retroalimentación, que disminuye al aumentar la frecuencia. El polo se forma donde la reactancia de CF es igual al valor de RF. Esta misma situación se da en los TIA basados en VFA que utilizan compensación de condensadores de retroalimentación. Sin embargo, el ancho de banda del bucle cerrado puede aumentarse un poco disminuyendo cuidadosamente CF del valor calculado en la ecuación 14, desplazando la frecuencia de los polos y reduciendo el margen de fase, pero esto debe hacerse experimentalmente.
Datos de la simulación
Para comprobar este resultado, se desarrolló un modelo de simulación simple para un AFC con Zo = 1 MΩ, p = -2π (100 kHz), pH = -2π (200 MHz), Ro = 50 Ω, y RF = 500 Ω. La magnitud de la ganancia del bucle se encuentra tomando la magnitud de la ecuación 11 con estos valores.
 |
(16) |
que es igual a 1 en torno a f = 145 MHz.
El desplazamiento de fase de la ganancia del bucle a 145 MHz viene dado por
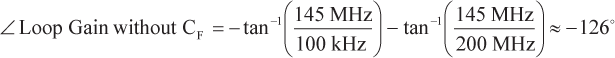 |
(17) |
lo que da un margen de fase de unos 54°, que es un punto de partida razonable para un CFA básico sin capacitancias parásitas.
La figura 6 muestra la simulación de la respuesta de este modelo a una entrada de paso de corriente con un tiempo de subida de 1 ns.
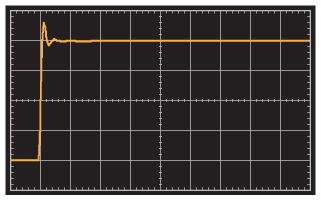
La respuesta es limpia, con un mínimo de timbre, exactamente lo que cabría esperar de un margen de fase de 54°. La respuesta al paso del mismo amplificador con un condensador parásito de 50 pF añadido entre la entrada inversora y tierra se muestra en la Figura 7.

La escala vertical de la Figura 7 es la misma que la de la Figura 6, pero el gráfico se ha desplazado una división hacia abajo para tener en cuenta el anillo. El anillo excesivo es evidente, y este amplificador tiene claramente un problema de margen de fase.
El amplificador se puede estabilizar añadiendo un condensador de realimentación determinado por la ecuación 14, que se calcula en 5 pF. La figura 8 muestra los resultados cuando se añade el condensador de realimentación de 5 pF.
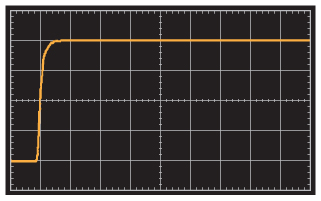
La limitación de banda debida al polo en la ganancia de bucle cerrado es evidente. Se determinó que el cruce de 0 dB en la ganancia de bucle del amplificador original era de 145 MHz, lo que corresponde a una constante de tiempo de aproximadamente 1,1 ns en un sistema de primer orden, y el RFCF la constante de tiempo es de 2,5 ns (ten en cuenta que la tasa de amortiguación de la amplitud de la ganancia del bucle es un poco más rápida que -20 dB/década en el cruce de 0 dB, ya que el margen de fase es inferior a 90°, pero el modelo de bucle cerrado de primer orden es una aproximación razonablemente precisa). Utilizando el modelo de dos sistemas en cascada como se ha descrito anteriormente, la constante de tiempo global de los sistemas en cascada puede estimarse como la raíz cuadrada de las dos constantes de tiempo (el tiempo de subida de la fuente de corriente de entrada del 10% al 90% de 1 ns corresponde a una constante de tiempo efectiva de menos de ns que es lo suficientemente corta como para ser ignorada), es decir, unos 2,7 ns, lo que parece ser correcto para la respuesta mostrada en la figura 7.
Al reducir el CF a 3 pF reduce un poco el margen de fase y aumenta la frecuencia de los polos del bucle cerrado, lo que acelera las cosas como se muestra en la figura 9.
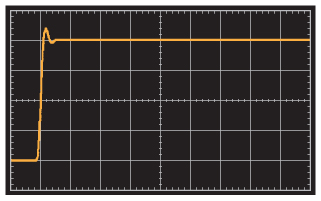
Está claro que puede ser necesario experimentar para obtener el mejor valor de CF. Otros factores como la capacidad de carga, la disposición de las tarjetas y las variaciones de Ro también son relevantes para la selección de CF.
Conclusión
Con el creciente interés por utilizar los CFA como TIA, es importante entender cómo se compensa la capacitancia del transductor en la entrada inversora de un CFA y por qué funciona la compensación. Este artículo utiliza las técnicas clásicas de retroalimentación para desarrollar un esquema sencillo que añade un único condensador de retroalimentación en paralelo con la resistencia de retroalimentación para compensar la capacitancia de la entrada inversora. El condensador de realimentación introduce un polo no deseado en la respuesta del bucle cerrado, pero el valor del condensador puede ajustarse empíricamente a partir del valor calculado para reducir el efecto limitador de banda del polo.
Te invito a comentar Amplificadores de retroalimentación de corriente en el Comunidad de Diálogo Analógico en EngineerZone.
Referencias
Gray, Paul R., y Robert G. Meyer Análisis y diseño de circuitos integrados analógicos. John Wiley & Sons, Inc, 1977.
Lundberg, Kent. "Sistemas de control por retroalimentación" Notas del curso del M.I.T.
Roberge, James K Amplificador operacional: teoría y práctica. John Wiley & Sons, 1975.
Si quieres conocer otros artículos parecidos a Amplificadores de retroalimentación de corriente de compensación en aplicaciones de fotocorriente puedes visitar la categoría Generalidades.
Deja una respuesta

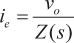
¡Más Contenido!