que es un lugar de raices
Lugar geométrico de las raíces
Considere como forma estándar para la construcción del lugar geométrico de las raíces, la función de transferencia de lazo abierto que da;
[GH(s)=Kfrac{(s+{{z}_{1}})(s+{{z}_{2}})cdots (s+{{z}_{z}})}{(s+{{p}_{1}})(s+{{p}_{2}})cdots (s+{{p}_{p}})}]
donde hay ceros finitos az y polos finitos p de GH(s). Escribimos la ecuación característica del sistema dada a continuación;
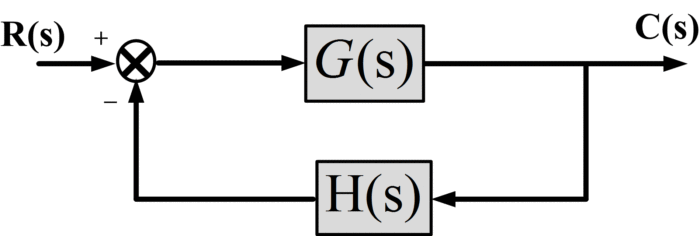
Fig.1: Sistema de circuito cerrado
[frac{C(s)}{R(s)}=frac{G(s)}{1+G(s)H(s)}]
La ecuación característica sería para este sistema de lazo cerrado
$1+G(s)H(s)=0$
O
$G(s)H(s)=-1$
Los polos del lazo cerrado son los valores en los que se cumplen las siguientes dos condiciones condiciones:
Requisito de esquina:
$ángulo G(s)H(s)=pm {{180}^{centerdot }}(2k+1)text{ (k=0,1,3,}cdots text{)}$
Condición de tamaño:
$izquierda| G(s)H(s) right|=1$
Ahora vamos a seguir esbozando un conjunto de pautas para lograr dos goles:
- Encuentra la ubicación del ángulo GH(s) ${{180}^{centerdot }}(2k+1)$.
- Encuentre el valor de K para el cual el tamaño de GH(s) es 1.
- También puedes leer: Teorema de Nyquist | Criterio de estabilidad de Nyquist
Reglas de seguimiento del lugar geométrico de las raíces
1. El número de ramas del lugar geométrico de las raíces es igual al número de polos en lazo cerrado, generalmente el número de polos GH(s).
Cada rama tiene un polo en lazo cerrado para cualquier valor dado de K
2. Cada rama comienza en un polo de lazo abierto de GH(s) (cuando K=0) y termina en cero GH(s) (cuando K=∞)
3. Existirá un lugar geométrico en un punto sobre el eje real cuando la suma del número de polos y ceros sobre el eje a la derecha del punto en cuestión sea impar.
Todos los polos o ceros a la derecha de los puntos de prueba1, el eje real tiene asociado un ángulo de 180 grados. Cuando hay un número impar de polos y ceros a la derecha de s1el ángulo GH(s) será un múltiplo impar de 180 grados.
4. El locus es simétrico con respecto a los hechos.
El hecho proviene de propiedades de las raíces de una ecuación algebraica con coeficientes reales; las raíces complejas deben aparecer en un par conjugado complejo.
5. La suma de las raíces de una ecuación característica es igual al negativo del coeficiente sn-1 donde n es el orden de la ecuación.
Esta guía asume que la ecuación característica se expresa como
${{s}^{n}}+{{a}_{n-1}}{{s}^{n-1}}+{{a}_{n-2}}{{s}^ {n-2}}+ cdots +{{a}_{1}}s+{{a}_{0}}=0$
6. Cuando una rama del lugar geométrico tiende a infinito, tiende a una asíntota cuya dirección es
[{{theta }_{A}}=pm frac{(2k+1)pi }{{{n}_{p}}-{{n}_{z}}}text{ (k=0,}pm text{1,}pm text{2,}cdots text{)}]
donde npags y Nz los polos de bucle abierto y cero son GH(s).
Siete. Las asíntotas interceptan el eje real en un punto dado en
[{{sigma }_{A}}=frac{(sumtext{ of poles})-(sumtext{ of zeros})}{(text{number of poles})-(text{number of zeros})}]
8. El punto en el que el lugar geométrico sale (o entra) del eje verdadero se encuentra cortando y probando.
9. El ángulo en el que el lugar geométrico sale del polo complejo se determina aplicando el criterio de 180 grados.
${{x}_{1}}+{{x}_{2}}={{180}^{centerdot}}$
diez. El criterio de 180 grados determina el ángulo a través del cual el lugar geométrico ingresa al cero complejo.
11Existe una estabilidad limitada cuando el lugar geométrico de las raíces cruza el eje imaginario.
Ejemplo del lugar geométrico de las raíces
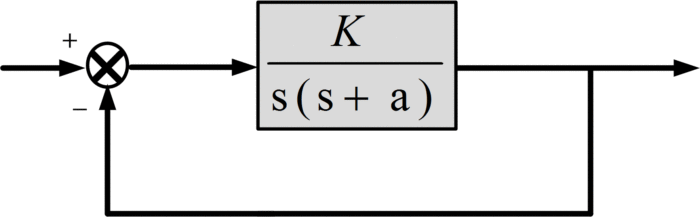
Encuentre el lugar geométrico de los polos del sistema en lazo cerrado para el siguiente sistema
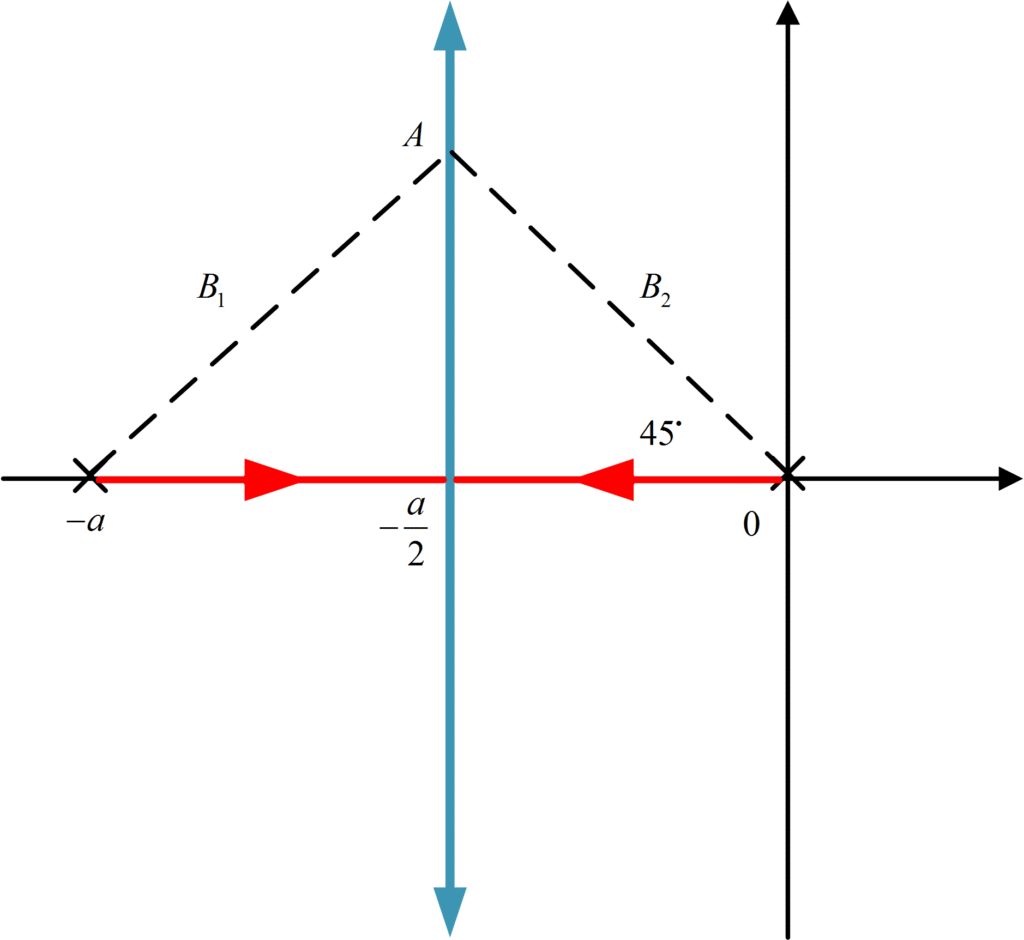
Primero, se dibuja el patrón de polos y ceros de lazo abierto, que consta de polos en el origen y en -a, como se muestra en la figura:
Hay dos polos, por lo que dos ramas de lugar geométrico, comenzando en 0 y -1 para K=0.
Como no hay ceros en el lazo abierto, debe haber dos asíntotas, desde la dirección 6 estarán en +90de y -90de.
Apagado libro guía 7estas asíntotas cruzan el eje real en
[{{sigma }_{A}}=frac{0-a-0}{2-0}=-frac{a}{2}]
Con directriz 3el hecho entre 0 y -a es parte del lugar geométrico, porque está a la izquierda de un polo (impar) en ese eje.
Matlab del lugar geométrico de las raíces
Ahora, hablemos del lugar geométrico de las raíces usando Matlab. Aquí dibujaremos el lugar geométrico de las raíces de la siguiente función de transferencia:
[GH(s)=frac{s+2}{s(s+1)}]
Él es función de transferencia de lazo abiertosin embargo, para graficar un Lugar de Raíces (como mencionamos al principio), debemos Polos de función de transferencia de bucle cerradopuede obtenerse de la siguiente ecuación característica:
[1+KGH(s)=1+Kfrac{s+2}{s(s+1)}=0]
La ecuación característica se puede reescribir de la siguiente manera:
${{s}^{2}}+(1+K)s+2K=0$
Ahora usaremos los coeficientes de la ecuación característica anterior para trazar el lugar geométrico de las raíces usando Matlab.
Diagrama del lugar geométrico de las raíces del código de Matlab
% Matlab Code to Compute Root Locus
% for 1 + K(s+2)/(s(s+1))
clear all; close all;clc
% Numerator and Denumerator for Open Loop Transfer Function
num = [1 2]; den = [1 1 0];
%Display Open-Loop Transfer Function
disp(['L(s) = ', poly2str(num,'s'), '/', poly2str(den, 's')]);
disp(' ');
figure
%Open-Loop Zeros, Plot with o's
olzeros = roots(num)
%Open-Loop Poles, Plot with x's
olpoles = roots(den)
% Plotting Open-Loop Zeros and Poles
plot(real(olzeros),imag(olzeros),'ro'); hold on;
plot(real(olpoles),imag(olpoles),'rx');
% Plot Closed-Loop Poles over Various Values of K
for K = 0.1:0.1:10,
% Root of Characteristics Equation "1+KGH(s)"
closed_poles = roots([1, 1+K, 2*K]);
plot(real(closed_poles),imag(closed_poles),'bx');
end
hold off;
xlabel('Real Axis');
ylabel('Imaginary Axis');
title('Root Locus for Closed Loop Transfer Function');
Resultados
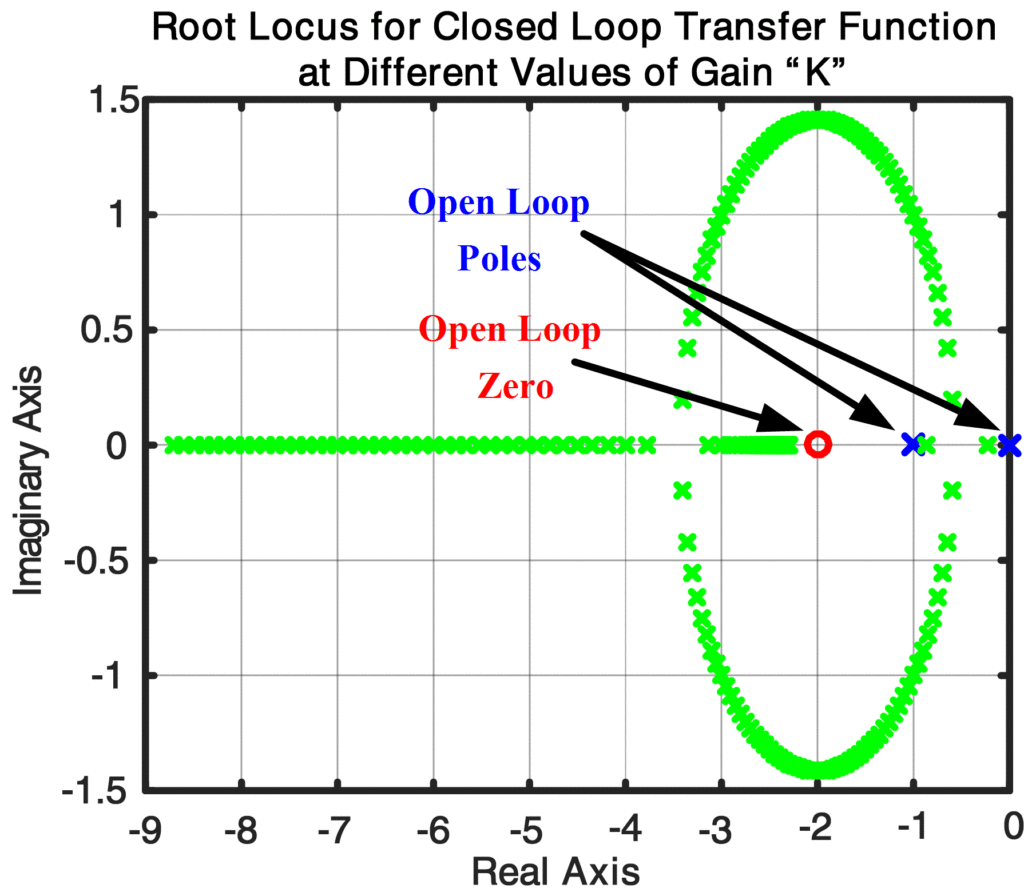
Fig: Raíz del lugar geométrico para la función de transferencia de bucle cerrado a diferentes valores de ganancia de K
El gráfico del lugar de las raíces anterior muestra los polos de la función de transferencia de bucle abierto (en -1 y 0 con azul *) y cero (en -2 con rojo o), así como los polos de la función de transferencia de bucle cerrado en diferentes valores del parámetro de ganancia K de 0,01 a diez.

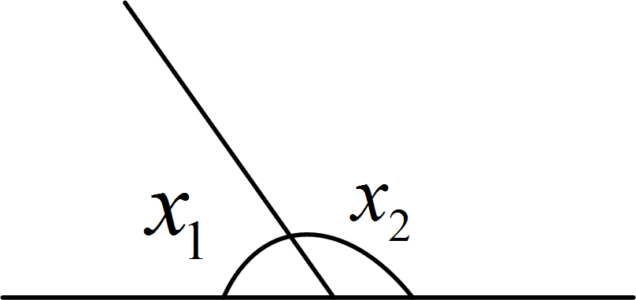
¡Más Contenido!