Principios fundamentales detrás de la topología Sigma-Delta ADC: Parte 1
El Σ-ADC es un elemento básico en el conjunto de herramientas de los diseñadores de sistemas de adquisición y procesamiento de señales de hoy. El objetivo de este artículo es brindar al lector el conocimiento básico sobre los principios fundamentales detrás de la topología Σ-ADC. Se exploran ejemplos de las ventajas y desventajas entre el ruido, el ancho de banda, el tiempo de establecimiento y todos los demás parámetros clave asociados con el diseño del subsistema ADC para brindar contexto a los diseñadores de circuitos de adquisición de datos de precisión.
Por lo general, hay dos bloques: el modulador Σ y el bloque de procesamiento de señal digital, generalmente un filtro digital. Este diagrama de bloques de alto nivel y los conceptos clave del Σ-ADC se muestran en la Figura 1.
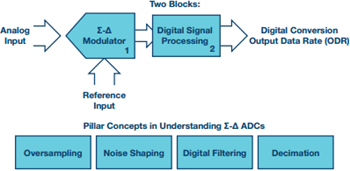
Figura 1. Conceptos pilares del ADC Σ-Δ.
Como el modulador Σ es una arquitectura sobremuestreada, comencemos con la teoría del muestreo y el escenario de Nyquist y la operación de ADC sobremuestreada.
La Figura 2 ilustra la comparación entre la operación de Nyquist de un ADC con el caso sobremuestreado y finalmente con el caso modulado en Σ (también sobremuestreado).
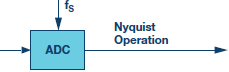
Figura 2. Comparación de Nyquist
La Figura 2a representa el ruido de cuantificación de un ADC cuando se ejecuta en una operación de Nyquist directa. En este caso, el ruido de cuantificación está determinado por el tamaño LSB del ADC. FS es la frecuencia de muestreo del ADC y FS/2 es la frecuencia de Nyquist. La Figura 2b muestra el mismo convertidor, excepto que ahora se usa en un contexto de sobremuestreo, por lo que se emplea una tasa de muestreo más rápida. La frecuencia de muestreo aumenta en un factor de K con el ruido de cuantificación ahora distribuido en un ancho de banda más amplio hasta K × FS/2. El filtro digital de paso bajo (normalmente con diezmado) elimina el ruido de cuantificación fuera de la región azul.

Figura 2a. Escenario de Nyquist. Muestreo en FSel ancho de banda de Nyquist es FS /2.
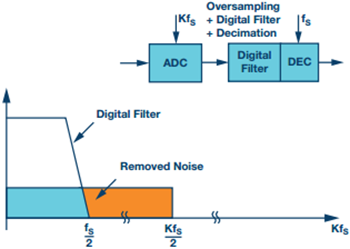
Figura 2b. Escenario sobremuestreado. Muestreo que ocurre en K × FS.
El modulador Σ tiene la característica adicional de dar forma al ruido, como se muestra en la Figura 2c. El ruido de cuantificación de la conversión de analógico a digital está formado por el esquema de modulación, cambiándolo (normalmente) de un ancho de banda bajo a una frecuencia más alta, lo que permite que un filtro digital de paso bajo lo elimine del resultado de la conversión. El Σ-ADC se puede diseñar con el ruido de fondo determinado por el ruido térmico y no limitado por el ruido de cuantificación.
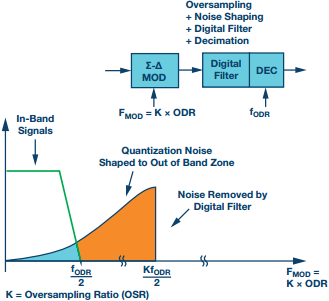
Figura 2c. Escenario ADC Σ-Δ. Sobremuestreado y con forma de ruido, el muestreo ocurre en FMODIFICACIÓN = K × FODR.
Muestrear, modular, filtrar
El Σ-ADC se cronometra utilizando un reloj de muestreo interno o externo. A menudo, el reloj maestro del ADC (MCLK) se divide antes de que el modulador lo use; tenga esto en cuenta cuando lea la hoja de datos del ADC y comprenda la frecuencia del modulador. La frecuencia de muestreo pasada al modulador establece la frecuencia de muestreo FMODIFICACIÓN. El modulador envía datos al filtro digital a esta velocidad, a su vez, el filtro digital (típicamente de paso bajo, con algo de diezmado) proporciona datos a la velocidad de datos de salida (ODR). La Figura 3 ilustra este flujo.
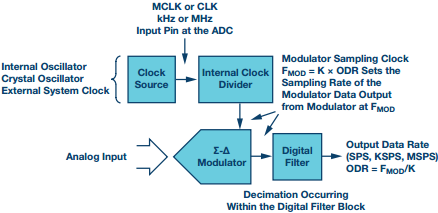
Figura 3. Flujo de ADC Σ-Δ: muestreo desde la salida del modulador hasta la salida filtrada digitalmente.
Vista en profundidad de un modulador Σ de primer orden
El modulador Σ es un sistema de retroalimentación negativa, análogo a un amplificador de bucle cerrado. El bucle contiene un ADC y DAC de baja resolución, así como un filtro de bucle. La salida y la retroalimentación se cuantifican de manera aproximada, a menudo solo una salida de un solo bit como alta o baja. La estructura básica se implementa como un sistema analógico para ADC, donde el cuantificador es el bloque en el que se realiza el muestreo. Siempre que existan condiciones para la estabilidad del bucle, la salida es una representación aproximada de la entrada. El filtro digital toma la salida gruesa y reconstruye una versión digital precisa de la entrada analógica.
En la Figura 4 se ilustra una salida de densidad de unos en respuesta a una entrada de onda sinusoidal. La tasa de cambio de la salida del modulador de un nivel bajo a un nivel alto depende de la tasa de cambio de la entrada. En la entrada de escala completa de la onda sinusoidal, la tasa de conmutación de salida del modulador se reduce y domina el estado de salida +1. De manera similar, cuando la onda sinusoidal está en su escala completa negativa, las transiciones entre +1 y –1 se reducen y domina la salida –1. A la velocidad máxima de cambio de la entrada de onda sinusoidal, se produce la mayor densidad de conmutación entre +1 y –1 en la salida del modulador. La tasa de cambio de la salida sigue a la de la entrada. Es la tasa de transición de la salida del modulador Σ la que describe la entrada analógica.
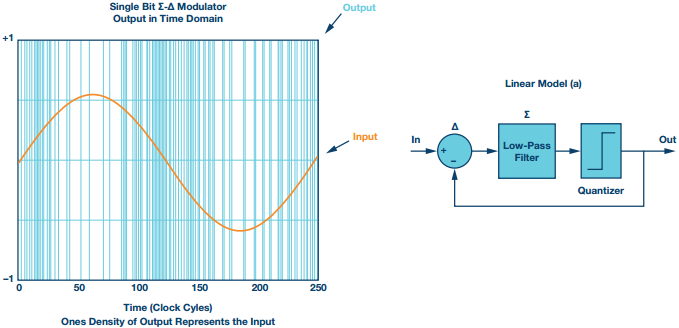
Figura 4. Densidad de Σ-Δ unos en respuesta a la entrada de onda sinusoidal. Modelo lineal (a) del bucle Mod 1 Σ-Δ.
Usando un modelo lineal para describir este modulador de un solo bit (Mod 1), el sistema se muestra como un sistema de control con retroalimentación negativa. El ruido de cuantificación es la diferencia entre la entrada y la salida del cuantificador. Un filtro de paso bajo sigue al nodo delta de entrada. En la Figura 5b, el ruido de cuantificación se describe con el término N.
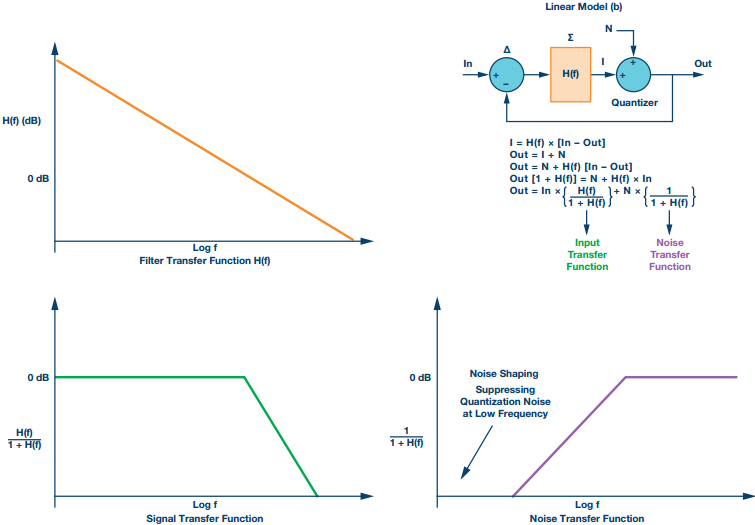
Figura 5. Modelo lineal (b) del bucle Mod 1 Σ- que incluye gráficos de función de transferencia de ecuaciones, filtro, señal y ruido.
H(f) es la función del filtro de bucle y define las funciones de transferencia de señal y de ruido. H(f) es una función de filtro de paso bajo con una ganancia muy alta en frecuencias bajas (dentro del ancho de banda de interés) y atenuación de señales de frecuencia más alta. El filtro de bucle se puede implementar como un integrador simple o como una cascada de integradores. En la práctica, se coloca un DAC en la ruta de retroalimentación para tomar la señal de salida digital y retroalimentarla al nodo delta de entrada analógica.
Resolviendo las ecuaciones que se muestran en la Figura 5 se obtienen las funciones de transferencia de señal y ruido. La función de transferencia de señal opera como un filtro de paso bajo, con una ganancia de 1 en el ancho de banda de interés. La función de transferencia de ruido es una función de filtro de paso alto que proporciona la conformación del ruido. Hay una fuerte supresión del ruido de cuantificación a bajas frecuencias alrededor de la CC. Se incrementa la señal de ruido de cuantificación vista a altas frecuencias fuera del ancho de banda de interés. Para el modulador de orden único (Mod 1), el ruido aumenta a una tasa de aproximadamente 20 dB/década.
Un método común para aumentar la resolución del sistema es aumentar el orden del filtro de bucle colocando en cascada dos filtros de bucle. El H(f) del filtro de bucle general ahora tiene una mayor atenuación y la función de transferencia de ruido tiene una transición de 40 dB/década para un estilo Mod 2. El ruido de cuantificación tiene una forma más agresiva, con un ruido de frecuencia mucho más bajo. La figura 6 compara los ADC Σ Mod 1 y Mod 2. Las variaciones y estilos de los moduladores Σ son muy variados. Las arquitecturas que eluden los problemas de estabilidad de bucles de un solo bit de orden superior se denominan arquitecturas de moduladores de modelado de ruido multietapa (MASH). Las arquitecturas multietapa (estilo MASH) permiten el diseño de moduladores Σ estables de orden alto a través de una combinación de bucles de orden inferior inherentemente estables.
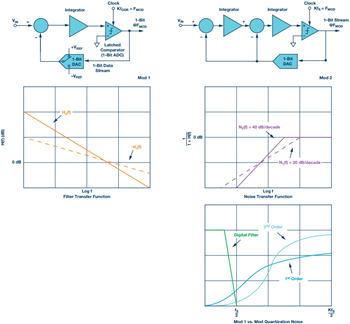
Figura 6. Configuraciones de diagrama de bloques Mod 1 y Mod 2 con gráficos comparativos de las funciones de transferencia de ruido y filtro.
Si quieres conocer otros artículos parecidos a Principios fundamentales detrás de la topología Sigma-Delta ADC: Parte 1 puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!