Resistencias en serie y en paralelo

Los resultados del aprendizaje

• Calcule la resistencia total de diferentes combinaciones de resistencias, es decir, serie, paralelo y serie-paralelo.
• Muestre cómo se usan las resistencias como divisores de voltaje y corriente.
• Calcule el valor de resistencia y potencia para una resistencia de caída de voltaje en serie.

Los resistores individuales se pueden conectar juntos en una conexión en serie, una conexión en paralelo o una combinación de serie y paralelo juntos. Esto da como resultado un circuito más complejo cuya resistencia total del circuito es una combinación de resistencias individuales.

Combinaciones de series de resistencias

Para conectar resistencias i serie, ellos estan conectados de extremo a extremo juntos en una línea como se muestra si Figura 1. Las características de las resistencias conectadas en serie se pueden resumir de la siguiente manera:

• la resistencia total del circuito (R_j( ) aumenta si se conectan resistencias adicionales en serie y disminuye si se quitan las resistencias.
• Para determinar la resistencia total del circuito, simplemente encuentre la suma de las cargas de resistencia individuales.
• En este ejemplo, si las resistencias están etiquetadas R₁, R₂y R₃entonces la resistencia total R_j calcularse mediante la fórmula

Figura 1 Resistencias conectadas en serie.

EJEMPLO 1

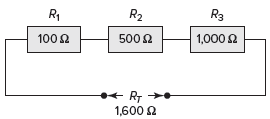
Problema: A través de la resistencia, R₁ (4Ω), R₂ (50Ω), y R₃ (75 Ω) conectados en serie como se muestra i Figura 2. Encuentre el valor de resistencia total del circuito combinado.

Figura 2 Ejemplo de circuito 1.

La solución:

Las resistencias conectadas en serie se utilizan como divisores de voltaje, como se muestra en el circuito imagen 3. Los divisores de voltaje son muy utilizados en circuitos donde una sola fuente de voltaje debe proporcionar varios valores de voltaje diferentes a diferentes partes de un circuito.

Las características de un circuito divisor de voltaje en serie se pueden resumir de la siguiente manera:

• La misma cantidad de corriente fluye a través de cada resistencia.
• El voltaje de entrada se divide proporcionalmente entre las resistencias conectadas en serie.
• La caída de voltaje a través de una resistencia en un circuito en serie es directamente proporcional al valor de resistencia de la resistencia.
• Cuanto mayor sea el valor de la resistencia, mayor será la caída de tensión.

imagen 3 Circuito divisor de tensión.

En el caso de un circuito divisor de tensión, la caída de tensión en cada resistencia suele ser un factor a determinar. La caída de voltaje a través de una resistencia es proporcional a la relación de su valor de resistencia a la resistencia total del circuito.

el es fórmula del divisor de voltaje le permite calcular la caída de voltaje a través de una de las resistencias conectadas en serie sin calcular primero el valor de la corriente del circuito. Expresado como una fórmula:

EJEMPLO 2

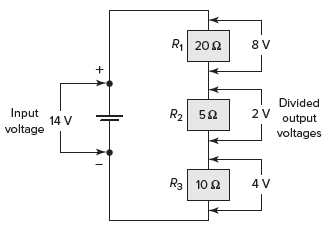
resistencias R₁ (5 kΩ), R₂ (3 kΩ), y R₃ (2 kΩ) conectados en serie para formar un divisor de voltaje como se muestra i Figura 4. Si se aplica un voltaje de entrada de 9 voltios al circuito, calcule el valor de la caída de voltaje en cada una de las resistencias, usando la fórmula del divisor de voltaje.

Figura 4 Ejemplo de circuito 2.

La solución:

EJEMPLO 3

Tiene una fuente de 120 V y desea usar una resistencia de caída en serie junto con una luz de prueba de 6 V 150 mA para indicar cuándo se aplica energía (Figura 5). Determine el valor de la resistencia a la caída en serie y la potencia requerida.

Figura 5 Circuito de ejemplo 3 .

La solución:

Combinación simultánea de resistencias

Las resistencias están conectadas i paralela al conectarlos lado a lado uno al lado del otro, como se muestra en Figura 6. Tenga en cuenta que ambas resistencias están conectadas a los mismos dos puntos.

Las características de las resistencias conectadas en paralelo se pueden resumir de la siguiente manera:

• La resistencia total (R_j) del circuito que lo formaba menos es el valor de resistencia más bajo presente en una de las ramas.
• Cada resistencia proporciona una ruta paralela separada para que fluya la corriente.
• Si tiene varias resistencias del mismo valor al mismo tiempo, la resistencia total se encuentra fácilmente dividiendo el valor de la resistencia común por la cantidad de resistencias conectadas. Para tres resistencias de 150 Ω en paralelo, la resistencia total es

Figura 6 Resistencias conectadas en paralelo.

Para encontrar la resistencia total de dos valores desiguales de resistencias conectadas en paralelo (un uso muy común), se utiliza la fórmula del producto sobre la suma. Esta fórmula es

EJEMPLO 4

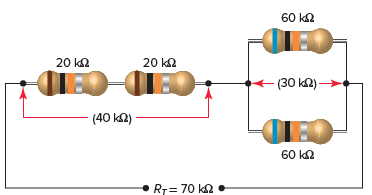
Problema: Una resistencia de 60 Ω está conectada en paralelo con una resistencia de 40 Ω, como se muestra en la figura. Imagen 7. Use la fórmula de producto sobre sumas y encuentre el valor de la resistencia mutua total de los dos.

Imagen 7 Ejemplo circuito 4.

La solución:

La fórmula del producto sobre la suma funciona mejor para dos resistencias en paralelo. Cuando hay más de dos resistencias al mismo tiempo, se vuelve más difícil y menos conveniente de usar. Para más de dos valores de resistencia desiguales conectados en paralelo, se utiliza la fórmula general para la resistencia total de un circuito en paralelo. Esta fórmula es

EJEMPLO 5

Problema: A través de la resistencia, R₁ (120Ω), R₂ (60Ω), y R₃ (40 Ω) conectados en paralelo, como se muestra i Imagen 8. Encuentre el valor de resistencia total del circuito combinado.

Imagen 8 Ejemplo circuito 5.

La solución:

Los circuitos de resistencias en paralelo se pueden considerar como divisores de corriente porque la corriente se divide o se divide entre las diversas resistencias como se muestra i Figura 9.

Las características de un circuito divisor de corriente en paralelo se pueden resumir de la siguiente manera:

• El flujo de corriente a través de cada resistencia de rama es inversamente proporcional a su valor de resistencia.
• Cuanto menor sea el valor de la resistencia, mayor será el flujo de corriente y viceversa.
• Las resistencias con el mismo valor óhmico tendrán la misma cantidad de corriente fluyendo a través de ellas.
• La fórmula que describe un divisor de corriente es similar en forma a la de un divisor de voltaje y se puede expresar como:

Figura 9 Circuito divisor de corriente.

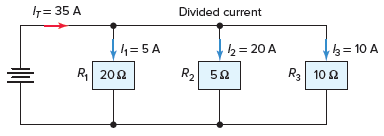
EJEMPLO 6

Problema: resistencias R₁ R₂ y R₃ (2 Ω, 3 Ω y 6 Ω, respectivamente) conectados en paralelo, como se muestra en Imagen 10. Use la fórmula del divisor de corriente para calcular el valor del flujo de corriente a través de cada una de las resistencias de carga si el flujo de corriente total al circuito es de 10 amperios.

Imagen 10 Circuito de ejemplo 6.

La solución:

EJEMPLO 7

Problema: Cuando se conectan cargas adicionales en paralelo, la resistencia total del circuito reducciones Para el circuito mostrado i Una foto 11determine la resistencia total del circuito bajo cada una de las siguientes condiciones de operación:

1. Interruptores 1 y 2 cerrados.
2. Interruptores 1, 2 y 3 cerrados.

Imagen 11 Ejemplo circuito 7.

La solución:

Una combinación serie-paralelo de resistencias

Circuitos combinados resistivos, también conocidos serie-paralelo circuitos resistivos, combine resistencias en serie con resistencias en paralelo, como se muestra en la Imagen 12.

Las reglas que rigen estos circuitos son las mismas que las desarrolladas para los circuitos en serie y en paralelo. Primero, se obtiene la resistencia de resistencia combinada total de la sección paralela. La resistencia total de la sección en paralelo se suma luego a cualquier resistencia en serie para obtener la resistencia total del circuito combinado en serie-paralelo.

Imagen 12 Conexión serie-paralelo de resistencias.

EJEMPLO 8

Problema: Tiene una resistencia de 9 Ω, R₁y una resistencia de 60 Ω, R₂que están conectados en paralelo entre sí y en serie con una resistencia de 40 Ω, R₃como se muestra en el Figura 13. Determine la resistencia total de esta combinación de resistencias en serie-paralelo.

Figura 13 Ejemplo circuito 8.

La solución:

EJEMPLO 9

Problema: Las lecturas de resistencia se pueden usar para verificar los circuitos en busca de condiciones de falla. Como se determinó en el ejemplo anterior, la resistencia total de este arreglo de circuito en serie-paralelo es Imagen 14 Hay 60 ohmios.

1. Averigüe qué valor nuevo es R_j La resistencia debe R₁ tener la culpa apertura aunque los valores de resistencia de R₂ y R₃Siempre lo mismo.
2. Del mismo modo, encuentre cuál es el nuevo valor R_j La resistencia debe R₃ tener la culpa en un cortocircuito aunque los valores de resistencia de R₁y R₂ Siempre lo mismo.

Imagen 14 Ejemplo circuito 9.

La solución:

1. por R₁ en el caso de una falla abierta, el circuito consistiría en R₃ en la serie con R₂ y la resistencia total seria:

1. por R₃ acortado, el circuito consistiría en R₁ paralelo a R₂ y la resistencia total seria:

Preguntas de revisión

1. Calcule la resistencia total para cada uno de los siguientes circuitos de resistencia:
   1. Circuito en serie: R1=40Ω, R2=75Ω
   2. Circuito paralelo: R1=200 Ω, R2=200 Ω, R3=200 Ω
   3. Circuito en serie: R1=2000 Ω, R2=6000 Ω, R3=2200 Ω
   4. Circuito paralelo: R1=14Ω, R2=32Ω
   5. Circuito en serie: R1=4700Ω, R2=800Ω, R3=200Ω
   6. Circuito paralelo: R1=60 Ω, R2=30 Ω, R3=15 Ω
2. resistencias R₁, R₂y R₃ (50 Ω, 30 Ω y 20 Ω, respectivamente) conectados en serie a través de un voltaje aplicado de 200 V para formar un divisor de voltaje. Usando la fórmula del divisor de voltaje, calcule los voltajes mi₁, mi₂y mi₃.
3. La corriente total a través de dos resistencias conectadas en paralelo es de 3 A. hay resistencia R₁ Es de 10 Ω y la resistencia de R₂ es 40 Ω. Usando la fórmula del divisor de corriente, calcule las corrientes yo₁ y yo₂.
4. resistencia de 5 Ω, R₁y una resistencia de 20 Ω, R₂que están conectados en paralelo entre sí y en serie con una resistencia de 6 Ω, R₃. Calcule la resistencia total de este circuito en serie-paralelo.
5. Tienes tres resistencias de 100 Ω para conectar juntas. Describa las tres posibles configuraciones de circuito y calcule sus valores de resistencia total.

Preguntas de revisión - Respuestas

1. (a) 115 Ω, (b) 66,7 Ω, (c) 10200 Ω, (d) 9,74 Ω, (e) 5700 Ω, (f) 8,57 Ω
2. mi₁ = 100 V,E₂ = 60V,E₃ = 40V
3. yo₁ = 2,4 A, yo₂ = 0.6A
4. 10Ω
5. Tres resistencias de 100 Ω conectadas en serie, resistencia total de 300 Ω. Tres resistencias de 100 Ω conectadas en paralelo, resistencia total 33,3 Ω. Dos resistencias de 100 Ω conectadas en paralelo y luego conectadas en serie con una resistencia de 100 Ω, resistencia total de 150 Ω.

• También puedes leer: Capacitores en serie y en paralelo