Qué es un circuito RL : Funcionamiento y usos

La resistencia (R), el inductor (L) y el condensador (C) son los elementos básicos del circuito lineal pasivo. Estos componentes desempeñan un papel fundamental para formar un circuito eléctrico de cuatro formas diferentes, como el circuito RL, el circuito LC y el circuito RLC. Estos circuitos son esenciales en la electrónica analógica, ya que presentan un rendimiento elevado. Generalmente, tanto los condensadores como los inductores son más preferidos en comparación con otros componentes básicos porque su fabricación es muy sencilla. Estos elementos tienen un tamaño reducido para la mayoría de los valores altos de los componentes. Un filtro unipolar puede formarse utilizando los circuitos RL y RC. Cuando los elementos reactivos, como el condensador o el inductor, se conectan en serie/paralelo con la carga, así se determinará si el filtro es de paso alto o de paso bajo. Los circuitos RL se utilizan con frecuencia en los amplificadores de RF, como las fuentes de alimentación de CC, donde el inductor (L) se utiliza para suministrar corriente de polarización de CC y bloquear la RF para que no llegue a la fuente de alimentación.

¿Qué es un circuito RL?

Un circuito RL también se conoce como filtro RL, circuito de resistencia-inductor o red RL, y se puede definir como un circuito que se puede construir con componentes de circuito pasivo como la resistencia y el inductor a través de una fuente de corriente o de tensión. Debido a la existencia de una resistencia R en la forma perfecta del circuito, este circuito utilizará la energía de forma similar a un circuito RC/RLC.

Esto no es como la forma perfecta de un circuito LC, que no utilizará energía debido a la inexistencia de una resistencia. Sin embargo, esto es simplemente la forma perfecta del circuito. En la práctica, incluso un circuito inductor-capacitor utilizará algo de energía debido a la no existencia de resistencia y cables de conexión.
Considera el siguiente circuito RL que incluye una resistencia y un inductor con una alimentación de tensión. Consideremos que el flujo de corriente dentro del circuito es I (amperios) y a través de la resistencia es IR y el inductor es IL correspondientemente.

Como los dos componentes, R y L, están conectados en serie, el flujo de corriente en ambos componentes y en todo el circuito será el mismo: IR = IL = I. La caída de tensión en la resistencia y el inductor son VR y VI

Aplicando la ley de voltaje de Kirchhoff (es decir, la suma de la caída de voltaje debe ser igual a la tensión aplicada) a este circuito, obtenemos,

Una vez aplicada la KVL (ley de tensión de Kirchhoff) al circuito anterior, obtenemos

V = V_R +V_L

Factor de potencia

El circuito RL o circuito de resistencia-inductor es un tipo de circuito eléctrico que puede construirse con resistencias e inductores conectados a una fuente de tensión o corriente. Un circuito RL de primer orden se compone principalmente de una resistencia y un inductor para formar un circuito RL. El factor de potencia de este circuito es bajo debido a la carga inductiva, como un motor de inducción trifásico. Incluso las lámparas, los transformadores y los dispositivos de soldadura funcionan con factores de potencia de retardo bajos.

En el circuito en serie RL, el flujo de corriente va por detrás de la tensión a través de un ángulo "ϕ" debido al efecto inductor. En este caso, el factor de potencia (FP) puede darse como el coseno del ángulo de retardo 'ϕ'

El factor de potencia = Cos ϕ = Resistencia/Impedancia = R/Z

Cos ϕ = R/√R²+X_L² = R/√R²+ (ω _L)²

La ecuación anterior se puede dividir con "R

Cos ϕ = 1/√1+ (ω _L/R)²

De hecho, cuando tenemos ω L>>R, es decir, un factor de potencia pequeño, el "1" del denominador se vuelve insignificante.

Por tanto, Cos ϕ = R/ ω L

Diagrama de fasores

El diagrama fasorial del circuito en serie RL se muestra a continuación:

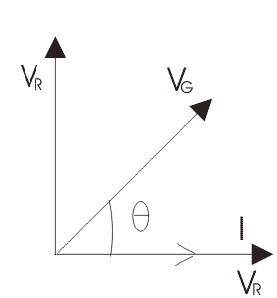
Los siguientes pasos dan instrucciones paso a paso para dibujar el diagrama fasorial.

Aquí se puede tomar como referencia la corriente (I).

La VR, que se conoce como la caída de tensión a través de la resistencia = IR, se puede dibujar en fase a través de la corriente (I).

A través de la reactancia inductiva, la caída de tensión es VL = IXL puede dibujarse por delante del flujo de la corriente porque, el flujo de la corriente retrasa la tensión a través de 90 grados de ángulo dentro del circuito inductivo.
Las dos caídas de tensión del vector son VR y VL, que equivalen a la tensión dada V.

Por lo tanto

En el triángulo anterior como OAB

V_R = I_R y V_L = IX_L donde X_L = 2πfLRL

V = √(V_R)²+ (V_L)²

⁼ √(I_R)²+ (IX_L)²

= I √®²+ (X_L)²

I = L = V/Z

Z = √R² + X_L²

Aquí, "Z" es la resistencia total que se ofrece al flujo de CA a través de un circuito RL en serie. Por tanto, se conoce como la impedancia del circuito RL y se mide en ohmios (Ω).

Ángulo de fase

En un circuito en serie RL, el flujo de corriente se retrasa con respecto a la tensión con un ángulo de 90o que se denomina ángulo de fase

ϕ = tan-1 (X_L/R)

La impedancia del circuito RL en serie

La impedancia del circuito RL en serie se opone al flujo de corriente y no es más que la combinación del efecto de la resistencia (R) y la reactancia inductiva (XL) de todo el circuito. La impedancia 'Z' en ohmios puede darse como la siguiente.

Z = (R² + XL^2)0.5

A partir del triángulo rectángulo de las siguientes imágenes, el ángulo de fase ϕ = tan^-1 (X_L/R).

Circuito paralelo RL

Cuando tanto la resistencia como el inductor se conectan en paralelo entre sí y se alimentan a través de una fuente de tensión, se conoce como circuito paralelo RL. Las tensiones de entrada y salida del circuito son Vin y Vout. Una vez que la resistencia y el inductor están conectados en paralelo, Vin es equivalente a Vout. Sin embargo, el flujo de corriente dentro de estos componentes no es el mismo.

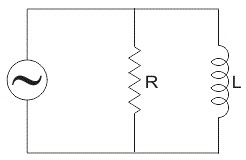
Este tipo de circuito no se puede utilizar como filtro de tensiones porque las tensiones de entrada y salida de este circuito son iguales. Por esta razón, este circuito no se utiliza con frecuencia en comparación con el circuito RL en serie.

Diagrama de fasores

En un circuito RC en paralelo, la relación principal entre la tensión y las corrientes puede ilustrarse mediante el diagrama vectorial (fasorial).

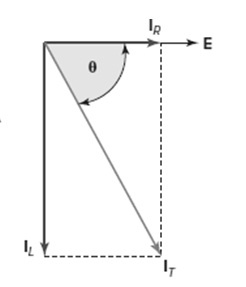
• El vector de referencia "E" & significa la tensión dentro del circuito paralelo RL.
• Como el flujo de corriente a lo largo de la resistencia está en fase con la tensión a través de ella, entonces el IR se muestra en el vector de tensión.
• La "IL" se retrasa respecto a la tensión en un ángulo de 90 grados y puede disponerse en dirección descendente para retrasar el vector de tensión en un ángulo de 90 grados.
• Aquí, la adición de ambos vectores, como el IR y el IL, proporciona un resultado que significa la suma (IT) de la corriente de línea
• El ángulo "θ" denota la fase entre la corriente y la tensión de línea dadas.
• A continuación se muestra el diagrama fasorial del circuito RL en paralelo.

En el caso de un circuito en paralelo, el flujo de corriente dentro de cada rama de un circuito actúa independientemente de las corrientes dentro de las ramas restantes. El flujo de corriente en cada rama puede determinarse mediante la tensión a través de la rama y la resistencia al flujo de corriente en forma de reactancia inductiva o resistencia incluida dentro de la rama.

La corriente en cada rama puede determinarse mediante la ley de ohmios

I_R = E/R

I_L = E/X_L

El flujo de corriente dentro de la rama resistiva incluye una fase similar a la de la tensión dada; sin embargo, la corriente en una rama inductiva va por detrás de la tensión dada con 90 grados de ángulo. En consecuencia, la corriente de toda la línea incluye IR e IL con 90 grados de desfase entre sí.

El flujo de corriente en ambos componentes puede formar los catetos de un triángulo rectángulo y la corriente total es la hipotenusa. Por tanto, se utiliza el teorema de Pitágoras para incluir estas corrientes juntas mediante la siguiente ecuación:

I_T = √I_R² + I_L²

En estos circuitos, el ángulo de fase en el que toda la corriente va por detrás de la tensión está entre 0 y 90 grados. Por tanto, el tamaño del ángulo puede determinarse mediante la existencia de una corriente inductiva adicional o de una corriente resistiva.

Si hay una corriente inductiva adicional, el ángulo de fase "θ" estará más cerca de los 90 grados. Estará más cerca de cero grados si hay una corriente resistiva adicional. Por tanto, a partir del diagrama vectorial del circuito anterior podemos observar que el valor del ángulo de fase puede medirse a partir de la siguiente ecuación:

Θ = tan-1 (I_L/I_R)

Impedancia

La impedancia de un circuito RL paralelo puede definirse como la resistencia total hacia el flujo de corriente. Comprende la resistencia que se ofrece desde la rama resistiva "R", así como la reactancia inductiva "XL" que puede ofrecerse a través de la rama inductiva.

La impedancia del circuito RL paralelo puede calcularse como la de un circuito resistivo paralelo. Pero, como R y XL son magnitudes vectoriales, deben incluirse vectorialmente. En consecuencia, la ecuación de la impedancia de un circuito RL paralelo incluye una única resistencia e inductor, por lo que la fórmula de la impedancia de un circuito RL paralelo es

Z = RX_L/√R² + XL²

En el denominador de la ecuación anterior está la suma vectorial de la resistencia y la inductancia. Por lo tanto, si hay más de una rama resistiva e inductiva, deben ser equivalentes para toda la resistencia o reactancia de estas ramas paralelas.

Una vez que se conocen la corriente total y la tensión aplicada, la impedancia puede medirse de forma más sencilla mediante la ley de Ohm, como se indica a continuación.

Z = E/I_T

La impedancia del circuito RL en paralelo es siempre baja en comparación con la resistencia o la reactancia inductiva de cualquier rama. Por esta razón, cada rama forma una vía separada para el flujo de corriente, por lo que disminuye la resistencia de todo el circuito hacia el flujo de corriente.

Cuando la rama tiene la mayor cantidad de corriente, es la que más afecta al ángulo de fase. Por tanto, esto es inverso a un circuito RL en serie.

En un circuito RL en paralelo, si la inductancia es mayor que la resistencia, la corriente de la rama resistiva es superior a la inductiva. En consecuencia, el ángulo de fase entre la tensión dada y la corriente total puede estar más cerca de 0 grados porque es más sensible dentro de la naturaleza.

Usos del circuito RL

Los componentes básicos, como las resistencias, los condensadores y los inductores, se combinan para formar diferentes circuitos, como los circuitos RC, RL y RLC. Las aplicaciones de los circuitos RL, RC y RLC son las siguientes

• Amplificadores de RF
• Sistemas de comunicación
• Circuitos de filtrado
• Procesamiento de la señal
• Circuitos de oscilación
• Aumento de la corriente o la tensión
• Circuitos de sintonía variable
• Transmisores de ondas de radio
• Circuito LC Resonante/Circuito RLC
• Estos circuitos se utilizan como fuentes de alimentación de CC dentro de los amplificadores de RF porque el inductor (L) se utiliza para suministrar corriente de polarización de CC y bloquear la RF para que llegue a la fuente de alimentación.

Por tanto, se trata de una visión general del Circuito RL, circuito RL en serie, circuito RL en paralelo, diagrama fasorial, y sus usos. Aquí tienes una pregunta, ¿cuáles son las ventajas de los circuitos RL?