LTspice: análisis de circuitos en el peor de los casos con ejecuciones mínimas de simulaciones
Al diseñar un circuito en LTspice, es posible que desee evaluar el impacto de las tolerancias de los componentes. Por ejemplo, el error de ganancia introducido por resistencias no ideales en un circuito de amplificador operacional. Este artículo ilustra un método que reduce la cantidad de simulaciones necesarias y, como resultado, acelera el tiempo de obtención de resultados.
LTSpice proporciona varias formas de variar el valor de un parámetro. Algunos de estos son:
- .parámetro de paso; Un barrido de parámetros de una variable definida por el usuario
- gauss(x); Un número aleatorio de distribución gaussiana con un sigma de x
- plano (x); Un número aleatorio entre -x y x con distribución uniforme
- mc(x,y); Un número aleatorio entre x*(1+y) y x*(1-y) con distribución uniforme.
Estas funciones son muy útiles, especialmente si queremos ver los resultados en términos de una distribución. Pero si solo queremos observar las peores condiciones, es posible que no sean la forma más rápida de obtener un resultado. Usando gauss(x), plano(x) y mc(x,y) por ejemplo, requerirá una simulación para ejecutarse un número estadísticamente significativo de veces. A partir de ahí, se puede observar una distribución y calcular los valores del peor de los casos en términos de desviaciones estándar. Sin embargo, para un análisis del peor de los casos, preferiríamos no utilizar un enfoque de distribución, sino que en los cálculos se utiliza la desviación máxima del valor nominal de cada componente.
Digamos que queremos ver el impacto en el peor de los casos de un R1 = 22,5 kΩ resistencia con un 1% tolerancia. En este caso, solo queremos ejecutar la simulación con R1 = 22,5 kΩ * (1 - 0,01) y 22,5 kΩ * (1 + 0,01). Una tercera carrera con un ideal 22,5 kΩ resistencia también sería útil tener.
Lista de parámetros R1 de .step 22.5k*(1-.01) 22.5k*(1+.01) 22.5k
Si solo estuviéramos variando un valor de resistencia, el método '.step param' funcionaría muy bien. Pero, ¿y si tenemos más? El amplificador diferencial clásico tiene 4 resistencias.
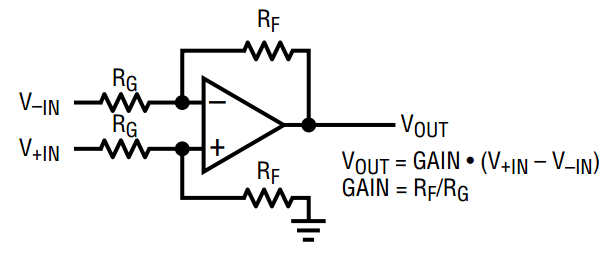
Figura 1. Configuración del amplificador de diferencia (de la hoja de datos LT1997-3)
Si se diseñara un amplificador diferencial discreto, cada uno de estos tendría cierta tolerancia (por ejemplo, 1% o 5%).
Como ejemplo, tomemos la aplicación de la página principal que se muestra en la hoja de datos LT1997-3 e implementémosla en LTspice con un amplificador operacional discreto LT6015 y algunas resistencias no ideales.

Figura 2. Ejemplo de aplicación de la página principal de LT1997-3

Figura 3. Amplificador diferencial LT6015 con resistencias no ideales
Observe que los valores de las resistencias R1, R2, R3 y R4 se reemplazan por una llamada de función wc(valor nominal, tolerancia, índice) que se define en la simulación por un .función declaración:
.func wc(nom,tol,index) if(run==numruns,nom,if(binary(run,index),nom*(1+tol),nom*(1-tol)))
Esta función junto con la binario (ejecutar, índice) La siguiente función varía el parámetro para cada componente entre su valor máximo y valores mínimos y para la última ejecución el valor nominal.
.func binary(ejecutar,índice) piso(ejecutar/(2**índice))-2*piso(ejecutar/(2**(índice+1)))
los binario función alterna cada índice'ed componente en la simulación para que todas las combinaciones posibles de nom*(1+tol) y nom*(1-tol) son simulados. Tenga en cuenta que el índice de componentes debe comenzar con 0. La siguiente tabla destaca el funcionamiento del binario() función con resultados para cada índice y correrdonde 1 representa nom*(1+tol) y 0 representa nom*(1-tol).
| Correr | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Índice 0 (R4) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Índice 1 (R1) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Índice 2 (R2) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Índice 3 (R3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
El número de carreras se determina comprar 2norte +1dónde norte es igual al número de componentes indexados, para cubrir todas las combinaciones máximas y mínimas del dispositivo más el nominal. En nuestro caso necesitamos 17 Las simulaciones se ejecutan y podemos definir esto usando el .paso comando y el .parámetro declaración:
.paso parámetro ejecutar 0 16 1
.param numruns=16
Por último, necesitamos definir la tola y tolb para la simulación a través de .parámetro declaración:
.param tola=.01
.param tolb=.05
Puede encontrar más información sobre el .función, .paso, y .parámetro declaraciones en la ayuda (F1) y en el .parámetro detalles de la sección sobre el si(x,y,z) y piso(x) funciones
Si se ejecuta la simulación de análisis transitorio, consulte el archivo WorstCase_LT6015.asc, podemos observar nuestros resultados. Para una corriente de prueba de 250 mA, esperamos que la red Vout se estabilice en 250 mV. Pero ahora con nuestro WC() función, obtenemos una extensión de 235mV a 265mV.

Figura 4. Análisis de transitorios de amplificador de diferencia
En este punto, podríamos acercarnos y observar la dispersión de pico a pico. Pero tomemos una lección de otro blog de LTspice:
Trazado de un parámetro contra algo que no sea el tiempo (por ejemplo, resistencia)
Este blog cubre cómo ejecutar una simulación varias veces y trazar un parámetro contra algo que no sea el tiempo. En este caso, queremos trazar el índice V(out) frente a la ejecución de la simulación. Consulte WorstCase_LT6015_meas.asc expediente.
En esta simulación hemos agregado un archivo .medida Declaración para calcular el voltaje promedio de la salida.
.meas VoutAvg promedio V (salida)
Para trazar el parámetro V(out) vs. run, podemos ver el Registro de errores de SPICE (Ctrl-L), clic derecho y seleccione Trazar datos .step'ed .meas.

Figura 5. Interfaz de registro de errores de Spice
Los resultados de la trama de nuestro .paso'ed.medida datos.

Figura 6. Voltaje de salida frente a ejecución de simulación
La traza nos muestra que los resultados varían desde un peor caso máximo de 265 mV (ejecución 9) hasta un caso peor mínimo de 235 mV (ejecución 6) o aproximadamente un error de ±6 %. Esto tiene cierto sentido intuitivo ya que teníamos resistencias de 1% y 5% en este ejemplo. La última ejecución (16) muestra el resultado ideal (250 mV), que son resistencias ideales. Recall LTspice grafica los resultados del .medida declaración como un gráfico lineal por partes.
Otro enfoque más rápido para este circuito en particular es usar el .op simulación (en lugar de .trans) para realizar una solución de punto de operación de CC que trazará los resultados de nuestro paso.medida datos directamente.
Cuando se diseña un amplificador diferencial, no solo se necesita el amplificador operacional apropiado, sino que igualmente importante es la coincidencia de las resistencias. Las siguientes referencias hacen un excelente trabajo al explicar este tema (y las matemáticas asociadas) en detalle:
Sin embargo, no se puede lograr una buena relación de rechazo de modo común (CMRR) ni un error de ganancia sin las resistencias correspondientes.
Linear Technology, que ahora forma parte de Analog Devices, tiene varios productos amplificadores de precisión que también incluyen resistencias adaptadas. Un ejemplo recientemente lanzado de esto es el LT1997-3 - Amplificador seleccionable de ganancia de amplio rango de voltaje de precisión. Dos especificaciones clave son:
- CMRR CC mínimo de 91 dB (ganancia = 1)
- 0,006 % (60 ppm) Error de ganancia máxima (Ganancia = 1)
Estas especificaciones son realmente excelentes. De acuerdo con DN1023, CMRR debido solo a resistencias del 1% (con un amplificador operacional ideal) limitará su CMRR a 34dB. Y, por supuesto, el error de ganancia es mucho peor que lo que logra el LT1997-3.
Con el método descrito anteriormente, se puede ejecutar un análisis simple del peor de los casos con el valor mínimo/máximo de varios parámetros. En este ejemplo, observamos el impacto de las tolerancias de las resistencias en un amplificador diferencial clásico, y se ilustra el valor de las resistencias adaptadas en el LT1997-3.
Referencias
Análisis de circuito Monte Carlo y en el peor de los casos con LTSpice
Si quieres conocer otros artículos parecidos a LTspice: análisis de circuitos en el peor de los casos con ejecuciones mínimas de simulaciones puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!