Cuando la corriente cruza el conductor, un campo electromagnético lo rodea. Este campo tiene una propiedad llamada resultado inductancia (L), que se opone a cualquier modificación de la actual. Los inductores son componentes diseñados para tener esta propiedad. En este módulo, analizaremos la construcción básica de los inductores, cómo se pueden combinar en serie y en paralelo, y cómo se comportan en los circuitos.
A un inductor es un componente eléctrico, formado por una bobina de alambre, que exhibe la propiedad de inductancia. La cantidad de inductancia de una bobina se mide i Enrique (M).
Un Henry se define como la tasa de cambio de corriente de un amperio por segundo inducida por un voltio a través de la bobina.
Sin embargo, el henrio es una unidad relativamente grande y la inductancia a menudo se mide en milihenrios (mH) o microhenrios (µH).
Estructura básica de un inductor
La Figura 1 muestra un inductor básico con líneas magnéticas de fuerza y dirección de corriente. La cantidad de corriente que fluye a través de la bobina es proporcional a la magnitud del campo; por lo tanto, una corriente cambiante provocará un campo magnético cambiante alrededor del inductor. Este campo variable es la causa de la voltaje inducido a través de la bobina. Este voltaje está en dirección opuesta a la corriente y es lo que se opone al cambio de corriente.
Figura 1 - Inductor básico
El material que rodea el cable tiene un gran efecto en la inductancia de una bobina. El contenido interno, llamado corazón, pueden ser no magnéticos (aire, madera, etc.) o magnéticos (hierro, acero, etc.). el es permeabilidad El núcleo es una medida de su resistencia a las líneas de fuerza magnéticas. Dado que las líneas de control de fuerza en la cantidad de la inductancia, la permeabilidad del núcleo (µ) está directamente relacionada con la inductancia.
Otras características del inductor que controlan la cantidad de inductancia son la sección transversal del núcleo (A), el número de vueltas en la bobina (N) y longitud de bobina (l). La inductancia se encuentra mediante la siguiente fórmula:
[L=frac{{{N}^{2}}times mu times A}{l}]
Otras dos características de los inductores son la resistencia del devanado y la capacitancia del devanado. el es Resistencia al viento es la medida de la resistencia de corriente continua del cable que es la bobina. el es capacidad de bobinado hay un efecto secundario debido a las múltiples vueltas del cable adyacente. Estos pueden afectar un circuito si la inductancia es extremadamente grande o la frecuencia es extremadamente alta; sin embargo, en la mayoría de los circuitos estos pueden ignorarse en los cálculos.
Determine la inductancia de la bobina a partir de los siguientes valores:
NO = 350, µ = 0,25 × 10-3 h/m yo = 1,5 cm, diámetro central = 0,5 cm
Primero, encuentre el área del núcleo; luego, inserte los valores dados en la ecuación de inductancia para obtener la respuesta:
$A=pi {{r}^{2}}=pi times {{0,005}^{2}}=1,96times {{10}^{-5}}{{m}^{2} ps
$L=frac{{{N}^{2}}times mu times A}{l}=frac{{{left( 350 right)}^{2}}left( 0.25 veces {{10}^{-3}} right)left( 1,96 times {{10}^{-5}} right)}{left( 0,015 right)}=40mH$
Inductores en serie
La imagen en su cabeza de varios inductores conectados de punta a punta. Si los acerca más y más, se verán como un gran carrete de hilo. Así es como funciona un circuito inductivo en serie. Los inductores en serie simplemente se suman para formar un inductor más grande. La fórmula para encontrar la inductancia en serie total es similar a la resistencia en serie total.
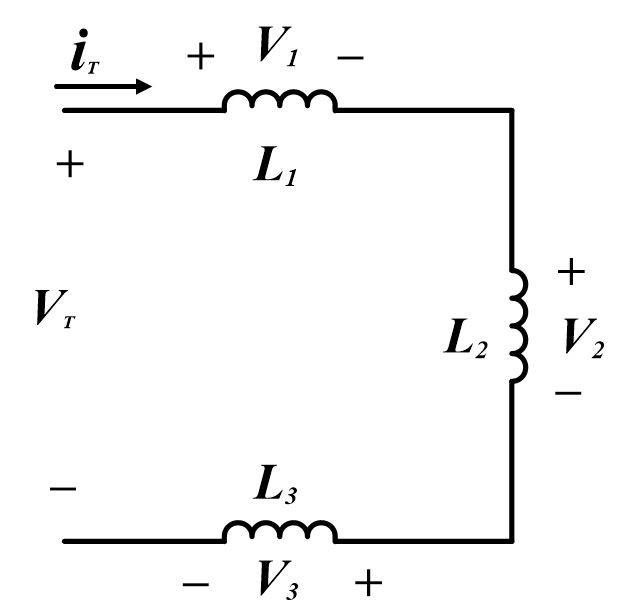
El método para determinar la inductancia total del siguiente circuito es similar al que se usa para las resistencias en serie. De acuerdo con la ley de voltaje de Kirchhoff, podemos escribir la siguiente ecuación para la siguiente figura:
${{V}_{T}}={{V}_{1}}+{{V}_{2}}+{{V}_{3}}text{ }cdotstext{ ( a)}$
La corriente que fluye en el circuito es ij. $frac{d{{i}_{t}}}{dt}$ es la tasa de cambio de la corriente que fluye en el circuito.
Dividiendo ambos lados de la ecuación (a) por $frac{d{{i}_{t}}}{dt}$ se obtiene la siguiente expresión:
[frac{{{V}_{T}}}{{}^{d{{i}_{t}}}/{}_{dt}}=frac{{{V}_{1}}}{{}^{d{{i}_{t}}}/{}_{dt}}+~frac{{{V}_{2}}}{{}^{d{{i}_{t}}}/{}_{dt}}+frac{{{V}_{3}}}{{}^{d{{i}_{t}}}/{}_{dt}}text{ }cdots text{ (b)}]
El lado izquierdo de la ecuación (b) es el voltaje total dividido por la tasa de cambio de la corriente. Este término da la inductancia total Lj. Cada término en el lado derecho de la ecuación (b) da el valor de un inductor individual:
[frac{{{V}_{1}}}{{}^{d{{i}_{t}}}/{}_{dt}}={{L}_{1}}]
[frac{{{V}_{2}}}{{}^{d{{i}_{t}}}/{}_{dt}}={{L}_{2}}]
[frac{{{V}_{3}}}{{}^{d{{i}_{t}}}/{}_{dt}}={{L}_{3}}]
Por lo tanto, la inductancia total sería,
${{L}_{T}}={{L}_{1}}+{{L}_{2}}+{{L}_{3}}text{ }cdotstext{ ( c)}$
La ecuación (c) establece que cuando los inductores están conectados en serie, la inductancia total es la suma de las inductancias individuales.
Si hay dos o más inductores de igual valor en serie, la inductancia total se puede encontrar mediante;
${{L}_{T}}=NL$
Donde N es el número de inductores iguales y L es el valor del inductor individual.
Inductores en paralelo
Los inductores también se pueden combinar en circuitos paralelos. La conexión de inductores en serie aumenta la inductancia total; por lo que está claro que las inductancias de enlace deberían disminuir en paralelo con la inductancia total.
Así como los inductores en serie actúan como resistencias en serie, los inductores en paralelo actúan como resistencias en paralelo. La fórmula para encontrar la inductancia total en un circuito en paralelo es muy parecida a la fórmula para la resistencia total en un circuito en paralelo.
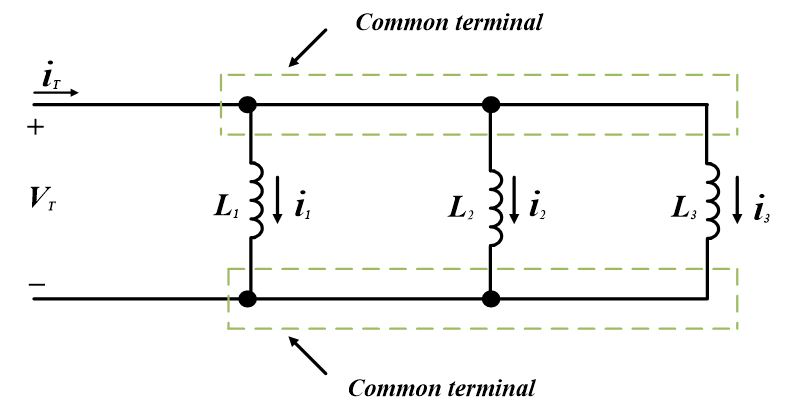
Al aplicar la ley de corriente de Kirchhoff a la siguiente figura, podemos determinar cómo se combinan los inductores paralelos;
$~{{i}_{T}}={{i}_{1}}+{{i}_{2}}+{{i}_{3}}text{ }cdots text{ (d)}$
Para expresar la ecuación anterior como la tasa de cambio de corriente, tome la derivada de ambos lados;
[frac{d{{i}_{T}}}{dt}=frac{d{{i}_{1}}}{dt}+frac{d{{i}_{2}}}{dt}+frac{d{{i}_{3}}}{dt}text{ }cdots text{ (e)}]
Dado que el voltaje a través de un inductor
${{V}_{L}}=Lfrac{di}{dt}$
Y también de Vj el voltaje total a través del inductor paralelo es,
$frac{{{V}_{T}}}{{{L}_{T}}}=frac{{{V}_{T}}}{{L}_{1}}} + frac{{{V}_{T}}}{{{L}_{2}}+frac{{{V}_{T}}}{{L}_{3}}} text{ }cdots text{ (f)}$
Dividiendo ambos lados de la ecuación (c) por Vj la siguiente ecuación nos daría;
$frac{1}{{{L}_{T}}}=frac{1}{{{L}_{1}}}+frac{1}{{L}_{2}}} + frac{1}{{{L}_{3}}}text{ }cdots text{ (g)}$
La ecuación (g) establece que el recíproco de la inductancia total es igual a la suma de los recíprocos de los inductores individuales conectados en paralelo.
Si dos o más inductores paralelos son iguales. La inductancia total se puede determinar dividiendo el valor de uno de los inductores por el número de inductores equivalentes.
${{L}_{T}}=frac{L}{N}$
Mientras que L es el valor de uno de los indicadores iguales y N es el número de inductores iguales.
Nuevamente, imagine múltiples inductores conectados entre sí, excepto que esta vez están en paralelo. En un circuito en paralelo, la corriente se distribuye entre las ramas; por lo tanto, fluye menos corriente a través de cada inductor. Esto da como resultado menos voltaje inducido, lo que resulta en menos inductancia total.
Energía almacenada en un inductor
Es la potencia que ingresa a un inductor en cualquier instante;
$P=Vi=Lifrac{di}{dt}$
Cuando la corriente es constante, la derivada es cero y no se almacena energía adicional en el inductor. Cuando la corriente aumenta, la derivada de corriente tiene un valor positivo y la potencia es positiva. La energía total en el inductor en cualquier instante dado es la potencia central desde menos infinito hasta ese instante;
${{W}_{L}}=underset{-infty }{overset{t}{matopint }},Vi~dt=underset{-infty}{overset{t} {matopint}},Lifrac{di}{dt}dt$
porque sabemos que
$iizquierda(-inftyderecha)=0$
Asi que,
${{W}_{L}}=underset{0}{overset{i}{matopint }},Li~di$
Después de la integración, tenemos la expresión final de energía;
${{W}_{L}}=frac{1}{2}L{{i}^{2}}text{ }cdots text{ (h)}$
OhL= energía almacenada en el inductor en el tiempo t en Joules
yo = la corriente en la inductancia en el tiempo t en amperios
La ecuación (e) muestra que la energía total en el inductor depende solo del valor instantáneo de la corriente. Para que la energía almacenada en el inductor, dada por la ecuación (e), sea positiva, la corriente y el voltaje deben tener signos consistentes, como se muestra en la siguiente figura:
También puedes leer:
Resistencias en serie y en paralelo
Condensadores en serie y en paralelo


¡Más Contenido!