Diagrama fasorial y álgebra fasorial utilizados en circuitos de CA

Figura 1 muestra un circuito en serie de CA simple que consta de una resistencia y un inductor. La fuente del voltaje sinusoidal hace que una onda sinusoidal de corriente fluya a través del circuito. Dado que todos los componentes están conectados en serie, la corriente en el inductor siempre debe ser la misma que la corriente en la resistencia.

De hecho, las corrientes sinusoidales en el inductor y en la resistencia son las mismas, por lo que podemos representar ambas con el símbolo de la letra i.

Figura 1 Circuito AC con resistencia e inductancia en serie

La onda semilla actual a través de la resistencia crea una caída de voltaje sinusoidal que está exactamente en fase con la onda semilla actual.

La corriente instantánea a través del inductor reduce el voltaje instantáneo que se le aplica en π/2 radianes. Por lo tanto, el voltaje sinusoidal en el inductor y el voltaje sinusoidal en el resistor están desfasados ​​por π/2 radianes, y el voltaje instantáneo en el inductor alcanza su pico positivo π/2 radianes antes que el voltaje instantáneo en el resistor.

La ley de voltaje de Kirchhoff establece que la suma de los voltajes en un circuito en serie debe ser igual al voltaje aplicado. En los circuitos de CC donde el voltaje de la fuente es independiente del tiempo, la suma de las caídas de voltaje se puede encontrar mediante aritmética simple.

Ahora necesitamos encontrar la suma de dos voltajes sinusoidales desplazados de fase. Un voltaje sinusoidal se puede representar por su valor instantáneo, v = V_metro sen ωt o su valor RMS, V = 0,707 V_metro.

Debido a que el valor instantáneo cambia continuamente y depende del pasado, se dice que pertenece al dominio del tiempo. En el dominio del tiempo, la distancia angular recorrida por una sinusoide se expresa en radianes. Podemos usar álgebra ordinaria para cálculos con valores instantáneos.

Dado que el valor RMS de una onda extendida no cambia con el instante exacto en el tiempo, tratamos un voltaje alterno sinusoidal como una cantidad fasorial que tiene una amplitud y un ángulo de fase. Se dice que tales cantidades pertenecen a la dominio de la frecuencia. Los cálculos con pasadores requieren una forma especializada de álgebra, que se describe más adelante en este capítulo.

Adición de valores instantáneos

Dado que la ley de voltaje de Kirchhoff se aplica al circuito i Figura 1 cada minuto,

[begin{matrix}e={{v}_{T}}={{v}_{R}}+{{v}_{L}} & {} & left( 1 right) end{matrix}]

Por tanto, podemos sumar los valores instantáneos de las ondas sinusoidales por simple suma aritmética. Aunque la suma de los voltajes instantáneos no nos da una imagen completa de la suma de las ondas totales, podemos repetir el cálculo a intervalos durante un ciclo completo para determinar la naturaleza de la onda resultante.

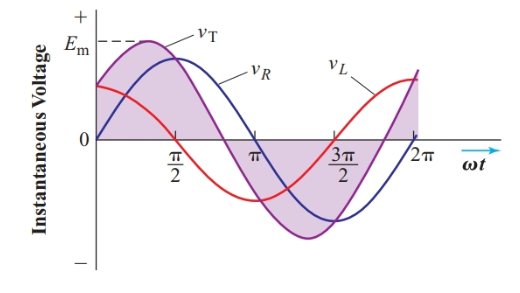
Para facilitar esta tediosa tarea, podemos trazar las curvas sinusoidales de ambos conjuntos de valores instantáneos en el mismo gráfico, como en Figura 2. Dado que la velocidad angular es constante para una frecuencia determinada, podemos mostrar el ángulo de fase de la fuente, ωt, en lugar del tiempo en el eje horizontal.

Figura 2 Se agregaron dos ondas sinusoidales desfasadas

En t=0, el voltaje instantáneo a través de la resistencia es cero; por lo tanto, el valor instantáneo del voltaje total es el mismo que el voltaje a través del inductor en ese instante.

Con el tiempo, el voltaje instantáneo a través del inductor disminuye y el voltaje instantáneo a través de la resistencia aumenta. Aproximadamente a 1 rad, su suma alcanza su valor máximo. En π/2 rad, el voltaje instantáneo en las terminales del inductor es cero y el valor instantáneo del voltaje total es igual al voltaje instantáneo en las terminales del resistor.

Aproximadamente 1 rad más tarde, los valores instantáneos de los voltajes a través de la resistencia y el inductor son iguales en magnitud pero opuestos en polaridad, por lo que v_j = 0.

Consideración cuidadosa de Figura 2 muestra que la forma de onda para v_j es una sinusoide con el mismo periodo que v_R y v_L. De hecho, cualquier suma de ondas sinusoidales de la misma frecuencia tiene esta propiedad.

Una onda sinusoidal con la misma frecuencia es la suma de ondas sinusoidales con la misma frecuencia.

Ecuación 1 se puede extender a

[begin{matrix}e={{V}_{mR}}sin omega t+{{V}_{mL}}sin left( omega t+{}^{pi }/{}_{2} right) & {} & left( 2 right) end{matrix}]

Ya que v_R y v_L no alcanzan sus valores máximos al mismo tiempo, el valor máximo de v_j ocurre en un momento en que los valores instantáneos de los voltajes de los dos componentes son más bajos que sus valores pico. Por lo tanto,

[{{E}_{m}}ne {{V}_{mR}}+{{V}_{mL}}]

Dado que el valor RMS de cualquier onda extendida es igual al valor máximo dividido por $sqrt{2}$,

[Ene {{V}_{R}}+{{V}_{L}}]

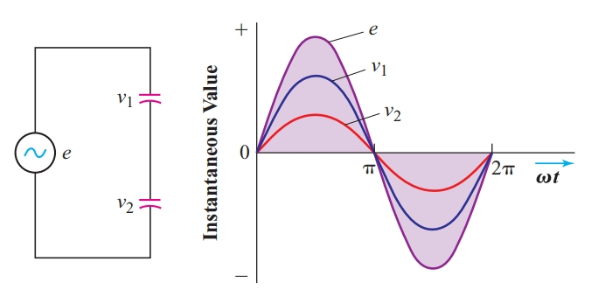
Por lo tanto, la suma aritmética de los valores pico y RMS no se aplica si las ondas se estiran fuera de fase, como en Figura 2. Sin embargo, si las ondas sinusoidales están exactamente en fase, como en imagen 3las ondas sinusoidales resultante y componente alcanzan sus valores máximos al mismo tiempo, y

[begin{matrix}{{E}_{m}}={{V}_{m1}}+{{V}_{m2}} & and & E={{V}_{T}}={{V}_{1}}+{{V}_{2}} end{matrix}]

Por lo tanto, el valor RMS es la suma de las ondas sinusoidales en fase en lugar de la suma de los valores RMS de las ondas individuales.

imagen 3 Sumar los valores instantáneos de dos sinusoides en fase

Representación de una onda sinusoidal mediante un diagrama de fase

Una vez que se supone que la suma de ondas sinusoidales de la misma frecuencia da como resultado una onda semilla de la misma frecuencia, es necesario realizar el tedioso procedimiento numeros 2 y 3 no está justificado. La información básica a partir de la cual construimos estos gráficos fue solo sus valores RMS y el ángulo de fase entre ellos. El valor RMS y el ángulo de fase también se utilizarán para identificar el resultado.

Si dibujamos fasores para los dos voltajes sinusoidales en el circuito de Figura 1, el fasor giratorio para el voltaje instantáneo a través del inductor siempre permanecerá exactamente p/2 radianes por delante del fasor giratorio para el voltaje instantáneo a través de la resistencia. Por lo tanto, estos reguladores de voltaje no se mueven entre sí.

Las ondas sinusoidales de la misma frecuencia pueden representarse mediante fasores "estáticos" y el ángulo entre los fasores es el mismo que el ángulo de fase entre las ondas sinusoidales.

Cuando dibujamos fasores para cantidades eléctricas, hacemos que la longitud de las fases sea proporcional al valor RMS del sineton que representan. Estas corrientes alternas pertenecen al dominio de la frecuencia, donde los ángulos generalmente se expresan en grados.

En el circuito una serie simple de Figura 1, la corriente es común a todos los componentes. Por lo tanto, en el diagrama fasorial para un circuito alterno en serie, como en Figura 4dibujamos un fasor que representa el valor RMS de la corriente a lo largo del eje de referencia del diagrama (apuntando hacia las tres en punto).

Dado que el voltaje a través de la resistencia es igual a la corriente que fluye a través de ella, el fasor V_R apunta en la misma dirección que el fasor de corriente. Dado que el voltaje a través del inductor envía una corriente a través de él a 90°, V_L 90° en sentido antihorario desde el eje de referencia.

Figura 4 Diagrama fasorial para el circuito de la Figura 1

el diagrama de fase de Figura 4 Es mucho más fácil de dibujar que los gráficos de voltaje instantáneo. Figura 2y muestra de un vistazo los valores RMS y los ángulos de fase.

Símbolos alfabéticos para cantidades de faser

Al estudiar el comportamiento de los circuitos eléctricos y magnéticos, se encuentran tres tipos cantidad.

Escalada

escalares son cantidades que tienen magnitud pero no dirección ni ángulo. La resistencia, la inductancia y la capacitancia son escalas. El voltaje y la corriente en los circuitos de CC son escalas, al igual que los valores instantáneos de voltaje y corriente en los circuitos de CA. Las escalas se indican mediante símbolos de letras en cursiva clara (p. ej. R, L, contra, V, yo, vy yo). Las cantidades escalares se pueden sumar mediante sumas algebraicas simples.

Vectores

Vectores son cantidades que tienen tanto magnitud como dirección. La fuerza electrostática, la intensidad del campo eléctrico y la densidad de flujo magnético son cantidades vectoriales.

Este artículo utiliza símbolos de letras en negrita y cursiva (p. ej. F, miy b( ) para representar cantidades vectoriales, y los mismos símbolos de letras en cursiva clara para representar cantidades vectoriales. Por ejemplotamaño del vector F es la cantidad escalar F.

La mayoría de las cantidades vectoriales eléctricas tienen tres dimensiones. Sin embargo, si todos los vectores en un cálculo dado se encuentran en el mismo plano, podemos tratarlos como bidimensionales. Debido a que los vectores son multidimensionales, la mayoría de las operaciones de álgebra vectorial, como la suma y la multiplicación, difieren significativamente de las operaciones aritméticas simples para escalas.

Graduado

Graduado son cantidades que tienen tanto magnitud como dirección. La notación fasorial es un método conveniente para representar ondas extendidas en circuitos de CA. Por ejemplo, un voltaje sinusoidal se puede representar como V =V∠ϕ, donde V es la magnitud RMS y ϕ es el ángulo de fase.

Usamos letras romanas en negrita para los phasers para distinguirlos de los vectores, que se muestran en cursiva y negrita. Al igual que con los vectores, la misma letra en cursiva clara indica el tamaño de un fasor.

Usando la notación fasorial, podemos reescribir ecuación 2 como

[begin{matrix}{{text{E}}_{text{T}}}text{=}{{text{V}}_{text{R}}}text{+}{{text{V}}_{text{L}}} & {} & left( 3 right) end{matrix}]

Interferencia de transeúntes por construcción geométrica

En un diagrama fasorial, la suma de dos cantidades fasoriales es la diagonal desde el origen hasta la esquina opuesta del paralelogramo con los dos fasores como lados.

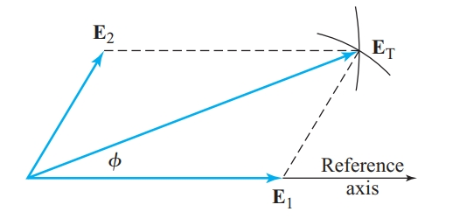
La resultante se puede tomar con una regla y un compás, como se muestra en Figura 5. Usando un radio igual a una longitud mi₁dibujar un arco con la parte superior de la mi₂ fáser como centro. Entonces, usando un radio igual a una longitud mi₂dibujar un arco con el punto mi₁ como sustituto. Luego dibujamos la resultante conectando el origen a la intersección de los dos arcos.

Figura 5 Una construcción geométrica de un fasor resultante.

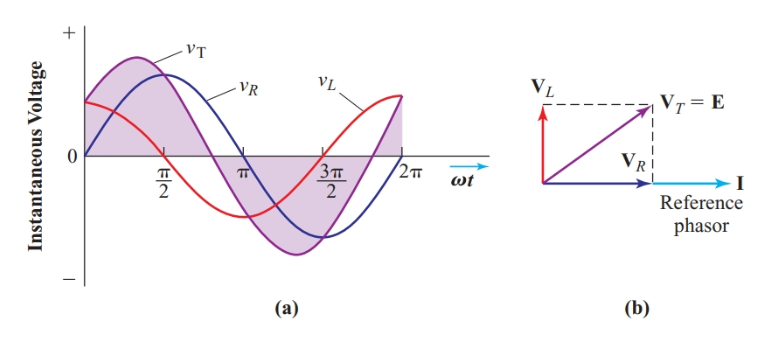
Aplicando esta técnica al circuito en serie de Figura 1 muestra cómo sus ángulos de amplitud y fase de mi, yo, V_Ry V_L conectado. Figura 6 compare el gráfico de seno y el diagrama de fase para esta serie de circuitos. Aunque podemos determinar valores RMS y ángulos de fase a partir de gráficos de seno i Figura 6(a)es mucho más fácil obtener esta información del diagrama fasorial de entrada Figura 6(b).

Figura 6 Gráfico sinusoidal y diagrama fasorial para el circuito de la Figura 1

Si dibujamos las resistencias con cuidado, podemos medir los voltajes rms y el ángulo de fase entre el voltaje aplicado mi y la corriente yo a exactamente dos dígitos. Aunque las soluciones gráficas no son lo suficientemente precisas para muchos problemas de circuitos de CA, podemos usar aproximaciones de un diagrama fasorial para verificar las respuestas calculadas.

Los diagramas de Prosper también nos ayudan a encontrar el signo correcto del seno, coseno o tangente para ángulos mayores de 90°.

Se agregaron escalones verticales

Anteriormente vimos que los valores RMS de las ondas sinusoidales en fase se pueden sumar aritméticamente. Por lo tanto, los transeúntes con el mismo ángulo de fase se pueden agregar simplemente. Del mismo modo, cuando el ángulo entre un par de fasores es exactamente 180°, la suma de los fasores es simplemente la diferencia de los dos fasores. Para dos fasores con un ángulo de exactamente 90° entre ellos, podemos usar la trigonometría para encontrar la suma de los fasores.

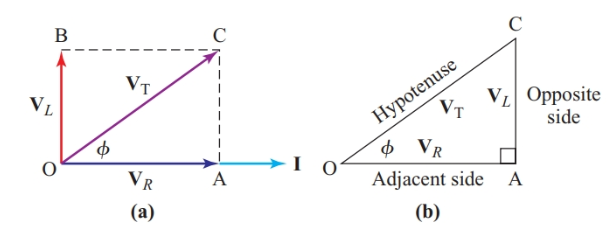
En el circuito una serie simple de Figura 1, la caída de voltaje a través de la resistencia está directamente en fase con la corriente, y el voltaje a través del inductor se adelanta a la corriente directamente en 90°. Por lo tanto, los dos fasores de tensión están desfasados ​​exactamente 90°. En la construcción geométrica de sus resultados i Figura 8(a)el paralelogramo se convierte en un rectángulo de lado AC exactamente igual al tamaño del V_L. Por lo tanto, el triángulo i Figura 8(b) muestra exactamente los mismos datos que el diagrama de fase clásico de Figura 8(a), que tienen todos los fásers desde el origen. Estos diagramas triangulares son útiles para analizar circuitos de CA que tienen tanto resistencia como reactancia.

Figura 8 Phasers de ángulo recto agregados

Como el triángulo OAC es un triángulo rectángulo,

[tan phi =frac{oppositetext{ side}}{adjacenttext{ side}}=frac{AC}{OA}=frac{{{V}_{L}}}{{{V}_{R}}}]

Dados los voltajes rms a través del inductor y la resistencia, el ángulo de fase ϕ se puede encontrar usando tablas trigonométricas o una calculadora con tan^-1 función.

[begin{matrix}phi ={{tan }^{-1}}frac{{{V}_{L}}}{{{V}_{R}}} & {} & left( 4 right) end{matrix}]

donde broncearse^-1 significa "el ángulo al que es tangente".

Ahora tenemos varios métodos para elegir para encontrar la magnitud del voltaje total, mi_j. trigonometría,

[sin phi =frac{oppositetext{ side}}{hypotenuse}=frac{AC}{OC}]

Por lo tanto,

[begin{matrix}{{E}_{T}}=frac{{{V}_{L}}}{sin phi } & {} & left( 5 right) end{matrix}]

Del mismo modo,

[cos phi =frac{text{adjacent side}}{hypotenuse}=frac{OA}{OC}]

Por lo tanto,

[begin{matrix}{{V}_{T}}=frac{{{V}_{R}}}{cos phi } & {} & left( 6 right) end{matrix}]

Otro método utiliza el teorema de Pitágoras, que establece que el cuadrado de la longitud de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de las longitudes de los otros dos lados. yo Figura 8(b),

[O{{C}^{2}}=O{{A}^{2}}+A{{C}^{2}}]

[begin{matrix}{{V}_{T}}=sqrt{V_{R}^{2}+V_{L}^{2}} & {} & left( 7 right) end{matrix}]

Tenga en cuenta que el componente de resistencia generalmente se cita antes que el componente reactivo i Ecuación 7. combinaciones Ecuaciones 7 y 4 dado

[begin{matrix}{{E}_{T}}=sqrt{V_{R}^{2}+V_{L}^{2}}angle {{tan }^{-1}}frac{{{V}_{L}}}{{{V}_{R}}} & {} & left( 8 right) end{matrix}]

Escala para expresar números complejos

Cuando describimos un fasor expresando su magnitud y el ángulo del fasor con respecto al eje de referencia, estamos usando coordenadas polares. Estas coordenadas especifican la posición de la punta del phaser en términos de distancia a lo largo de un radio desde el origen y el ángulo medido desde el eje de referencia.

Las coordenadas polares corresponden a las medidas que obtenemos con instrumentos como voltímetro, amperímetroy medidor de potencia.

Aplicando relaciones trigonométricas a un diagrama de fase de Figura 8, debemos determinar las coordenadas polares del voltaje total a partir de dos componentes verticales, uno de los cuales está ubicado a lo largo del eje de referencia. Podemos usar el mismo método para obtener Coordenadas rectangulares (o componentes verticales) de cualquier fasor en forma polar mi∠ϕ.

Como se muestra en el Figura 9componente del eje de referencia (o componente real(e) es la magnitud del fasor multiplicada por el coseno de su fasor. El componente del cuadrante (o componente imaginario) es la magnitud del fasor multiplicada por el seno de su ángulo de fase.

Figura 9 Determinar las coordenadas rectangulares de un fasor

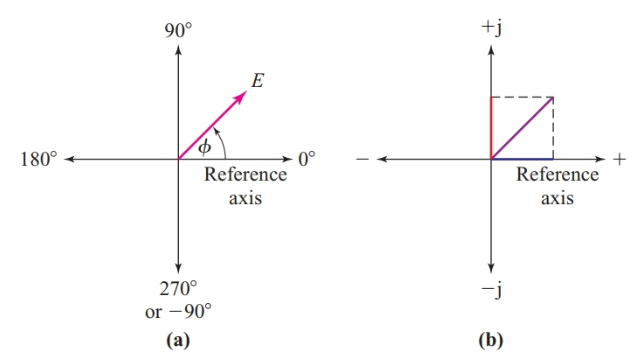
Las coordenadas rectangulares de un fasor representan la longitud de los ejes a lo largo de los ejes del plano complejo. Imagen 10 muestra cómo los ángulos en coordenadas polares corresponden a las cuatro direcciones posibles para las coordenadas en el plano complejo.

En el plano complejo, multiplicar un fasor por el operador j lo rota 90° en sentido antihorario. Para rotar el fasor 90° adicionales, simplemente multiplique el operador ja una y otra vez. Entonces multiplicando el fasor por j² la dirección cambia 180°.

En coordenadas polares, invertir la dirección de un fasor es equivalente a multiplicar por -1. Entonces j²=–1. Como $j=sqrt{-1}$ no tiene solución, los números precedidos por el operador +jo -j se llaman números imaginarios. Si un phaser se multiplica por j tres veces, gira un total de 270°. desde que soy³ = j² x j y j² = -1, el operador –j corresponde a una rotación de 270°.

Imagen 10 Direcciones correspondientes en (a) coordenadas polares y (b) coordenadas rectangulares

Las coordenadas rectangulares de un fasor son un número real (que puede ser positivo o negativo) y un número imaginario identificado por +j o –j. El componente real siempre aparece antes que el componente imaginario. La fórmula para convertir un fasor de voltaje de coordenadas polares a coordenadas rectangulares es

[begin{matrix}Eangle phi =+Ecos phi +jEsin phi & {} & left( 9 right) end{matrix}]

Resta de cantidades fasoriales

Cuando dos fasores se expresan en coordenadas rectangulares, uno se puede restar del otro simplemente restando los componentes reales (o eje de referencia) y luego los componentes imaginarios (o de cuadratura). Las coordenadas rectangulares resultantes se pueden convertir a forma polar.

Multiplicación y división de cantidades de faser

La multiplicación y división de cantidades de paso en forma polar es el más simple de los procesos algebraicos complejos.

Para multiplicar cantidades expresadas en forma polar, multiplica sus magnitudes y suma sus ángulos de paso algebraicamente.

[begin{matrix}{{E}_{1}}times {{E}_{2}}={{E}_{1}}angle {{phi }_{1}}times {{E}_{1}}angle {{phi }_{2}}={{E}_{1}}{{E}_{2}}angle {{phi }_{1}}+{{phi }_{2}} & {} & left( 10 right) end{matrix}]

Para dividir las cantidades de fasores expresadas en forma polar, divida sus magnitudes y reste algebraicamente sus ángulos de fase.

[begin{matrix}{{E}_{1}}div {{E}_{2}}={{E}_{1}}angle {{phi }_{1}}div {{E}_{1}}angle {{phi }_{2}}=frac{{{E}_{1}}}{{{E}_{2}}}angle {{phi }_{1}}-{{phi }_{2}} & {} & left( 11 right) end{matrix}]

Aunque el procedimiento para multiplicar y dividir cantidades fasoriales expresadas en coordenadas rectangulares es simple, requiere habilidad en el manejo de términos algebraicos. A menudo es más seguro multiplicar y dividir fasores por el método polar más simple.

Con una calculadora que tiene funciones de conversión de coordenadas, estas conversiones son la forma más rápida de hacer multiplicaciones y divisiones.

Resumen

• Una onda sinusoidal de la misma frecuencia es la suma de dos ondas sinusoidales de la misma frecuencia.

• El valor pico de la suma de dos ondas sinusoidales con la misma frecuencia no es igual a la suma de sus valores pico a menos que las ondas sinusoidales estén en fase.

• Las coordenadas polares de un fasor dan su magnitud y ángulo fasorial.

• Las coordenadas rectangulares de un fasor dan los valores de sus componentes reales e imaginarias.

• Los fasores se pueden sumar o restar de un diagrama de fasores.

• Los pasajes se pueden sumar o restar cuando se expresan en coordenadas rectangulares.

• Los pasajes son más fáciles de multiplicar o dividir cuando se expresan en coordenadas polares.