Los conductores transportan corriente eléctrica. Los aisladores protegen a los conductores y protegen a las personas de los conductores. Que un material sea conductor o aislante depende de sus átomos y de la relación de cada átomo con los átomos que lo rodean.
Los aisladores pueden fallar si están sujetos a voltajes excesivos. Asimismo, los conductores pueden destruirse si pasa demasiada corriente a través de ellos. Los mejores materiales conductores tienen la resistencia más baja, es decir, la resistencia por metro cúbico. Los mejores materiales aislantes tienen el voltaje de ruptura más alto para un espesor dado.
La resistencia de cualquier conductor se puede calcular a partir del conocimiento de su sección transversal, longitud y resistencia del material. Cuando se conoce la resistencia, se puede determinar la caída de voltaje a lo largo de un conductor y la potencia disipada en él para una corriente dada.
aisladores
La Figura 1 muestra algunos arreglos típicos de conductores y aisladores. Un cable eléctrico generalmente consta de alambre conductor de cobre rodeado por una cubierta aislante de goma o plástico. A veces hay más de un conductor y, por supuesto, estos están aislados individualmente.
Higo. 1: Conductores y aisladores
Los conductores utilizados para fines industriales y domésticos suelen tener hilos de cobre trenzados con aislamiento de caucho o plástico. En equipos electrónicos, los cables planos de alambre delgado y los conductores de placa de circuito delgado son ampliamente utilizados.
Incluso en los mejores materiales aislantes, hay electrones libres que fluyen entre los átomos. Por lo tanto, una corriente eléctrica muy pequeña puede fluir a través de un aislador. En circunstancias normales, esta corriente es tan pequeña que es insignificante. La corriente también puede fluir en la superficie de un aislador, especialmente si el aislamiento está sucio o mojado. Esto es particularmente notable cuando los cables aéreos de alta tensión tienen aisladores de porcelana durante una tormenta eléctrica, cuando se produce ondulación en la superficie del aislador.
Si se aplica una diferencia de potencial lo suficientemente alta a través de un aislador, los electrones pueden extraerse de los átomos y puede fluir una corriente sustancial. Esto se denomina ruptura del aislamiento y, por lo general, el aislamiento se destruye. Para ayudar a prevenir averías, todos los materiales aislantes están clasificados para el voltaje máximo que se puede aplicar de manera segura. La Tabla 1 enumera los voltajes de ruptura típicos (o resistencias dieléctricas) para varios materiales aislantes. Puede verse que el aire tiene el voltaje de ruptura más bajo, a 30 kV/cm, y la mica el más alto, a 2000 kV/cm.
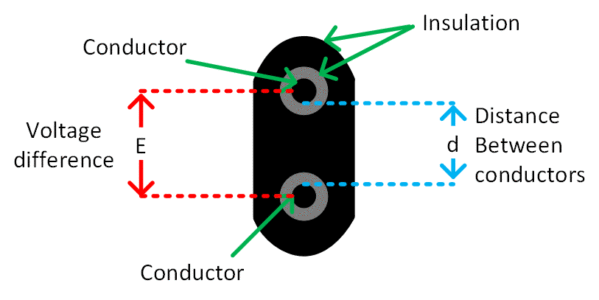
La fuerza del campo eléctrico es una medida de la tensión eléctrica acumulada en un aislador. La fuerza del campo siempre debe ser menor que la fuerza que podría causar la ruptura del aislamiento. La intensidad del campo es simplemente el voltaje aplicado dividido por el espesor del aislamiento.
$begin{matriz} text{intensidad del campo eléctrico,}xi text{=}frac{E}{d} & {} & left( 1 right) end{matriz}$
Donde E está en voltios y d está en metros, la unidad de intensidad de campo es volt/metro (V/m). El escenario se ilustra en la Figura 2 y se explora con más detalle en el siguiente ejemplo.
Tabla.1: Tensiones de ruptura típicas de algunos materiales aislantes
| Contenido | Tensión de ruptura (kV/cm) |
| Aire | 30 |
| porcelana | 70 |
| Goma | 270 |
| Vidrio | 1200 |
| Mica | 2000 |
Figura 2 (a): cable de dos conductores
Fig.2 (b): Sección del cable
Un ejemplo
Dos conductores eléctricos recubiertos de goma están separados por solo 0,25 cm.
(a). Calcular la fuerza del campo eléctrico en el aislamiento cuando la diferencia de potencial entre los conductores es de 25 V.
(b). Determine la diferencia de potencial mínima entre los conductores que pueden causar la ruptura del aislamiento.
La solución
De la ecuación (1)
$text{fuerza del campo eléctrico,}xitext{=}frac{E}{d}=frac{25}{0.25}=100 V/cm$
De la Tabla 1, la ruptura del aislamiento ocurre para el caucho a 270 kV/cm.
$Etext{=}dtimes text{breakdownvoltage=0}text{.25*270=67}text{.5kV}$
Conductores
La función de un conductor es conducir corriente de un punto a otro en un circuito eléctrico. Los cables eléctricos suelen estar hechos de conductores de cobre cubiertos con material aislante de caucho o plástico. Los cables que deben transportar grandes corrientes deben tener conductores relativamente gruesos. Cuando se trata de corrientes muy bajas, los conductores pueden ser tiras delgadas de cobre o incluso papel de aluminio. Entre estos dos extremos existe una amplia gama de conductores para diferentes aplicaciones. En la Figura 3 se muestran tres tipos diferentes de cables utilizados en equipos electrónicos. El identificado como cable coaxial tiene un conductor central aislado y una pantalla conductora trenzada circular, así como una cubierta aislante exterior. Los otros dos son cables multiconductores, uno circular y otro plano.
Fig.3: Diferentes tipos de cables
Muchos tipos diferentes de cables se utilizan con equipos electrónicos.
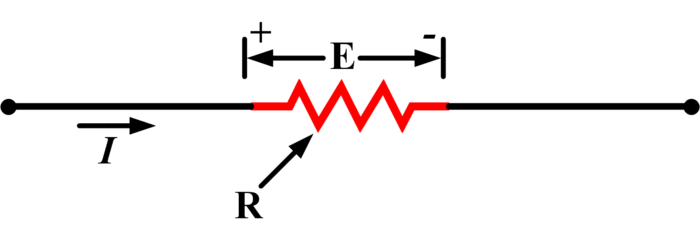
Dado que cada conductor tiene una resistencia finita, la caída de voltaje de un extremo del conductor al otro hace que fluya una corriente (Figura 4). Cuando los conductores son largos y/o transportan grandes corrientes, una caída en el voltaje del conductor puede resultar en un rendimiento insatisfactorio del equipo suministrado. poder (yo2R) también se disipa en todos los conductores que llevan corriente, lo que, por supuesto, es energía desperdiciada.
Figura 4 (a): El flujo de corriente a través de un conductor produce una caída de voltaje
Figura 4 (b): la resistencia del conductor provoca una caída de tensión
La resistencia de un conductor (R) se determina aplicando la ley de Ohm a la caída de tensión y al nivel de corriente. Luego se usa la resistencia por unidad de longitud (R/l) para seleccionar un calibre de cable apropiado.
En casos extremos, la potencia disipada en los conductores puede generar suficiente calor para destruir el aislamiento o incluso derretir el conductor. Cuando se conoce la resistencia por unidad de longitud del conductor, la caída de tensión del conductor y la disipación de potencia se calculan fácilmente.
Para seleccionar un conductor para una aplicación en particular, primero se determina su resistencia por unidad de longitud a partir del nivel de corriente y la caída de voltaje aceptable a lo largo del cable. Luego, la tabla se usa para encontrar un medidor de cable con la resistencia calculada por kilómetro (R/km) o el siguiente valor R/km más bajo.
Resistencia del conductor
La resistencia por unidad de longitud de un conductor dado no siempre está disponible. Por lo tanto, permita todas las combinaciones posibles de longitud y sección transversal del cable. Se utiliza la resistencia específica del material conductor.
La resistencia específica (o resistividad) de un material es la resistencia de 1 metro cúbico del material.
Por supuesto, dado que algunos metales son mejores conductores que otros, cada uno tiene su propia resistencia específica. La Tabla 2 enumera las resistividades específicas de los metales de las vetas.
El símbolo utilizado para la resistencia específica es ρ (letra griega minúscula rho), y las unidades de p son ohmímetros (Ωm).
Considere el metro cúbico de cobre que se muestra en la figura 5(a). De la Tabla 2, la resistencia específica del cobre es p = 1.72 X 10-8 Ohm.
Fig.5: Bloque de resistencias
Si un cubo de cobre de 1 metro tiene una resistencia de ρ Ω, tres cubos en serie tendrán una resistencia de 3 ρ Ω y dos en paralelo tendrán una resistencia de ρ/2 Ω.
Si la longitud del cobre se duplica o triplica colocando bloques uno al lado del otro como se muestra en la Figura 5(b), la resistencia aumenta. (Se dice que los bloques u otros componentes conectados entre sí de esta manera están conectados en serie. 2p Ω es la resistencia de dos bloques conectados en serie y la resistencia de tres es 3p Ω, y así sucesivamente. De esto podemos deducir la resistencia total de cualquier longitud de cobre con una sección transversal de 1 m2 sí,
$begin{align} & R=rho times (text{longitud en metros) & =1,72*{{10}^{-8}}times (text{longitud en metros) } Omega fin{alinear}$
Ahora considere el efecto de duplicar la sección transversal del cobre colocando dos bloques como se muestra en la Figura 5(c). (Se dice que los bloques u otros componentes conectados entre sí de esta manera están conectados en paralelo. A medida que se duplica la sección transversal, la resistencia se reduce a la mitad. Si se conectan cuatro bloques en paralelo. [Figure 5 (d)] la resistencia se rompe. Para bloques conectados en paralelo, la resistencia se puede escribir como,
[R=frac{rho }{text{cross-sectional area in }{{text{m}}^{text{2}}}}]
Tabla.2: Resistencia específica para metales eléctricamente conductores
| Metal | Resistencia específica a 20 deC (Ωm) |
| De dinero | 1,64*10-8 |
| Cobre | 1,72*10-8 |
| Oro | 2,45*10-8 |
| Aluminio | 2,83*10-8 |
| Tungsteno | 5,5*10-8 |
| níquel | 7,8*10-8 |
Cuando los bloques se colocan en serie y en paralelo [Figure 5(e)]las dos ecuaciones anteriores se combinan para dar
[begin{matrix} R=rho frac{l}{a} & {} & left( 2 right) end{matrix}]
Donde R es la resistencia en ohmios, p es la resistencia específica del material, l es la longitud en metros y a es la sección transversal im2.
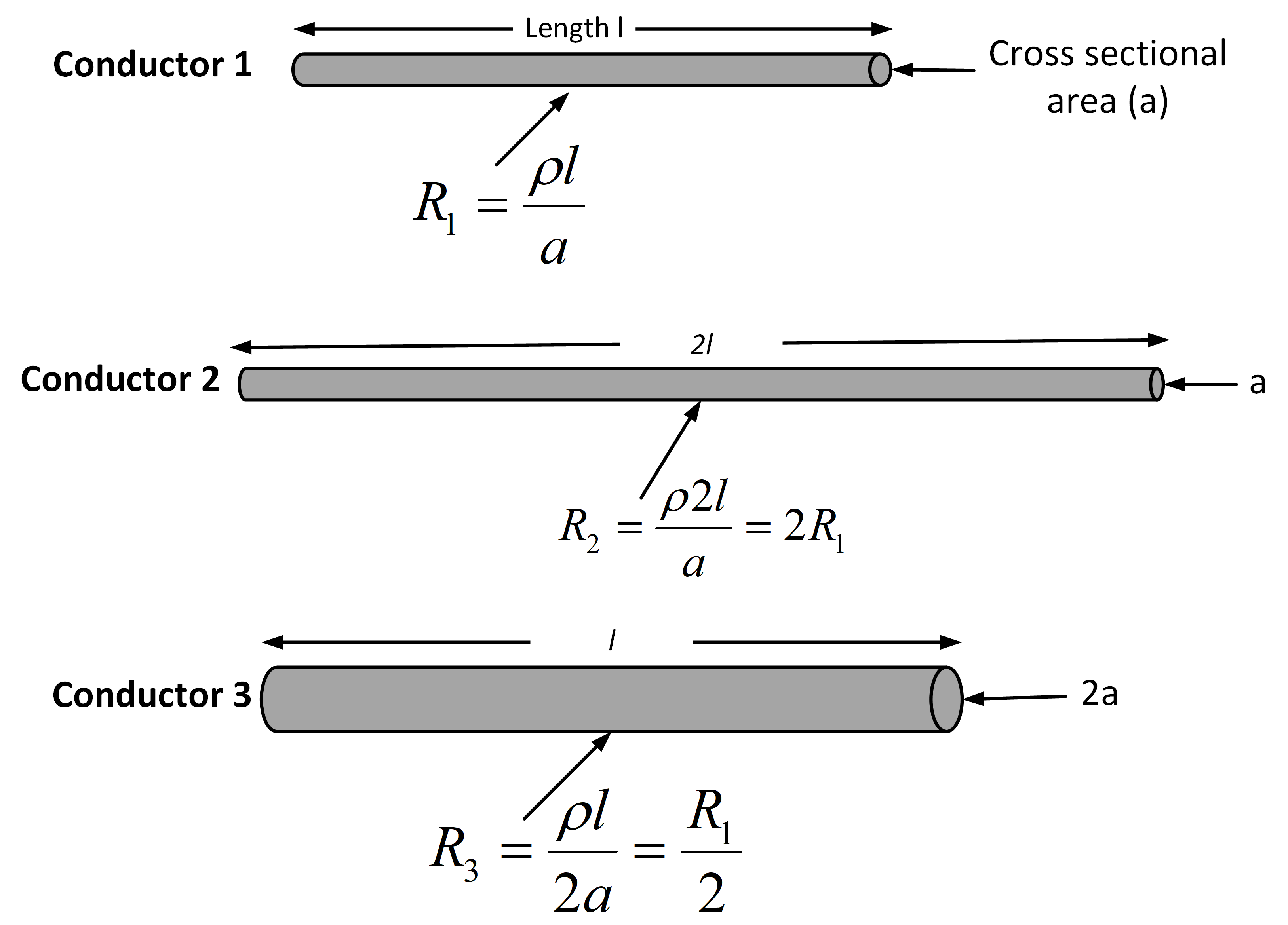
En la figura 6 se muestran conductores cilíndricos de varios tamaños. Se ve que la resistencia de un conductor de longitud l1 y sección transversal a1 se calcula como
[{{R}_{1}}=rho frac{{{l}_{1}}}{{{a}_{1}}}]
Fig.6: Resistencia del conductor a diferentes longitudes
La resistencia de un conductor está determinada por la longitud, la sección transversal y la resistencia específica del material conductor.
Un conductor similar con la misma sección transversal y el doble de largo tiene una resistencia de 2R1. Además, un conductor de igual longitud que el primero pero con una sección transversal de 2a tiene una resistencia R1/2.
La resistencia de cualquier longitud de conductor de cualquier sección transversal se puede calcular a partir de la ecuación (2). Una vez que se conocen R, l y a, la ecuación se puede reescribir para determinar la resistencia específica:
Un ejemplo
Determine la resistencia de 20 m de alambre de cobre recocido de 2 mm de diámetro.
La solución
Área de la sección transversal:
[a=frac{pi {{D}^{2}}}{4}=frac{pi {{left( 2times {{10}^{-3}} right)}^{2}}}{4}=pi times {{10}^{-6}}{{m}^{2}}]
De la ecuación (2)
[R=rho frac{l}{a}]
De la Tabla 2, para cobre
$rho =1.72*{{10}^{-8}}$
Por lo tanto,
[R=1.72times {{10}^{-8}}times frac{20}{pi times {{10}^{-6}}}=0.109Omega ]
La resistencia de cualquier conductor se puede calcular a partir del conocimiento de su sección transversal, longitud y resistencia del material. Cuando se conoce la resistencia, se puede determinar la caída de voltaje a lo largo de un conductor y la potencia disipada en él para una corriente dada.
Efectos de la temperatura en los conductores
Los valores de resistencia específicos dados en la Tabla 2 se refieren solo a materiales conductores a una temperatura de 20deC. Por lo tanto, en todos los cálculos de resistencia que utilizan la resistencia específica, se supone que la temperatura del conductor permanece constante en 20deC. Dado que la resistencia de los metales cambia con la temperatura, es necesario poder calcular los valores de resistencia a niveles de temperatura más altos o más bajos.
La resistencia de todos los metales puros tiende a aumentar a medida que aumenta la temperatura del metal. Esto puede explicarse por el hecho de que los átomos en realidad vibran a altas temperaturas y, por lo tanto, se convierten en más obstáculos en el camino de los electrones en movimiento. Debido a que la resistencia aumenta con el aumento de la temperatura, se dice que los metales tienen un coeficiente de temperatura positivo (PTC). Algunos materiales, especialmente los semiconductores, muestran una disminución de la resistencia cuando aumenta su temperatura. Estos tienen un coeficiente de temperatura negativo (NTC). En el rango de temperatura de operación normal, todos los metales exhiben una relación casi lineal entre resistencia y temperatura.
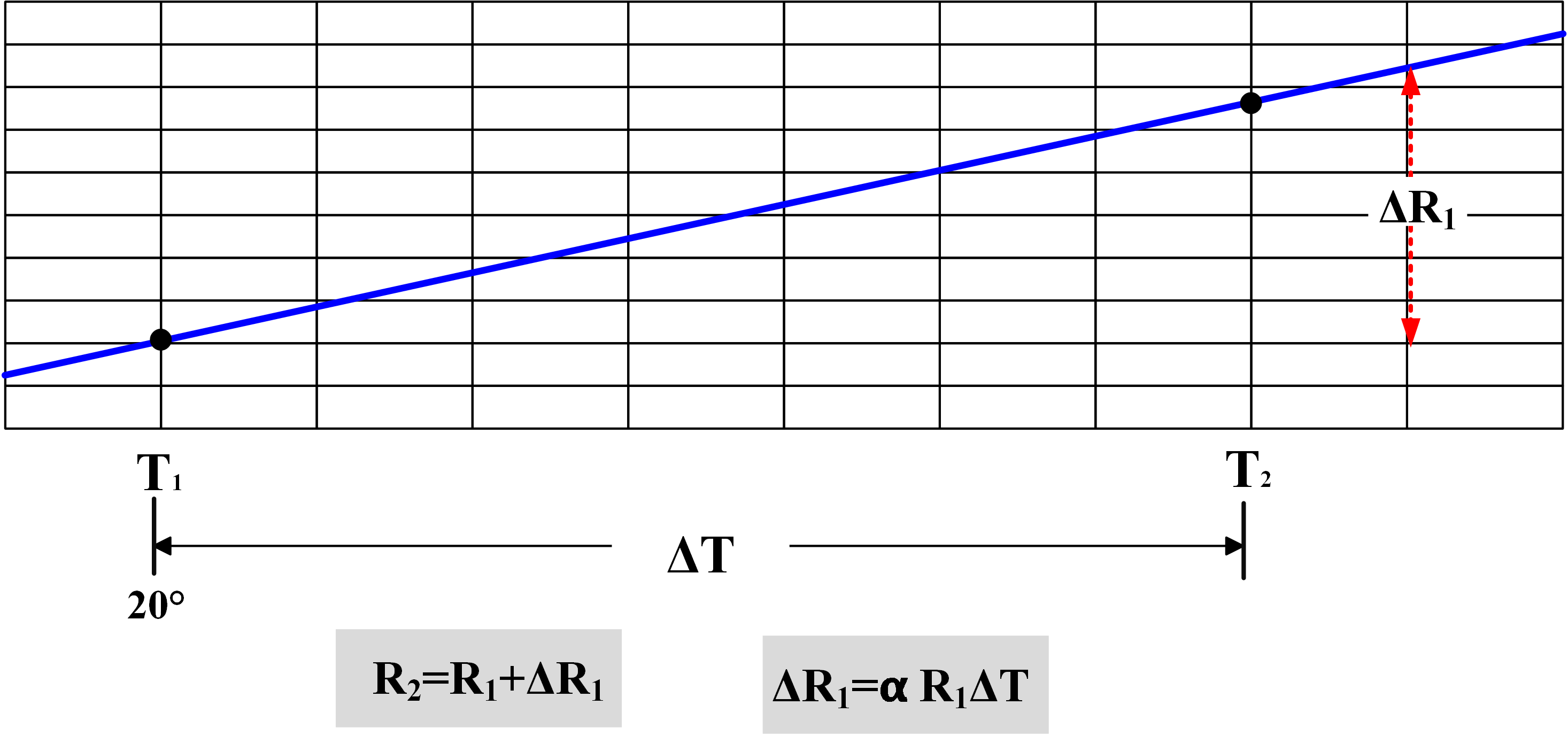
En la Figura 7(a), el cambio en la resistencia del cobre se representa en función de la temperatura. Tenga en cuenta que la resistencia del cobre parece llegar a cero a una temperatura de -234,5deC. El gráfico real no es tan completamente lineal como se muestra, sin embargo, la línea recta que pasa por -234.5deC es una proyección de la parte lineal del gráfico. Si la resistencia R1 a una temperatura de 20deC se conoce, se puede calcular el nuevo valor de resistencia a cualquier otra temperatura.
Figura 7(a): resistencia del cobre representada frente a la temperatura
Supongamos que R1 de 1 Ω a 20deC. Si la temperatura se reduce a -234,5deC, es el cambio de temperatura
[Delta T={{20}^{o}}C-left( -{{234.5}^{o}}C right)={{254.5}^{o}}C]
Y es el cambio en la resistencia contra el cambio de paso en la temperatura
[frac{Delta {{R}_{1}}}{Delta T}=frac{1}{254.5}=0.00393{Omega }/{^{o}C};]
si r1 20 tenía 10 Ω (en lugar de 1 Ω).deC, sería el cambio de resistencia con la temperatura
[frac{Delta {{R}_{1}}}{Delta T}=frac{10}{254.5}=0.0393{Omega }/{^{o}C};]
La cantidad 0.00393 Ω/deC es el coeficiente de temperatura del cobre a 20decontra
El símbolo α o (letra griega alfa minúscula) se utiliza para el coeficiente de temperatura. La Tabla 3 enumera los coeficientes de temperatura para varios metales a 20deC. Tenga en cuenta que la aleación de constantán tiene un coeficiente de temperatura extremadamente bajo. Esta característica hace que la constante sea útil en aplicaciones donde la resistencia debe permanecer lo más constante posible cuando cambia la temperatura. Los coeficientes de temperatura también se pueden determinar a temperaturas distintas de 20deC. La columna 3 de la Tabla 3 enumera los coeficientes de temperatura en 0decontra
Tabla.3: Coeficientes de temperatura para metales
| Contenido | debe ser 20decontra | 0 debedecontra |
| De dinero | 0.003 8 | 0.004 12 |
| Cobre | 0.003 93 | 0.004 26 |
| Oro | 0.003 4 | 0.004 65 |
| Aluminio | 0.003 9 | 0.004 24 |
| Tungsteno | 0.004 5 | 0.004 95 |
| níquel | 0.006 | |
| Constantino | 0.000 008 |
Higo. 7(b): Resistencia (R2) a una nueva temperatura (T2) a determinar a partir del conocimiento de R1 y T1 y el coeficiente de temperatura α
Como se explicó, para cualquier material conductor con resistencia R1,
[frac{Delta {{R}_{1}}}{Delta T}=alpha {{R}_{1}}]
O
$begin{matriz} Delta {{R}_{1}}=alpha {{R}_{1}}Delta Ttext{ } & cdots & [text{ see Figure 7 (a) and (b) }] end{matriz}$
y la resistencia R2 a una nueva temperatura T2 sí
$begin{matriz} {{R}_{2}}={{R}_{1}}+Delta {{R}_{1}}={{R}_{1}}+alfa {{R}_{1}}Delta Ttexto{ } & {} & [text{ see Figure 7 (b) }] end{matriz}$
Por lo tanto,
$begin{matriz} {{R}_{2}}={{R}_{1}}left( 1+alpha Delta T right) & {} & left( 3 right) end{matriz}$
¿Dónde estará R?1 La resistencia es de 20deC, α es el coeficiente de temperatura del material y ∆T es el cambio de temperatura de 20decontra
si r1 y R2 conocido, la ecuación (3) se puede reorganizar para determinar ∆T o α:
[Delta T=frac{1}{alpha }left( frac{{{R}_{2}}}{{{R}_{1}}}-1 right)]
[alpha =frac{1}{Delta T}left( frac{{{R}_{2}}}{{{R}_{1}}}-1 right)]
El coeficiente de temperatura en 0deC también se puede usar en la ecuación (3) si la resistencia es R1 medido en 0deC y ∆T es el aumento de temperatura 0decontra






¡Más Contenido!