conexión delta
En una conexión Delta, los lados de fase están conectados en un arreglo cíclico para formar un circuito cerrado como se muestra en la Figura 1. En cuanto a las corrientes de línea y de fase, están relacionadas entre sí como:
${{text{I}}_{text{línea}}}text{=}sqrt{text{3}}{{text{I}}_{text{fase}}}$
Lo que significa que tendremos un trozo de cable por ${}^{1}/{}_{sqrt{3}}$ multiplicado por una corriente de línea, sea cual sea la corriente de suministro que tengamos. Cuando está en conexión Delta, los voltajes de línea son iguales en fase:
${{text{V}}_{text{fase}}}text{=}{{text{V}}_{text{línea}}}$
En la Figura 1 se muestra una carga conectada en delta balanceada (con impedancias en fase).
Fig.1: Carga conectada en delta
Una ventaja de una carga conectada en delta sobre una carga conectada en Y es que las cargas se pueden agregar o quitar fácilmente en una fase de un triángulo ya que las cargas están conectadas directamente a través de las líneas. Además, para una potencia dada entregada a la carga, las corrientes de fase delta son más bajas que las de Y. Por otro lado, las tensiones de fase en triángulo son más altas que las de la conexión Y. Las fuentes rara vez se conectan en triángulo si las tensiones son no está perfectamente equilibrado, habrá un voltaje neto y, por lo tanto, una corriente que fluirá alrededor del triángulo. Por supuesto, esto provoca efectos de calor indeseables en la maquinaria generadora. Además, los voltajes de fase son más bajos en el generador conectado en Y, por lo que se necesita menos aislamiento. Los sistemas con cargas conectadas en triángulo son, por supuesto, sistemas de tres hilos, ya que no hay conexión neutra.
- También puedes leer: Conexión estrella trifásica (Y): alimentación trifásica, tensión, corriente
conexión delta Tensiones de línea y de fase
De la Figura 1, vemos que para una carga conectada en triángulo, los voltajes de línea son los mismos que los voltajes de fase. Por lo tanto, si los voltajes de línea están dados por
$begin{matriz} begin{alineación} & {{V}_{ab}}={{V}_{L}}angle {{30}^{o}} & {{V}_ {bc}}={{V}_{L}}ángulo -{{90}^{o}} & {{V}_{ca}}={{V}_{L}}ángulo -{{210}^{o}} final{alinear} & cdots & (1) final{matriz}$
Luego están los voltajes de fase.
Tensiones de línea y de fase para conexión en triángulo
Dónde
$begin{matriz} {{V}_{L}}={{V}_{p}} & cdots & (3) end{matriz}$
conexión delta Corrientes de línea y de fase
Si Zp=|Zp|∠θ , entonces las corrientes de paso son
Corrientes de fase en la conexión delta
Dónde
$begin{matriz} {{I}_{p}}=frac{{{V}_{L}}}{left| {{Z}_{p}} right|} & cdots & (5) end{matriz}$
La corriente en la línea aA es a través de KCL
${{I}_{aA}}={{I}_{AB}}-{{I}_{CA}}$
que después de simplificado
${{I}_{aA}}=sqrt{3}{{I}_{p}}ángulo -theta $
Las corrientes son la otra línea, obtenida de manera similar
${{I}_{bB}}=sqrt{3}{{I}_{p}}ángulo -{{120}^{o}}-theta $
${{I}_{cC}}=sqrt{3}{{I}_{p}}angle -{{240}^{o}}-theta $
La relación entre la amplitud de la corriente de línea y la fase es evidente en el caso delta.
$begin{matriz} {{I}_{L}}=sqrt{3}{{I}_{p}} & cdots & (6) end{matriz}$
Y las corrientes de línea son así.
Corrientes de línea en una conexión delta
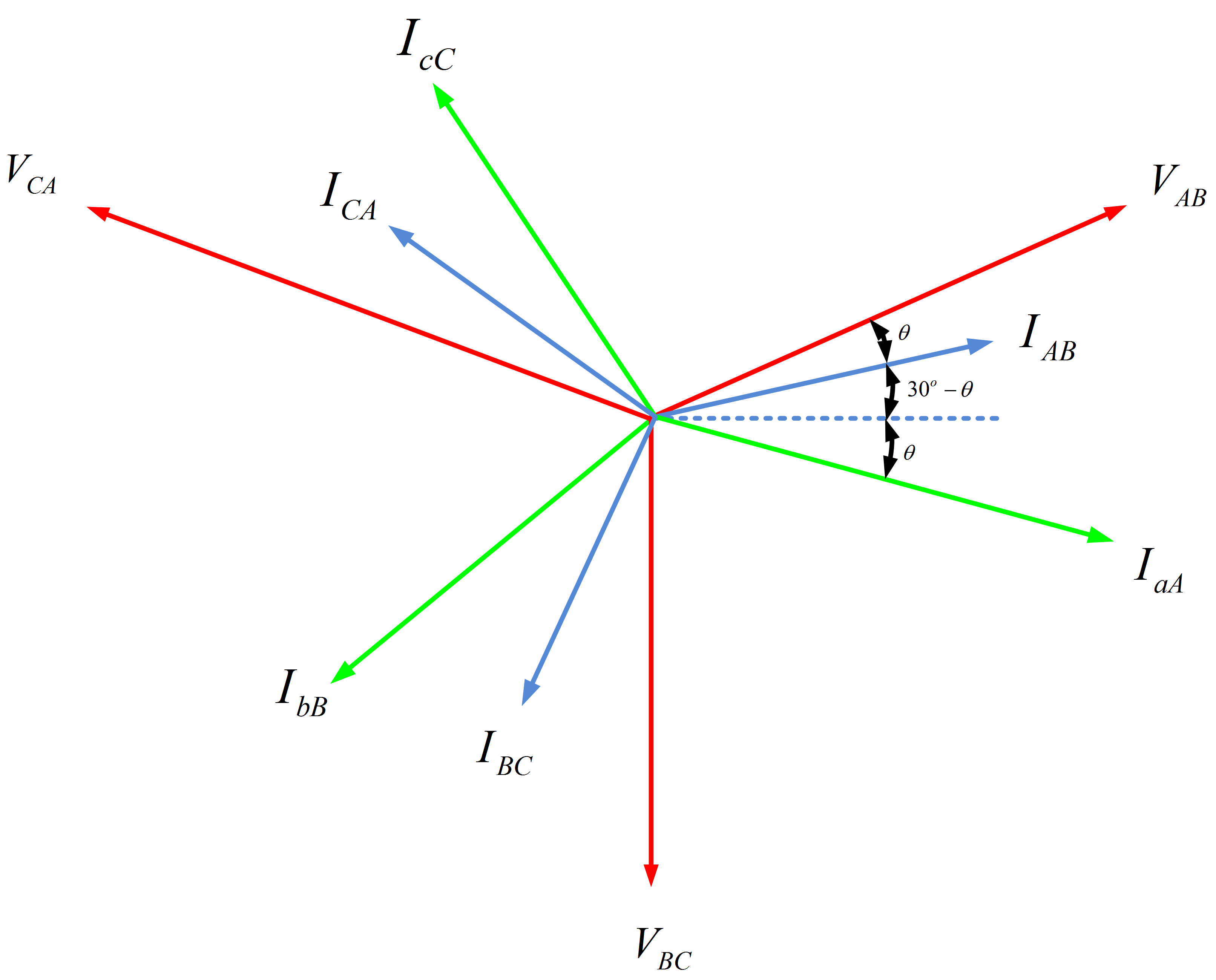
Entonces, las corrientes y los voltajes son conjuntos balanceados, como se esperaba. Las relaciones entre las corrientes de línea y de fase para la carga conectada en delta se resumen en el diagrama de fase de la Figura 2.
Fig.2: Diagrama fasorial para carga conectada en delta
conexión delta Fuente de alimentación trifásica
Ahora, obtengamos una fórmula para la potencia entregada a una carga trifásica balanceada con un ángulo de factor de potencia θ. Ya sea que la carga esté conectada en Y o en delta, debemos
$P=3{{P}_{p}}=3{{V}_{p}}{{I}_{p}}cos theta $
En el caso de Y,
$begin{align} & {{V}_{p}}={}^{{V}_{L}}}/{}_{sqrt{3}} & y &{ { I}_{p}}={{I}_{L}} fin{alinear}$
Y en el caso delta conectado,
$begin{align} & {{I}_{p}}={}^{{{I}_{L}}}/{}_{sqrt{3}} & y &{ {V}_{p}}={{V}_{L}} fin{alinear}$
En ambos casos, por tanto,
$P=3frac{{{V}_{L}}{{I}_{L}}}{sqrt{3}}cos theta $
O
Fuente de alimentación trifásica
Resumen
yo Caso conectado delta, tenemos la siguiente relación para corriente y voltaje:
$begin{align} & {{I}_{p}}={}^{{{I}_{L}}}/{}_{sqrt{3}} & y &{ {V}_{p}}={{V}_{L}} fin{alinear}$
yo Caja conectada en Y,
$begin{align} & {{V}_{p}}={}^{{V}_{L}}}/{}_{sqrt{3}} & y &{ { I}_{p}}={{I}_{L}} fin{alinear}$
Aunque el la fórmula para calcular la potencia sigue siendo la misma en ambos casos Cuál
$P=sqrt{3}{{V}_{L}}{{I}_{L}}cos theta $

¡Más Contenido!