Circuitos inductores de CA

En un circuito de CA, el voltaje aplicado cambia continuamente y la polaridad se invierte. Cualquier inductancia en el circuito generará una EMF inversa, que se opondrá al voltaje de la fuente.

Este fenómeno se puede observar configurando el experimento. Conecte una lámpara a una fuente de CC de seis voltios. Fíjate en su brillo. Ahora conecte la luz a un tomacorriente de seis voltios. transformador de ca, y observe el brillo. ¿Es más claro o más oscuro? La inductancia tiene un efecto indirecto sobre la corriente.

La resistencia a la corriente alterna debido a la inductancia o la capacitancia se llama reactancia. X es el símbolo alfabético de reactividad. Cuando la reactancia es causada por un inductor, se llama reactancia inductiva. La reactancia inductiva se mide en ohmios y se simboliza con una X_L.

Corriente y voltaje inducidos

Recuerde que el voltaje transmitido en una bobina es la fuerza contraelectromotriz. Contra fem contra la fuente. Por lo tanto, está desfasado 180 grados con respecto al voltaje de la fuente. Esta fuerza contraelectromotriz se opone al cambio, y la mayor fuerza contraelectromotriz se induce cuando el cambio de corriente es mayor.

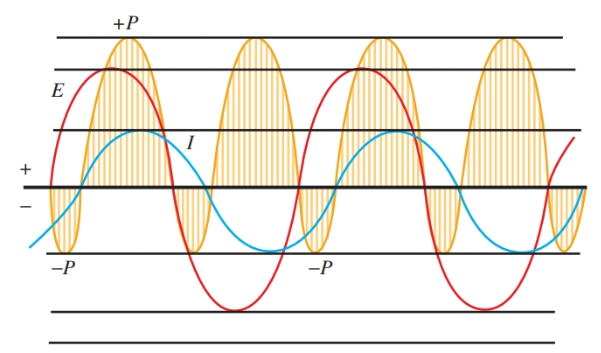
Estudiar Figura 1. La tasa de cambio actual es superior a 90 grados y 270 grados. En estos puntos, el voltaje aplicado debe ser máximo. La tensión de excitación también es máxima.

En 180 grados y 360 grados, hay pocos cambios en este momento. La corriente está en su valor máximo, lista para comenzar a disminuir. Como puede ver en la Figura 1, en un circuito con un inductor puro, la corriente está desfasada 90 grados con respecto al voltaje aplicado. La corriente reduce el voltaje.

Figura 1. Comparación de fem, fem y corriente. La fem contraria más grande ocurre cuando la corriente cambia a la velocidad más rápida.

Reactancia inductiva o impedancia inductiva

La cantidad de fuerza reactiva que se opone al flujo de corriente alterna se mide en ohmios. Se puede expresar matemáticamente de la siguiente manera:

${{X}_{L}}=2pi fL$

donde esta x_L es igual a la reactancia inductiva (impedancia inductiva) en ohmios, f es igual a la frecuencia en hercios, L es igual a la inductancia en henrys y π es aproximadamente 3,1416. Recuerde que a medida que aumenta la frecuencia o la inductancia, aumenta la reactancia inductiva. Están en proporción directa.

Un inductor en un circuito se comporta de manera diferente cuando se aplican diferentes señales de frecuencia, Figura 2. Un inductor de ocho Henry conectado a una señal de CC (f = 0) tiene una reactancia cero. Esto significa que el inductor de ocho Henry no bloquea la señal continua en absoluto.

Con la fórmula XL = 2πfL, se puede calcular la reactancia para frecuencias de 50, 100, 500 y 1000 Hz. Un gráfico parcial de los resultados muestra el aumento lineal de la reactancia a medida que aumenta la frecuencia.

Figura 2. A medida que aumenta la frecuencia, aumenta la reactancia inductiva.

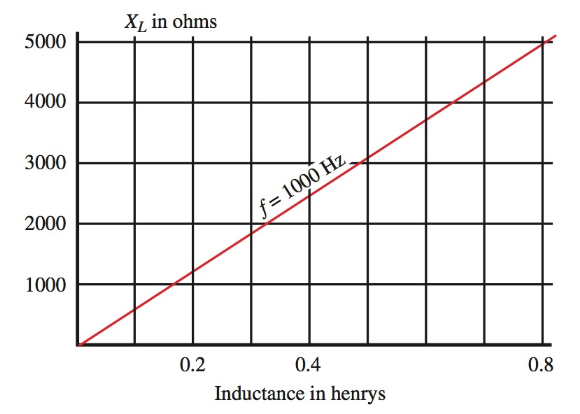
yo imagen 3, la frecuencia se mantuvo constante a 1000 Hz. La reactancia se grafica a medida que la inductancia aumenta de 0 henrys a 0,8 henrys. Tenga en cuenta el aumento lineal de la reactancia a medida que aumenta la inductancia.

Estos principios se pueden aplicar a filtrado y circuitos de acoplamiento. Sin embargo, primero debe comprender las características de la reactancia y cómo cambian con la inductancia y la frecuencia del voltaje aplicado.

Imagen 3. A medida que aumenta la inductancia, también aumenta la reactancia inductiva.

Potencia en circuitos inductivos

Poder real: La potencia consumida en un circuito resistivo es el producto del voltaje y la corriente: P = I × E. Esta es la potencia real consumida por un circuito. Está dado poder realy se da en unidades de vatios.

Poder reactivo: Sin embargo, en un circuito de CA con solo un inductor, esta fórmula no es cierta. En este tipo de circuito fluirá una corriente relacionada con la reactancia del circuito. La energía utilizada para crear el campo magnético se envía de regreso a la fuente cuando el campo colapsa. Esto es Poder reactivo. La potencia reactiva se mide en VAR, que significa Volt-Amp-Reactive.

Poder aparente: La combinación de potencia real y potencia reactiva da como resultado una medición de potencia que parece ser entregada a una carga. Esta potencia se llama potencia aparente. Es igual al producto de la tensión rms por la corriente rms. La potencia aparente se mide en VA o voltamperímetro.

[ApparentPower={{E}_{ff}}times {{I}_{ff}}]

Ejemplo de cálculo de potencia aparente

A 100E_destruir es un voltaje aplicado a algún circuito inductivo. causo_destruir de 10 amperios. La potencia aparente es:

Potencia aparente = 100 V × 10 A = 1000 VA Recuerde que los vatios no se utilizan para la potencia aparente.

Definición y fórmula del factor de potencia

La relación entre la potencia real y la potencia aparente en un circuito de CA se denomina factor de potencia (PF). No hay unidad. Se puede calcular usando trigonometría.

El factor de potencia es igual al coseno de la diferencia de fase entre la corriente y el voltaje. La fórmula está escrita:

[Powertext{ }Factor=cos theta =frac{Truetext{ }Power}{Apparenttext{ }Power}]

donde θ es el cambio de fase. Tenga en cuenta que al reorganizar esta fórmula, llegamos a la fórmula del poder real.

[begin{align}  & Truetext{ }Power=Apparenttext{ }Powertimes cos theta   & Truetext{ }Power={{E}_{ff}}times {{I}_{ff}}times cos theta  end{align}]

Por ejemplo, suponiendo que nuestro circuito anterior es puramente inductivo, determine el factor de potencia y el cambio de fase.

[PF=cos theta =frac{0W}{1000VA}=0]

El factor de potencia es 0. El ángulo cuyo coseno es 0 es de 90 grados, lo que nos dice que la corriente y el voltaje en un solo circuito inductivo están desfasados ​​90 grados, Figura 4.

Figura 4. Un circuito que es solo un inductor. La potencia real es cero y el voltaje es débil en 90 grados con respecto a la corriente.

Resistencia e inductancia en un circuito de CA

Si solo hay resistencia en un circuito de CA, la corriente y el voltaje están en fase, Figura 5. La potencia consumida es igual a I × E.

Incluso si la polaridad del voltaje cambia y la corriente se invierte, se consume potencia positiva. Una resistencia consume la misma cantidad de energía independientemente de la dirección en la que fluya la corriente. El factor de potencia en este tipo de circuito es igual a uno. La potencia aparente es igual a la potencia real.

Las características del circuito cambian cuando se coloca un inductor en serie con la resistencia. El componente no necesita ser un componente resistivo. El cable del que se enrolla la bobina tendrá cierta resistencia.

Figura 5. En un solo circuito resistivo, la potencia real y la potencia aparente son las mismas. La corriente y el voltaje están en fase.

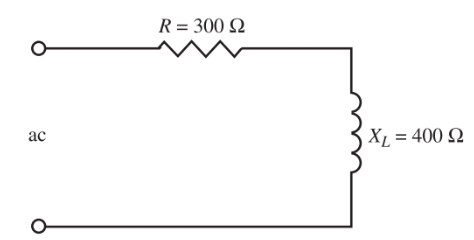
Referirse a Figura 6. La resistencia en serie es de 300 ohmios. La reactancia inductiva es igual a 400 ohmios. Este componente reactivo hará que la corriente se mueva en un ángulo de 90 grados o menos. Las fuerzas aguas arriba se pueden considerar como resistencia y reactancia.

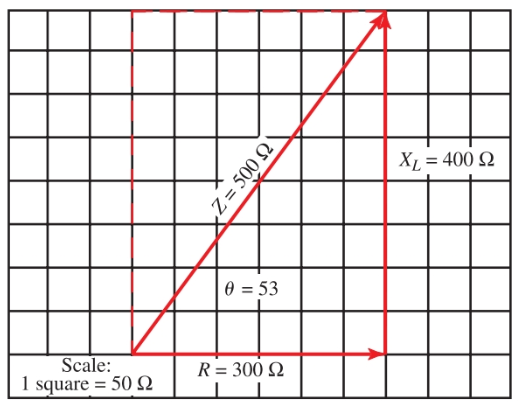
La resistencia y la reactancia están desfasadas 90 grados. Para encontrar la oposición final, la combinación de resistencia y reactancia, sume los vectores de las dos fuerzas. Referirse a Imagen 7.

Figura 6 . Un circuito RL que tiene una resistencia en serie de 300 ohmios y una reactancia inductiva de 400 ohmios.

Imagen 7. Suma de vectores X_L y R, que está desfasado 90 grados.

Se pueden agregar vectores al gráfico. Coloque la cola de la X_L vector en la punta de flecha del vector R. Luego, dibuje un vector desde el punto inicial del vector de resistencia hasta el final del vector de reacción, X_L. Este nuevo vector muestra la magnitud y la dirección de las fuerzas combinadas. θ es el ángulo entre este nuevo vector y el vector de resistencia, consulte la Figura 7.

Definición y fórmula de impedancia

La corriente alterna opuesta en un circuito que tiene resistencia y reactancia (el nuevo vector que creaste) es una resistencia. Z es el símbolo de la impedancia y se mide en ohmios.

Los problemas de impedancia generalmente se resuelven usando el teorema de Pitágoras. El teorema de Pitágoras establece que la hipotenusa de un triángulo rectángulo es igual a la raíz cuadrada de la suma de los cuadrados de los dos lados. Comúnmente se escribe:

$c=raíz cuadrada{{{a}^{2}}+{{b}^{2}}}$

Donde c es la hipotenusa y a y b son los otros dos lados del triángulo rectángulo.

En el problema de las Figuras 6 y 7, XL es 400 y R es 300. Encuentra la impedancia, Z.

$Z=sqrt{{{R}^{2}}+X_{L}^{2}}=sqrt{{{300}^{2}}+{{400}^{2}}}= 500Omega$

La impedancia del circuito es de 500 ohmios. El ángulo entre el vector Z y el vector R se llama ángulo de fase (θ) y muestra el cambio de fase entre la corriente y el voltaje como resultado de la componente reactiva. Por tanto, dado que cosθ es igual al factor de potencia:

[cos theta =frac{R}{Z}=frac{300}{500}=0.6]

El coseno de θ es igual a 0,6, el ángulo es 0,6 (alrededor de 53,1°) y el ángulo de fase es 0,6 (alrededor de 53,1°). Por lo tanto, la corriente se atrasa con respecto al voltaje en un ángulo de 53,1 grados.

Ahora se puede calcular la potencia real en este circuito. La potencia real en este circuito es igual a la potencia aparente multiplicada por el factor de potencia o cosθ.

$begin{align} & Truetext{ }Potencia=Aparentetext{ }Potenciaveces costheta & cos theta =frac{Verdaderotext{ }Potencia}{Aparentetext{ } Potencia } fin{alinear}$

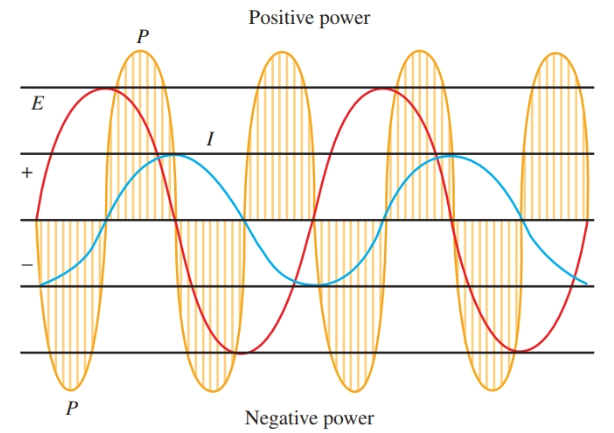
Las formas de onda se dibujan para corriente, voltaje y potencia. Imagen 8. Suponiendo un voltaje de CA aplicado de 100 V, la corriente en el circuito será igual a:

[I=frac{E}{Z}=frac{100V}{500Omega }=0.2A]

La potencia aparente es:

$Aparentetext{ }Potencia=Etimes I=100times 0.2A=20VA$

El verdadero poder es:

$Verdaderotext{ }Potencia=Eveces Iveces cos theta =100Vveces 0.2Aveces .6=12W$

Imagen 8. La relación entre voltaje, corriente y potencia en el circuito descrito en el texto.

Estos números se pueden verificar insertándolos en la fórmula del factor de potencia.

[PF=cos theta =frac{Truetext{ }Power}{Apparenttext{ }Power}=frac{12W}{20VA}=0.6]

No solo en la teoría sino en la práctica al considerar el factor de potencia. El factor de potencia debe tenerse en cuenta cada vez que una compañía eléctrica conecta las líneas eléctricas a una planta de fabricación. Las industrias deben mantener el factor de potencia de sus circuitos y motores dentro de los límites especificados o pagar una prima a la compañía eléctrica.

La potencia reactiva a veces se denomina potencia de acacia. Se devuelve al circuito. yo Imagen 8, la potencia se utiliza en las áreas sombreadas por encima de la línea cero. El poder debajo de la línea es el poder de la acacia.

Ley de Ohm para circuitos AC

Al calcular los valores del circuito en circuitos de corriente alterna, Ley de Ohm usado con una excepción. Se usa Z en lugar de R. Z representa la fuerza resistiva total contra la corriente. Por lo tanto:

[begin{matrix}   I=frac{E}{Z} & and & begin{matrix}   E=Itimes Z & and & Z=frac{E}{I}  end{matrix}  end{matrix}]

Un ejemplo de la Ley de Ohm

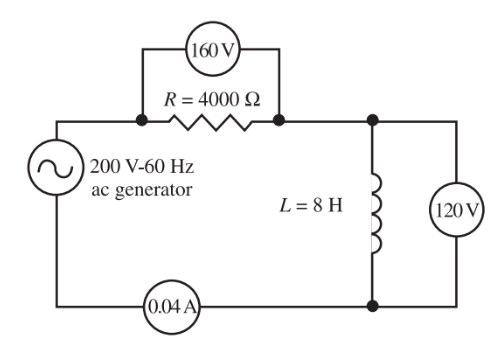
Un estrangulador de 8 Henry y una resistencia de 4000 ohmios están en un circuito en serie. Se conecta a través de una fuente de CA de 200 voltios y 60 Hz. Encuentre la impedancia, la corriente del circuito, las caídas de tensión en la resistencia y la inductancia, el ángulo de fase ( ), la potencia aparente y la potencia real. Mira Figura 9.

Imagen 9. Un circuito con un estrangulador de 8 Henry, una resistencia de 4000 ohmios conectada a través de una fuente de CA de 200 voltios y 60 Hz.

Primero, encuentre la reactancia de L.

${{X}_{L}}=2pi fL=2pi *60Hz*8H=3014Omega $

Encuentre la impedancia del circuito.

$Z=sqrt{{{R}^{2}}+X_{L}^{2}}=sqrt{{{4000}^{2}}+{{3000}^{2}}}= 5000Omega$

Encuentre la corriente en el circuito.

[I=frac{E}{Z}=frac{200V}{5000Omega }=0.04A]

Encuentre la caída de voltaje entre R y X_L.

$begin{align} & {{E}_{R}}=I*R=0.04A*4000Omega =160V & {{E}_{{{X}_{L}}}}= Yo *{{X}_{L}}=0.04A*3000Omega =120V end{align}$

Tenga en cuenta que la suma de las caídas de tensión no es igual a la tensión aplicada. Esto se debe a que los dos voltajes están desfasados ​​90 grados. Esto requiere agregar vectores.

$Fuentetext{ }Voltaje={{E}_{S}}=sqrt{{{160}^{2}}+{{120}^{2}}}=200V$

Encuentre el ángulo de fase θ entre I y E.

$begin{align} & cos theta =frac{R}{Z}=frac{4000Omega }{5000Omega }=0.8 & theta =co{{s}^{-1 }}left( 0.8 right)={{37}^{o}} end{align}$

Encuentre la potencia real y la potencia aparente.

• La corriente total se compensará con la subtensión en un ángulo entre 0 y 90 grados.
• Si la reactancia del inductor es mayor que la resistencia del resistor, el ángulo estará más cerca de 0 grados.
• Si la resistencia es mucho mayor que la reactancia, el desplazamiento estará más cerca de los 90 grados.

En el circuito paralelo RL, no encontramos la impedancia por suma vectorial. En su lugar, aplicamos la Ley de Ohm.

[Z=frac{{{E}_{S}}}{{{I}_{T}}}]

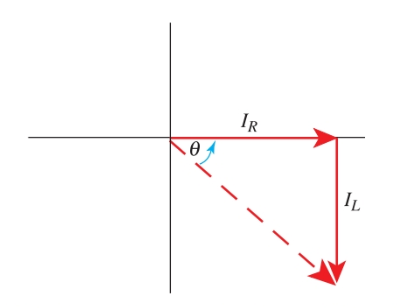
Como se muestra, el voltaje en el circuito paralelo RL está en fase con IR y conduce I_L de 90 grados. Entonces podemos decir que soy_R conduzco_L de 90 grados.

Por lo tanto, hay dos componentes de corriente en el circuito paralelo RL - I_R y yo mismo_L. Ambos elementos pueden ser representados por transeúntes. Como están desfasados, no podemos sumar los dos componentes para calcular la corriente total del circuito. Necesitamos obtener la suma del fáser. Mira Imagen 10.

${{I}_{T}}=raíz cuadrada{I_{R}^{2}+I_{L}^{2}}$

Tenga en cuenta que el fasor para I_L que está por debajo de la referencia horizontal. Es sobre mi_L voltaje de retardo - la referencia horizontal para el circuito paralelo RL. (Dado que un fasor, o vector giratorio, gira en sentido contrario a las agujas del reloj, un fasor quedaría detrás de un fasor principal, o aproximadamente en el sentido de las agujas del reloj).

Imagen 10. Diagrama fasorial que muestra la relación de θ con I_R y yo mismo_contra.

Definición del ángulo de fase

El ángulo de fase representa el cambio de fase entre corriente y voltaje como resultado de un elemento de circuito reactivo.

Para el circuito RL paralelo, el ángulo de fase está en el diagrama fasorial actual. La referencia horizontal de este circuito es el voltaje ya que es común a todos los elementos del circuito.

En el diagrama fasorial de corriente no tenemos fasor de tensión. Usamos IR como componente horizontal porque está en fase con el voltaje, Figura 10. Usando este diagrama, el ángulo de fase se puede obtener de:

[theta =arctan left( frac{{{I}_{L}}}{{{I}_{R}}} right)]

Ejemplo de cálculo de impedancia

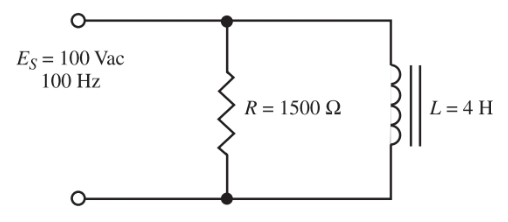
Usar el circuito con los valores ingresados Imagen 11, determine el ángulo de fase entre el voltaje y la corriente aplicados. Dibuje el diagrama de corriente fasorial y encuentre la impedancia del circuito.

Figura 11. Un circuito RL en paralelo.

Paso 1. Calcular el valor de la reactancia inductiva, X_L.

${{X}_{L}}=2pi fL=2pi *100Hz*4H=2512Omega $

2do grado Calcular corrientes de rama. Usando la Ley de Ohm:

$begin{alinear} & {{I}_{R}}=frac{{{E}_{S}}}{R}=frac{100V}{1500Omega }=0.067A & {{I}_{L} }=frac{{{E}_{S}}}{{{X}_{L}}}=frac{100V}{2512Omega }=0.04A end{alineación}$

Paso 3. Determine el ángulo de fase para determinar qué tan débil es la corriente del circuito con respecto al voltaje.

[theta =arctan left( frac{{{I}_{L}}}{{{I}_{R}}} right)=arctan left( frac{0.04}{0.067} right)={{30.8}^{o}}]

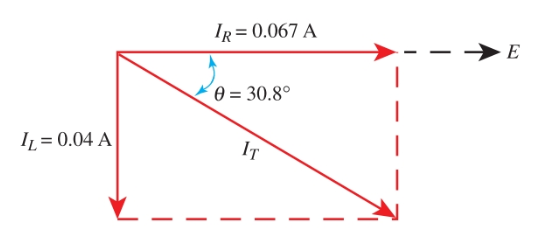
Paso 4. Dibuje un diagrama de fase de la corriente. Use cualquier escala conveniente. Recuerde que SI se dibuja como el componente horizontal. Un IT curvo se dibuja 90 grados hacia abajo desde IR porque retrasa el voltaje, la referencia horizontal. Mira Imagen 12.

Imagen 12. Diagrama fasorial de corriente.

Paso 5. Encuentre la corriente total del circuito.

${{I}_{T}}=sqrt{I_{R}^{2}+I_{L}^{2}}=sqrt{{{0.067}^{2}}+{{0.04} ^{2}}}=0.078A$

Paso 6. Encuentre la impedancia del circuito. Usando la Ley de Ohm:

[Z=frac{{{E}_{S}}}{{{I}_{T}}}=frac{100V}{0.078A}=1282Omega ]

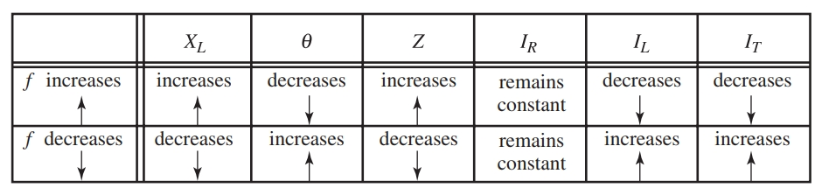
Una vez más, es importante entender cómo un cambio en la frecuencia afectaría las distintas cantidades. Los efectos del cambio de frecuencia se resumen i Imagen 13. Muestra cómo cambian los valores en un circuito RL paralelo cuando se cambia la frecuencia y la inductancia se mantiene en un valor constante.

Imagen 13. Esta tabla muestra el efecto sobre diferentes valores en un circuito RL en paralelo cuando se cambia la frecuencia mientras se mantiene constante el valor de la inductancia.