Cuando se aplica un voltaje alterno a un capacitor, las placas se cortan y descargan repetidamente. Durante la primera mitad del ciclo, las placas se cargan (una placa negativa y una placa positiva) y descargan a cero.
Durante el siguiente medio ciclo, las placas se cortan a las polaridades opuestas del primer medio ciclo y luego se descargan a cero. Un medidor de CA en el circuito siempre muestra la corriente que fluye.
Para demostrar este hecho, conecte una luz y un condensador en serie con una fuente de corriente continua de seis voltios, Figura 1. ¿La luz brilla?
Ahora conecte el mismo circuito a una fuente de CA de seis voltios. Tenga en cuenta que la luz se quema tenuemente. Este experimento muestra que fluye una corriente alterna debido a la carga y descarga alternas del capacitor.
Figura 1. Una luz no se enciende cuando se conecta a una fuente de CC. El condensador bloquea la corriente continua. Cuando esté conectado a una fuente de alimentación de CA, la luz se encenderá.
Para una revisión, consulte Figura 2. Cuando el voltaje de CA comienza a aumentar, la corriente es máxima porque el capacitor, C, está descargado. Cuando C se carga al voltaje máximo de CA, la corriente de carga cae a cero (punto A).
Cuando el voltaje comienza a caer, la corriente de descarga comienza a aumentar en dirección negativa. Alcanza un máximo en el punto de tensión cero (punto B). Esta diferencia de fase continúa a lo largo de cada ciclo. En un circuito capacitivo, la corriente adelanta al voltaje en un ángulo de 90 grados.
Figura 2. Cuando un circuito está conectado a corriente alterna, el voltaje aplicado, la corriente y el voltaje en C aparecen como se muestra.
Impedancia del condensador o reactancia capacitiva
La cantidad de corriente en el circuito depende del tamaño del capacitor. Los capacitores más grandes requieren más corriente (más capacitancia) para cargarse. La frecuencia de la tensión alterna también afecta a la corriente.
La corriente depende de la tasa de carga y descarga del capacitor. A medida que aumenta la frecuencia de la corriente alterna, aumenta la corriente. Estos enlaces se muestran en la fórmula:
[{{X}_{C}}=frac{1}{2pi fC}]
donde esta xcontra la reactancia es la capacitancia (o la impedancia del capacitor) en ohmios, f es la frecuencia en hercios y C es la capacitancia en faradios.
Al igual que los inductores, los capacitores producen resistencia a la corriente alterna. Esta resistencia que surge de la capacitancia se llama reactancia capacitiva (o impedancia del capacitor).
La reactancia capacitiva se mide en ohmios, como la resistencia de CC. Como se puede ver en la fórmula:
- Cuando la frecuencia aumenta, Xcontra
- Cuando el recurso aumenta, Xcontra
Ejemplo de cálculo de impedancia de condensador
¿Cuál es la reactancia (resistencia) de un capacitor de 10 μF que opera en un circuito a una frecuencia de 120 hercios?
[{{X}_{C}}=frac{1}{2pi fC}=frac{1}{2pi *left( 120Hz right)*left( 10*{{10}^{-6}}F right)}=132.7Omega ]
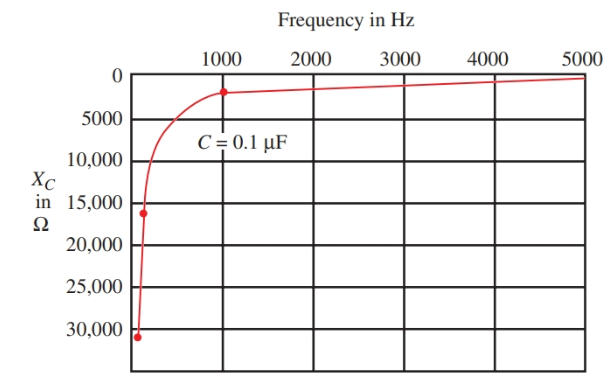
La reactancia de un capacitor de 0.1 μF a medida que cambia la frecuencia se puede ver i imagen 3. Cuando la frecuencia cambia a 50, 100, 1000 y 5000 Hz, todas las reactancias se calculan usando la fórmula de la reactancia de capacitancia (impedancia del capacitor). Observe cómo la reactancia en el gráfico se aproxima a cero a medida que la frecuencia tiende a infinito.
Imagen 3. A medida que aumenta la frecuencia, la reactancia capacitiva (impedancia del capacitor) disminuye.
En la Figura 4, la frecuencia se mantiene constante a 1000 Hz. La reacción se representa para condensadores de 0,01 μF, 0,05 μF, 0,1 μF y 0,5 μF. Estos son tamaños de capacitores comunes utilizados en trabajos electrónicos. Se utilizan en redes de filtrado, acoplamiento y bypass.
Figura 4. A medida que aumenta la capacitancia, disminuye la reactancia.
Potencia en un circuito capacitivo
Cuando se descarga un condensador, la energía almacenada en el dieléctrico se devuelve al circuito. Esta acción es similar a la de un inductor, que devuelve la energía almacenada en un campo magnético al circuito.
En ambos casos, el circuito reactivo utiliza energía eléctrica temporalmente. Esta potencia en un circuito capacitivo también se llama potencia de acacia.
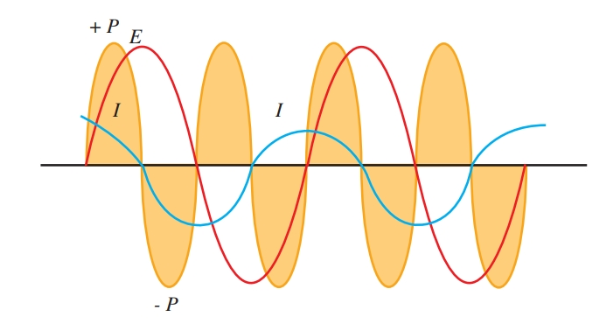
yo Figura 5, las formas de onda de voltaje y corriente se dibujan para un circuito que contiene capacitancia pura. La forma de onda de potencia resulta de graficar los productos del voltaje instantáneo y la corriente instantánea en puntos seleccionados.
Figura 5. Estas formas de onda representan corriente, voltaje y potencia en un solo circuito capacitivo.
La forma de onda de potencia muestra que el circuito utiliza cantidades iguales de potencia positiva y negativa. Esta condición da como resultado el uso de energía cero. La potencia real, o la potencia real utilizada, es entonces cero.
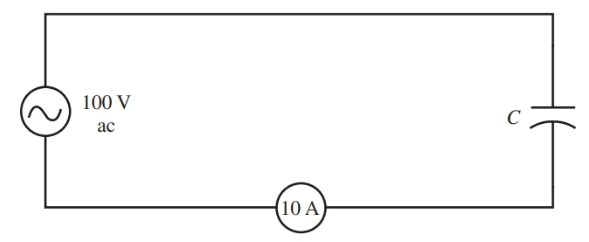
La potencia aparente es igual al producto de la tensión rms por la corriente rms. Para mirar Figura 6. Un voltaje alterno aplicado al circuito capacitivo crea una corriente de 10 amperios. La potencia aparente será igual a:
[begin{align} & Apparenttext{ }Power={{E}_{eff}}times {{I}_{eff}} & Apparenttext{ }Power=100Vtimes 10A=1000VA end{align}]
Factor de potencia
La relación entre la potencia real y la potencia aparente en un circuito de CA se denomina factor de potencia (PF).
Se encuentra usando trigonometría. Es el coseno del ángulo de fase entre la corriente y el voltaje.
[text{Power Factor=cos}theta text{=}frac{text{True Power}}{text{Apparent Power}}]
Ejemplo de factor de potencia
Suponiendo que nuestro circuito anterior es puramente capacitivo, determine el factor de potencia y el cambio de fase.
[text{Power Factor=cos}theta text{=}frac{0}{1000}=0]
El ángulo cuyo coseno es 0 es de 90 grados, lo que nos dice que la corriente y el voltaje en un solo circuito capacitivo están desfasados 90 grados.
Figura 6. Diagrama del circuito capacitivo teórico.
Resistencia y capacitancia en un circuito de CA
Cuando hay resistencia en un circuito, se utiliza la fuente de alimentación. Si solo hay resistencia en un circuito, entonces el voltaje y la corriente está en fase. No hay ángulo de fase θ y es un factor de potencia (cos 0° = 1). La potencia aparente es igual a la potencia real.
Estas características del circuito cambian cuando una capacitancia se coloca en serie con una resistencia. La reactancia capacitiva (impedancia del condensador) también es una fuerza que se opone al flujo de corriente alterna.
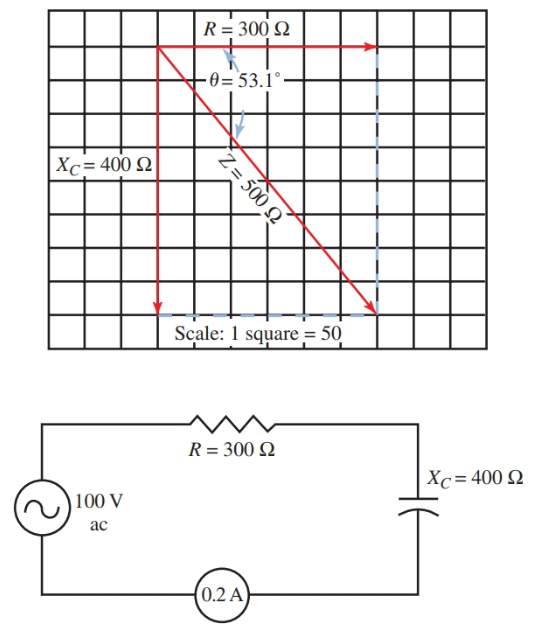
Dado que la reactancia capacitiva provoca un cambio de fase de 90 grados, la resistencia total a la corriente alterna debe ser el suma vectorial Xcontra y R. Estos vectores se dibujan en Imagen 7.
Suponiendo que el circuito de CA tiene una resistencia de 300 ohmios y una reactancia capacitiva (impedancia del capacitor) de 400 ohmios, la resistencia de corriente resultante es de 500 ohmios. Esta oposición se llama impedancia (Z)del circuito
$Z=sqrt{{{R}^{2}}+X_{C}^{2}}=sqrt{{{300}^{2}}+{{400}^{2}}}= 500Omega$
Imagen 7.
Alto. La relación vectorial entre R y Xcontra y el vector resultante, Z, para la barrera. Abajo. El circuito de CA para el problema del texto.
El ángulo entre el vector Z y el vector R representa el cambio de fase entre la corriente y el voltaje como resultado de la componente reactiva. Este es el ángulo θ. Como el coseno θ es igual al factor de potencia, podemos calcular usando:
[cos theta =PF=frac{R}{Z}=frac{300Omega }{500Omega }=0.6]
Son 53,1 grados (aprox.). Por lo tanto, la corriente se adelanta al voltaje en un ángulo de 53,1 grados.
La potencia real en este circuito es:
[text{True Power=Apparent Power}times cos theta ]
Es El factor de potencia es también la relación entre la potencia real y la potencia aparente. Como cos θ es igual al factor de potencia, se sigue que:
$begin{align} & Truetext{ }Potencia=Aparentementetext{ }Potenciaveces Potenciatext{ }Factor & o & PF=frac{Verdaderotext{ }Potencia}{ Aparente texto{ }Potencia} end{align}$
Usando Ley de Ohm para circuitos alternos, la corriente que fluye en la figura 7 (100 voltios alternos aplicados) es igual a:
[I=frac{E}{Z}=frac{100V}{500}=0.2A]
Entonces la potencia aparente es:
$Potencia aparente=I*E=0.2A*100V=20VA$
El verdadero poder es:
$Verdaderotext{ }Potencia=I*E*cos theta =0.2A*100V*cos {{53.1}^{o}}=12W$
Circuito RC en paralelo
- En un circuito de CA con una resistencia y un condensador en paralelo, el voltaje de cada elemento del circuito será el mismo que el voltaje de la fuente.
- Además, no habrá diferencia de fase entre los voltajes. Esto se debe a que todos son paralelos.
- Sin embargo, habrá una diferencia de fase entre la corriente completa y la corriente de rama. La corriente está en fase con el voltaje en la rama resistiva.
- La corriente impulsa el voltaje a través del capacitor 90 grados.
- La corriente total excede el voltaje de la fuente en un ángulo entre 0 y 90 grados.
- Si la reactancia del capacitor es mayor que la resistencia del resistor, θ estará más cerca de 0 grados. Si la resistencia es mucho mayor que la reactancia θ estará más cerca de los 90 grados.
- En el circuito RC en paralelo, no encontramos la impedancia por la suma vectorial de la resistencia del circuito. En cambio, aplicamos la ley de Ohm después de encontrar la suma de las corrientes de las ramas.
[Z=frac{{{E}_{S}}}{{{I}_{T}}}]
- Como se muestra, el voltaje en el circuito RC paralelo está en fase con IRy me atraecontra de 90 grados. Entonces podemos decir que soyR desacelerarcontra de 90 grados.
- Por lo tanto, hay dos componentes de corriente en el circuito paralelo RC - IR y yo mismocontra. Ambos elementos pueden ser representados por transeúntes. Como están desfasados, no podemos sumar los dos componentes para calcular la corriente total en el circuito. Necesitamos obtener la suma del fáser.
${{I}_{T}}=raíz cuadrada{I_{R}^{2}+I_{C}^{2}}$
- Tenga en cuenta que el fasor para Icontra por encima de la referencia horizontal. Es sobre micontra voltaje de plomo - la referencia horizontal para el circuito paralelo RC.
- Para el circuito RC en paralelo, el ángulo de fase está en el diagrama fasorial actual. La referencia horizontal de este circuito es el voltaje ya que es común a todos los elementos del circuito. En el diagrama de fase actual, I es el componente horizontalR ya que está en fase con el voltaje.
- Por lo tanto, el ángulo de fase es el ángulo entre IR y la corriente total. El cambio de fase es el resultado del elemento reactivo. En el circuito RC paralelo, el ángulo de fase es:
[theta =arctan left( frac{{{I}_{C}}}{{{I}_{R}}} right)]
Ejemplo de cálculo de ángulo de fase e impedancia
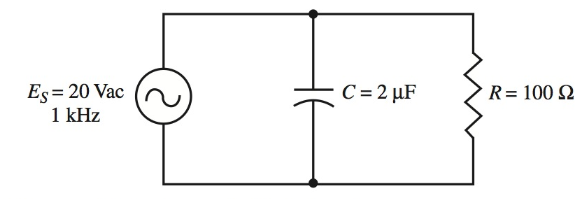
Uso del circuito de CA con valores nominales i Imagen 8, determine el ángulo de fase entre el voltaje y la corriente aplicados. Dibuje el diagrama de corriente fasorial y encuentre la impedancia del circuito.
Imagen 8. Circuito RC en paralelo.
Paso 1. Calcular el valor de la reactancia capacitiva, XC.
[{{X}_{C}}=frac{1}{2pi fC}=frac{1}{2pi *left( 1*{{10}^{3}} right)*left( 2*{{10}^{-6}} right)}=80Omega ]
2do grado Calcular corrientes de rama. Usando Ley de Ohm:
$begin{align} & {{I}_{R}}=frac{{{E}_{S}}}{R}=frac{20V}{100Omega }=0.2A & { {I}_{C}}=frac{{{E}_{S}}}{{{X}_{C}}}=frac{20V}{100Omega }=0.25A end {alinear}$
Paso 3. Determine el ángulo de fase para determinar cuánto adelanta la corriente del circuito al voltaje.
[theta =arctan left( frac{{{I}_{C}}}{{{I}_{R}}} right)=arctan left( frac{0.25}{0.2} right)={{51.3}^{o}}]
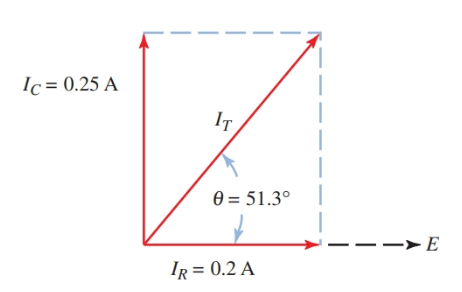
Paso 4. Dibuje un diagrama de fase de la corriente. Use cualquier escala conveniente. Recuerde que SI se dibuja como el componente horizontal. Un IC se dibuja a 90 grados del IR cuando se conduce un voltaje: la referencia horizontal. Consulte la figura 9.
Imagen 9. Diagrama fasorial de corriente.
Paso 5. Encuentre la corriente total del circuito.
[{{I}_{T}}=sqrt{I_{R}^{2}+I_{C}^{2}}=sqrt{{{0.2}^{2}}+{{0.25}^{2}}}=0.32A]
Paso 6. Encuentre la impedancia del circuito. Usando la Ley de Ohm:
[Z=frac{{{E}_{S}}}{{{I}_{T}}}=frac{20V}{0.32A}=62.5Omega ]
Todos los circuitos tienen una combinación de las tres propiedades eléctricas: R, L y C. Estas propiedades vienen en muchas configuraciones, incluyendo R, RLy antes de Cristo redes



¡Más Contenido!