Empleo y estabilidad
Si pyo es un polo de G(s), entonces la entrada natural o cero, la respuesta de G(s) consistirá en las funciones modales epagsyocontigo que noyo separar, y tq mipagsyocontigo, q = 0, 1, . . ., r – 1, si pyo el plural es r. Por lo tanto, la respuesta natural decaerá a cero si Re[pi] < 0 para i = 1, . . . , n, es decir, si todos los polos están en la mitad abierta a la izquierda del plano s, es decir, el semiplano izquierdo excluyendo el eje imaginario. Tal sistema se llama asintóticamente estable.
Si todos los polos en el semiplano abierto están a la izquierda excepto los polos individuales en el eje imaginario y en el origen, la respuesta natural consistirá en sinusoides no amortiguados o una constante distinta de cero, y se dice que el sistema es . algo estable.
Si algunos de los polos están en la mitad derecha del plano s o en el eje imaginario con una multiplicidad mayor que uno, entonces la respuesta natural será infinita y se dice que el sistema es inestable.
Determinar los polos de la función de transferencia.
Para G(s) dado en forma de TI, una función de MATLAB tf2zp se puede usar para encontrar los polos de G(s) y su estabilidad. Alternativamente, dado que solo estamos interesados en los polos, podemos aplicar la función de raíces polinómicas raíz al denominador de G(s) para encontrar sus polos. El siguiente ejemplo muestra el uso de raíces para determinar la estabilidad del sistema.
Estabilidad del sistema utilizando el ejemplo de Matlab
Encuentre los polos de la función de transferencia
$G(s)=frac{1.5s+1}{{{s}^{3}}+2{{s}^{2}}+2.5s+0.5}$
y determinar si el sistema es estable. Dibuja los polos y ceros de G(s) en el plano s. Finalmente, demuestre la estabilidad del sistema simulando la respuesta al impulso.
La solución
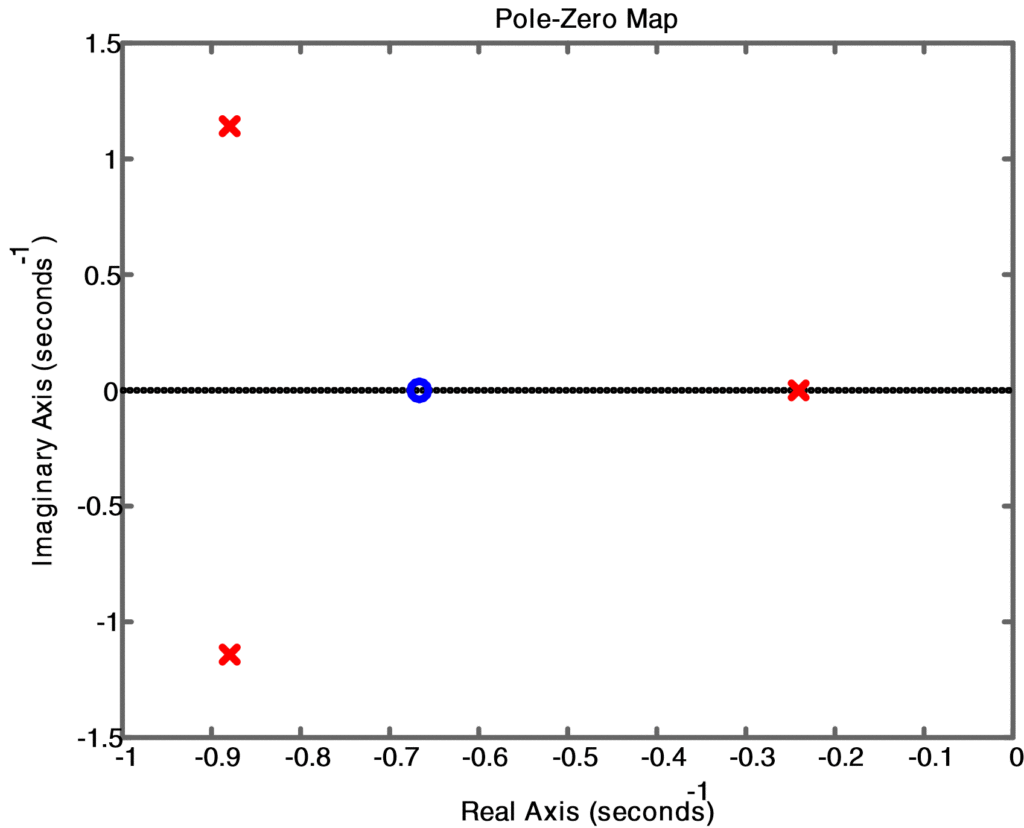
Establecer vectores de línea numG = [1.5 1] y de la G = [1 2 2.5 0.5] para representar el numerador y el denominador de G(s). Usando el comando raíces (de G), vemos que los polos de G(s) están en s = -0.2408 y -0.8796 ± j1.1414. Como todos los polos tienen partes reales negativas, es decir, todos están en el semiplano izquierdo abierto, el sistema asintóticamente estable. La respuesta al impulso se puede obtener del comando pulso (numG, denG)y disminuirá a cero como se muestra en la Figura 1. Los comandos de MATLAB en el script 7 calcularán los polos y ceros y crearán la gráfica como se muestra en la Figura 2.
Desde el comando raíces, obtuvimos el siguiente resultado:
| polacos |
| -0.8796+ 1.1414i |
| -0.8796 – 1.1414i |
| -0.2408 + 0.0000i |
Código de Matlab para encontrar polos y respuesta de impulso.
% Script 7: Matlab Code to find poles and impulse response clear all;close all;clc numG = [1.5 1]; % Create G(s) as a ratio of numerator &amp;amp;amp;amp; denumerator denG = [1 2 2.5 0.5]; roots(denG) % find poles of G(s) pzmap(numG,denG) % plot the poles and zeros impulse(numG,denG) % simulate impulse response
Resultados
Fig.1: Respuesta de impulso a una función de transferencia
Fig.2: Diagrama de polo cero para la estabilidad del sistema

¡Más Contenido!