Qué es un multiplicador binario: cómo funciona y sus aplicaciones

En los sistemas digitales, los circuitos lógicos combinatorios como el multiplicador binario, el sumador binario, el restador binario y la división binaria se utilizan para realizar operaciones aritméticas binarias como la multiplicación, suma, resta y división de dos números binarios '0' y '1'. Estos son ampliamente utilizados en diversas aplicaciones, como computadoras, móviles, calculadoras, procesadores de propósito general y procesadores de señales digitales para procesar la señal con varios algoritmos. Este artículo da una breve descripción de los tipos, reglas y métodos involucrados en la multiplicador binario para la multiplicación binaria.

¿Qué es un multiplicador binario?

Una definición de multiplicador binario es; un dispositivo electrónico o un dispositivo digital o un circuito lógico combinacional que realiza la multiplicación de dos números binarios (0 y 1). Los dos números binarios o las dos entradas binarias utilizadas en la multiplicación binaria son el multiplicando y el multiplicador para obtener el producto binario correspondiente.

El tamaño de bit del multiplicador y del multiplicando puede variar. Pero el tamaño de bit del producto binario depende del multiplicador y del tamaño de bit del multiplicando. La suma del multiplicador y el tamaño de bit del multiplicando es igual al tamaño de bit del producto binario final.

Función multiplicadora binaria

En el primer paso del proceso del multiplicador binario, los términos del producto parcial se obtienen mediante una multiplicación bit a bit, que es igual a la AND de dos números binarios. En el siguiente paso, todos los términos del producto parcial de cada columna se suman para obtener el resultado final del producto binario.

El diseño del circuito lógico de este multiplicador varía con el tamaño de bit y su complejidad aumenta con el aumento del tamaño de bit del multiplicador. Se rige por las funciones de la puerta AND cuando los dos bits, que deben multiplicarse, se alimentan como entradas con diferentes tamaños de bits.

La función principal de este multiplicador es hacer la multiplicación binaria de 2 números binarios con diferentes tamaños de bits y reducir el tiempo de cálculo en sistemas digitales electrónicos como computadoras. La multiplicación binaria es similar a la multiplicación decimal.

Reglas del multiplicador binario

Al igual que otras operaciones binarias, este multiplicador involucrado en la multiplicación binaria es mucho más fácil y similar a la multiplicación decimal. Hay multiplicadores y multiplicandos. El resultado de la multiplicación da el producto. Solo realiza la multiplicación binaria de números binarios (0 y 1), por lo que solo tiene que multiplicar 0 y 1. Estas son las reglas del multiplicador binario para la multiplicación binaria.

Regla 1: 0 × 0 = 0

Según esta regla, el producto binario de cero es él mismo igual a cero. Entonces el producto binario de cero y cero es cero.

Regla 2: 0 × 1 = 0

El producto binario de cero y uno es cero.

Regla 3: 1 × 0 = 0

El producto binario de uno y cero es cero.

Regla 4: 1 × 1 = 1 (Llevar o pedir prestado ningún objeto)

El producto binario de uno y uno es uno

Mesa de la verdad

los tabla de verdad de multiplicadores binarios se da a continuación.

Entrada A (Multiplicando)	Entrada B (multiplicador)	Salida C (producto binario)
0	0	0
0	1	0
0	0	0
1	1	1

Tipos de multiplicadores binarios

Estos son los tipos de multiplicadores binarios.

1) Multiplicador binario 2×2 o multiplicador de 2 bits.
– Multiplicador de 2 bits utilizando un sumador completo de 2 bits.
– Multiplicador de 2 bits utilizando sumadores individuales de un solo bit.
2) Multiplicador binario de 3×3 o multiplicador binario de 3 bits.
– Multiplicador binario de 3 bits utilizando sumadores completos de 3 bits.
– Multiplicador binario de 3 bits utilizando sumadores de un solo bit.
3) Multiplicador binario 4×4 o multiplicador de 4 bits.
– Multiplicador binario de 4 bits utilizando sumadores completos de 4 bits.

Multiplicador binario 3×3

Un multiplicador binario de 3×3 es uno de los circuitos lógicos combinacionales, que puede realizar la multiplicación binaria de dos números binarios con un tamaño de bit de un máximo de 3 bits. El tamaño de bits del producto binario de salida resultante es 6.

Considere el multiplicando A0 A1, A2 y el multiplicador B0, B1, B2, y la salida del producto binario final como P0, P1, P2. Los 3 términos del producto parcial se obtienen en la multiplicación binaria porque es un multiplicador de 3 bits. Este multiplicador de 3 × 3 se puede implementar utilizando un sumador completo de 3 bits y sumadores individuales de un solo bit. Considere el diseño del circuito lógico del multiplicador de 3 bits usando sumadores completos de 3 bits como se muestra en la figura a continuación.

A2 A1 A0 (multiplicando)
X B2 B1 B0 (multiplicador)
——————————————
A2B0 A1B0 A0B0
A2B1 A1B1 A0B1 X
A2B2 A1B2 A0B2XX
———————————————
A2B2+C+C A2B2+A1B2+A2B2+C+C A1B1+C+A0B2+A2B0 A0B1+A1B0 A0B

El bit de acarreo es alto cuando se agregan A2B0 y A1B1. Al sumar la suma obtenida de él, el bit de acarreo se obtiene al sumar A0B1 y A0B2 a A1B0, lo que puede generar otro bit de acarreo. Por lo tanto, se obtienen 2 bits de acarreo y se transfieren para la suma de A2B1 y A1B2 y los 2 bits de acarreo adicionales se generan de la misma manera.

Este método es muy simple en comparación con otros métodos. El circuito está diseñado con sumadores completos de 3 bits para sumar los 3 términos del producto parcial. El bit menos significativo (LSB) del 1er producto parcial no se suma al siguiente producto parcial porque se toma como LSB de la salida final del producto binario obtenido.

Del circuito lógico anterior, se usa un sumador completo de 3 bits para sumar los primeros 2 productos parciales y el otro sumador completo de 3 bits suma el tercer producto parcial con la suma del primer sumador.

El número de compuertas AND necesarias para el diseño del circuito se determina a partir de la fórmula m*n, donde 'm' es un multiplicador de bits y 'n' es un multiplicando de bits. El número de sumadores necesarios está determinado por la fórmula (m-1) para producir m+n bits. Entonces, este multiplicador de 3 bits requiere 9 puertas AND y dos sumadores completos de 3 bits.

Cuando se suman los tres términos del producto parcial, el LSB de la suma de cada sumador completo de 3 bits se toma directamente como salida, y los 3 bits restantes se suman al siguiente producto parcial.

Multiplicador binario usando el método Shift

Como alternativa al circuito multiplicador binario paralelo, se puede implementar un método de multiplicación manual usando un sumador de n bits, 4 registros (A, B, C y Q), lógica de desplazamiento y control como se muestra a continuación.

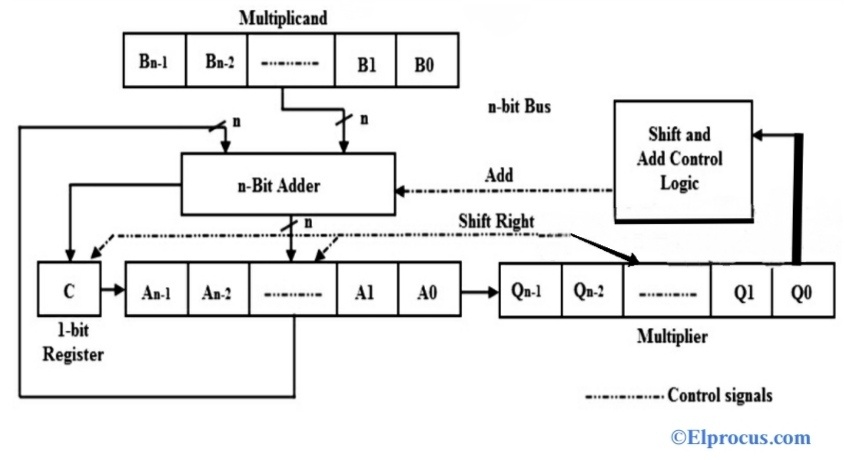
En este método, el multiplicador de 4 bits se almacena en el registro Q, el multiplicando de 4 bits se almacena en el registro B y el registro A se establece inicialmente en cero. El proceso de multiplicación comienza comprobando si el LSB (bit menos significativo) del número B es 0 o 1.

Si B0 = 1, el número del multiplicando (B) se suma al LSB del registro A y todos los bits de los registros C, A y Q se desplazan ligeramente hacia la derecha un bit.

Si el bit B0 = 0, la combinación de registros C y Q se desplaza un bit a la derecha sin procesamiento adicional. Este proceso se repite n veces para n bits. Este método de multiplicación binaria se llama multiplicación paralela usando el método de cambio o multiplicador binario usando el método de cambio.

Considere la siguiente figura, donde los valores del multiplicador y del multiplicando se muestran como 1011 y 1101, que se cargan en los registros Q y A, respectivamente. El registro C se establece en 0 inicialmente, por lo que el registro A también es 0 y el acarreo se almacena adicionalmente.

Como B0 = 1, sumamos el número en B a los bits en A, entonces el resultado de la suma es 1101, y los registros Q y A se desplazan 1 bit a la derecha para que los nuevos valores en el primer ciclo son 0110 y 1101 Debe repetir este proceso 4 veces para realizar una multiplicación de 4 bits. El resultado final de la multiplicación está disponible como 10001111 en los registros A y Q, como se muestra.

Un multiplicador binario 4 × 4 sin signo toma dos entradas de 4 bits para producir una salida de 8 bits. De manera similar, un multiplicador de 8 × 8 produce una salida de 16 bits al tomar dos entradas de 8 bits. Este multiplicador con circuitos lógicos se implementa en circuitos integrados (IC) con diferentes configuraciones de pines, utilizados para varias aplicaciones de microprocesadores como dispositivos de control, computadoras, móviles, calculadoras, DSP y muchos otros.

Multiplicador binario usando el gráfico ASM

El multiplicador binario que utiliza el diagrama de Máquinas de estado de algoritmo (ASM) implementa el algoritmo de multiplicación binaria como se muestra en la siguiente figura.

Según el algoritmo anterior, se indica '<<' para la asignación. Por ejemplo, 'C<<0' significa que 'C está establecido en 0'.

En este proceso, se utilizan 3 estados como IDLE, MUL0 y MUL1 para proporcionar señales de control a la ruta de datos para realizar secuencias de multiplicación. El proceso comienza con la entrada 'G'. El ASM permanece en un estado INACTIVO siempre que G siga siendo MUL0. El proceso de multiplicación binaria comienza cuando G=1. Cuando el ASM pasa al estado MUL0, el flip-flop de acarreo y el registro A se borran (C<<0 y A<<0), el contador se preestablece en n-1 (P

En el estado MUL0, el valor de cada bit del multiplicador (disponible en Q0) determina si el multiplicando se suma (Q0=1) o no (Q0=0). Si Q0 = 0, entonces se borra el pestillo de acarreo. Si Q0 = 1, entonces el pestillo de acarreo almacena el Cout (salida de acarreo) obtenido del sumador.

En el estado MUL1, el flip-flop de acarreo, el registro A y el registro Q se designan como registros de bits (1+n+n) y juntos se desplazan una posición a la derecha. En la tabla ASM, esto se indica mediante C|A|Q

• Devuelve el estado MUL0 (si Z=0) para el resto de la iteración o
• Vuelva al estado INACTIVO (si Z=1) para completar el proceso. Tenga en cuenta que si Z=1, el contador cuenta hacia atrás de n-1 a 0 y, por lo tanto, completa las iteraciones n.

Si el estado IDLE = 0, entonces el multiplicador se indica para 'ser multiplicado'. Si IDLE=1, (la tarjeta ASM vuelve a IDLE=1), esto indica que el proceso de multiplicación binaria está completo.

En este punto del proceso de diseño, se identifican las señales de control. Esto se puede hacer observando la ruta de datos y el gráfico ASM. La siguiente tabla muestra todas las operaciones realizadas en cada componente de la ruta de datos con los nombres de las señales de control correspondientes.

Componente de ruta de datos	Operación	Nombre de la señal de controlson
usar chanclas	C<<0, C	Borrar_C Cargar
P-metro	PAGS	Inicializar May_dic
registro A	un<<0 POSEE C|A|Q	Inicializar Pan May_dic
Guardar Q	q C|A|Q	Inicializar May_dic

Diagrama de bloques del multiplicador binario

El proceso de multiplicación binaria se divide en dos componentes, como la ruta de datos y la lógica de control/controlador. Este diagrama de bloques multiplicador con ruta de datos y lógica de control se muestra en la siguiente figura.

La ruta de datos se utiliza para manipular datos de acuerdo con los requisitos del sistema. La lógica de control o la unidad de control o el controlador se usa para generar las señales para secuenciar las operaciones en el procesador de datos.

Del diagrama de bloques anterior, podemos observar que,

Datos de entrada: Multiplicando (n bits) y multiplicador (n bits)

Datos resultantes: Producto binario (2n bits)

Señales de control del controlador o comandos: Borrar acarreo, Cargar, Desplazar y Borrar para cada registro de desplazamiento e Inicializar (para el contador).

Condiciones de estado: Z (detección de cero) y Q0 (multiplicador de cada bit)

Código Verilog del multiplicador binario

Echemos un vistazo al código Verilog del multiplicador binario 2 × 2 en Modelado de flujo de datos y Modelado de comportamiento.

Multiplicador binario 2×2 en el modelado de flujo de datos:

biblioteca ieee;
use ieee.std_logic_1164.all;

entidad multiplicar es
puerto(A,B: en bit_vector(1 a 0);
P: fuera bit_vector (3 a 0)
);
terminar multiplicar;

el flujo de datos de la arquitectura de la multiplicación es
comenzar
P(0) <= A(0) Y B(0);
P(1) <= (A(1) Y B(0)) XOR (A(0) Y B(1));
P(2) <= ((A(1) Y B(0)) Y (A(0) Y B(1))) XOR (A(1) Y B(1));
P(3) <= ((A(1) Y B(0)) Y (A(0) Y B(1))) Y (A(1) Y B(1));
arquitectura final;

Multiplicador binario de código Verilog 2 × 2 en modelado de comportamiento

biblioteca ieee;
use ieee.std_logic_1164.all;
la entidad multiplicar_comportamiento es
puerto(A,B:en bit_vector(1 a 0);
P: fuera bit_vector (3 a 0);
terminar multiplicar_comportamiento;

comienza la arquitectura de comportamiento de multiplicador_comportamiento

proceso (A, B) es
comenzar
el caso A es
cuando "00"=>
si B=”00″ entonces P<=”0000″;
de lo contrario si B=”01″ entonces P<=”0000″;
de lo contrario si B=”10″ entonces P<=”0000″;
de lo contrario P<="0000";
terminara si;

cuando "01"=>
si B=”00″ entonces P<=”0000″;
de lo contrario si B=”01″ entonces P<=”0001″;
de lo contrario si B=”10″ entonces P<=”0010″;
de lo contrario P<="0011";
terminara si;

cuando "10"=>
si B=”00″ entonces P<=”0000″;
de lo contrario si B=”01″ entonces P<=”0010″;
de lo contrario si B=”10″ entonces P<=”0100″;
de lo contrario P<="0110";
terminara si;

cuando "11" =>
si B=”00″ entonces P<=”0000″;
de lo contrario si B=”01″ entonces P<=”0011″;
de lo contrario si B=”10″ entonces P<=”0110″;
de lo contrario P<="1001";
terminara si;

fin del caso;

proceso final;
arquitectura final;

Ventajas

los beneficios del multiplicador binario se dan a continuación.

• Los términos de productos intermedios o términos de productos parciales se generan muy fácilmente y son simples.
• Multiplica el multiplicando con el multiplicador de diferentes tamaños de bits y se puede cambiar el rango de sus tamaños de bits.
• Ayuda a reducir el tiempo necesario para procesar la señal digital con algoritmos en procesadores de señal.
• Disponible en pequeños circuitos integrados para aplicaciones electrónicas comerciales como ordenadores, móviles, calculadoras y procesadores.
• El diseño del circuito es simple en comparación con los sumadores binarios y los restadores binarios.
• El costo es bajo.

Aplicaciones

los aplicaciones de multiplicador binario están enlistados debajo:

• Utilizado en computadoras.
• Utilizado en móviles.
• Se utiliza en calculadoras de alta velocidad.
• Utilizado en procesadores de señal. digital.
• Se utiliza en el control de dispositivos.
• Utilizado en sistemas de comunicación digital.

1). ¿Qué es un multiplicador binario en VHDL?

El programa VHDL para este multiplicador se puede escribir de 3 formas. Ellas son,

• Uno es el modelado de flujo de datos, que describe el flujo de datos a través de cada puerta lógica mediante ecuaciones.
• El modelado de comportamiento define el comportamiento de la entidad usando instrucciones secuenciales
• El modelado estructural describe el circuito utilizando las interconexiones de los componentes individuales del circuito.

2) ¿Qué se necesita para implementar un multiplicador binario de 2 bits?

El multiplicador binario de 2 bits se implementa usando 2 compuertas XOR y 6 compuertas AND en total o puede implementarse usando 4 compuertas AND y 2 medios sumadores.

Así, se trata de una descripción general de un multiplicador binario utilizado en varios dispositivos electrónicos. Aquí se utiliza una calculadora multiplicadora binaria para realizar la multiplicación binaria de 2 formatos de números binarios de forma muy rápida y sencilla sin utilizar ningún método manual. Aquí hay una pregunta para usted, ¿qué es un gráfico ASM?