Suma de productos y producto de sumas
Las diferentes formas de expresión canónica que incluyen la suma de productos (SOP) y los productos de la suma (POS), La expresión canónica puede definirse como una expresión booleana que tiene un término mínimo o un término máximo. Por ejemplo, si tenemos dos variables, X e Y, la expresión canónica compuesta por términos mínimos será XY+X'Y', mientras que la expresión canónica compuesta por términos máximos será (X+Y) (X'+Y'). En este artículo se trata una visión general de la suma de productos y el producto de sumas, los tipos de SOP y POS, el diseño esquemático y el mapa K.
Suma de productos y producto de sumas
El concepto de suma de productos (SOP) incluye principalmente el término mínimo, los tipos de SOP, el mapa K y el diseño esquemático de SOP. Del mismo modo, el producto de sumas (POS) incluye principalmente el término máximo, tipos de producto de sumas, mapa k y diseño esquemático del TPV.
¿Qué es una suma de productos (SOP)?
La forma abreviada de la suma del producto es SOP, y es un tipo de Álgebra booleana expresión. En ella, se suman las diferentes entradas del producto. El producto de las entradas es el AND lógico booleano, mientras que la suma o adición es el OR lógico booleano. Antes de entender el concepto de suma de productos, tenemos que conocer el concepto de minitérmino.
El min plazo se puede definir como, cuando las combinaciones mínimas de entradas son altas, entonces la salida será alta. El mejor ejemplo de esto es la puerta AND, por lo que podemos decir que los términos min son combinaciones de entradas de la puerta AND. La tabla de verdad del término mínimo se muestra a continuación.
|
X |
Y | Z |
Término mínimo (m) |
|
0 |
0 |
0 |
X'Y'Z' = m0 |
|
0 |
0 | 1 |
X'Y'Z = m1 |
|
0 |
1 | 0 | X'Y Z' = m2 |
| 0 | 1 | 1 |
X'YZ = m3 |
| 1 | 0 | 0 |
XY'Z'= m4 |
|
1 |
0 | 1 | XY'Z = m5 |
| 1 | 1 | 0 |
XYZ' = m6 |
| 1 | 1 | 1 |
XYZ = m7 |
En la tabla anterior, hay tres entradas: X, Y y Z, y las combinaciones de estas entradas son 8. Cada combinación tiene un minitérmino que se especifica con m.
Tipos de suma de productos (SOP)
El suma de productos está disponible en tres formas diferentes que incluyen las siguientes.
- Suma canónica de productos
- Suma no canónica de productos
- Suma mínima de productos
1). Suma canónica de productos
Se trata de una forma normal de SOP, y se puede formar con la agrupación de los minterms de la función para la que el o/p es alto o verdadero, y también se denomina suma de minterms. La expresión del SOP canónico se denota con la suma de signos (∑), y los minterms del paréntesis se toman cuando la salida es verdadera. La tabla de verdad de la suma canónica del producto se muestra a continuación.
|
X |
Y | Z |
F |
|
0 |
0 | 0 | 0 |
| 0 | 0 | 1 |
1 |
|
0 |
1 | 0 | 1 |
| 0 | 1 | 1 |
1 |
|
1 |
0 | 0 | 0 |
| 1 | 0 | 1 |
1 |
|
1 |
1 | 0 | 0 |
| 1 | 1 | 1 |
0 |
Para la tabla anterior, el forma canónica SOP puede escribirse como F = ∑ (m1, m2, m3, m5)
Expandiendo la suma anterior podemos obtener la siguiente función
F = m1 + m2 + m3 + m5
Sustituyendo los minterms en la ecuación anterior podemos obtener la siguiente expresión
F = X'Y'Z + X'YZ' + X'YZ + XY'Z
El término del producto de la forma canónica incluye tanto las entradas complementadas como las no complementadas
2). Suma no canónica de productos
En la forma de suma no canónica de productos, los términos del producto se simplifican. Por ejemplo, tomemos la expresión canónica anterior.
F = X'Y'Z + X'YZ' + X'YZ + XY'Z
F = X'Y'Z + X'Y (Z'+Z) + XY'Z
Aquí Z'+Z =1 (Función estándar)
F = X'Y'Z + X'Y (1) + XY'Z
F = X'Y'Z + X'Y + XY'Z
Esto sigue siendo la forma de SOP, pero es la forma no canónica
3). Suma mínima de productos
Esta es la expresión más simplificada de la suma del producto, y también es un tipo de lata no canónica. Este tipo de lata se simplifica con los teoremas algebraicos booleanos, aunque se hace simplemente utilizando Mapa K (mapa de Karnaugh).
Esta forma se elige porque el número de líneas de entrada y de compuertas utilizadas es mínimo. Es rentable por su tamaño sólido, su velocidad rápida y su bajo precio de fabricación.
Tomemos un ejemplo de función de forma canónica, y el mínimo Mapa de suma de productos K es
La expresión de esto basada en el mapa K será
F = Y'Z + X'Y
Diseño esquemático de la suma del producto
La expresión de la suma del producto ejecuta un diseño AND-OR de dos niveles, y este diseño requiere una colección de puertas AND y una puerta OR. Cada expresión de la suma del producto tiene un diseño similar.

El número de entradas y el número de puertas AND dependen de la expresión que se esté implementando. El diseño para una suma mínima de producto y expresión canónica utilizando puertas AND-OR se muestra arriba.
¿Qué es un producto de suma (POS)?
La forma abreviada del producto de la suma es POS, y es un tipo de expresión del álgebra booleana. Se trata de una forma en la que se toman los productos de la suma disímil de entradas, que no son resultado aritmético y suma, aunque sí son lógicos booleanos Y y O correspondientes. Antes de pasar a entender el concepto de producto de la suma, tenemos que conocer el concepto de término máximo.
El término max puede definirse como un término que es verdadero para el mayor número de combinaciones de entrada, o que es falso para las combinaciones de entrada únicas. Porque la puerta OR también es falsa para una sola combinación de entrada. Por tanto, el maxterm es el OR de cualquier entrada complementada o, de lo contrario, no complementada.
|
X |
Y | Z | Término máximo (M) |
|
0 |
0 | 0 |
X+Y+Z = M0 |
| 0 | 0 | 1 |
X+Y+Z' = M1 |
|
0 |
1 | 0 | X+Y'+ Z = M2 |
| 0 | 1 | 1 |
X+Y'+Z' = M3 |
|
1 |
0 | 0 | X'+Y+Z= M4 |
| 1 | 0 | 1 |
X'+Y+Z' = M5 |
|
1 |
1 | 0 | X'+Y'+Z = M6 |
| 1 | 1 | 1 |
X'+Y'+Z' = M7 |
En la tabla anterior, hay tres entradas: X, Y y Z, y las combinaciones de estas entradas son 8. Cada combinación tiene un término máximo que se especifica con M.
En el término máximo, cada entrada se complementa, ya que sólo proporciona "0" mientras se aplica la combinación indicada, y el complemento del término mínimo es un término máximo.
M3 =m3'
(X'YZ)' = M3
X+Y'+Z'=M3 (Ley de Morgan)
Tipos de Producto de Sumas (POS)
El producto de la suma se clasifica en tres tipos que son los siguientes
- Producto canónico de las sumas
- Producto no canónico de sumas
- Producto mínimo de sumas
1). Producto canónico de sumas
El POS canónico también se denomina producto de término máximo. Se trata de un AND conjunto para el que o/p es bajo o falso. La expresión esto se denota con ∏ y los términos max en el paréntesis se toman cuando la salida es falsa. La tabla de verdad del producto canónico de la suma se muestra a continuación.
|
X |
Y | Z | F |
| 0 | 0 | 0 |
0 |
|
0 |
0 | 1 | 1 |
| 0 | 1 | 0 |
1 |
|
0 |
1 | 1 | 1 |
| 1 | 0 | 0 |
0 |
| 1 | 0 | 1 |
1 |
|
1 |
1 | 0 | 0 |
| 1 | 1 | 1 |
0 |
Para la tabla anterior, el TPV canónico puede escribirse como F = ∏ (M0, M4, M6, M7)
Expandiendo la ecuación anterior podemos obtener la siguiente función
F = M0, M4, M6, M7
Sustituyendo los términos máximos en la ecuación anterior podemos obtener la siguiente expresión
F = (X+Y+Z) (X'+Y+Z)(X'+Y'+Z)(X'+Y'+Z')
El término del producto de la forma canónica incluye tanto las entradas complementadas como las no complementadas
2). Producto no canónico de la suma
La expresión de la producto de la suma (POS) no está en forma normal se denomina forma no canónica. Por ejemplo, tomemos la expresión anterior
F = (X+Y+Z) (X'+Y+Z)(X'+Y'+Z)(X'+Y'+Z')
F = (Y+Z) (X'+Y+Z) (X'+Y'+Z')
Similar aunque los términos invertidos eliminan de dos términos Max & forma única término para mostrarlo aquí es un ejemplo.
= (X+Y+Z) (X'+Y+Z)
= XX’+XY+XZ+X’Y+YY+YZ+X’Z+YZ+ZZ
= 0+XY+XZ+X'Y+YY+YZ+X'Z+YZ+Z
= X (Y+Z) + X' (Y+Z) + Y(1+Z) +Z
= (Y+Z) (X+X') + Y (1) +Z
= (Y+Z) (0) +Y+Z
= Y+Z
La expresión final anterior sigue estando en la forma de Producto de la Suma; sin embargo, está en la forma no canónica.
3). Producto mínimo de sumas
Esta es la expresión más simplificada del producto de la suma, y también es un tipo de no canónico. Este tipo de lata se simplifica con los teoremas algebraicos booleanos, aunque se hace simplemente utilizando el mapa K (mapa de Karnaugh).
Esta forma se elige debido a que el número de líneas de entrada y puertas que se utilizan en ella es mínimo. Es rentable debido a su sólido tamaño, su rápida velocidad y su bajo precio de fabricación.
Tomemos un ejemplo de función de forma canónica, y el Producto de sumas K mapa es
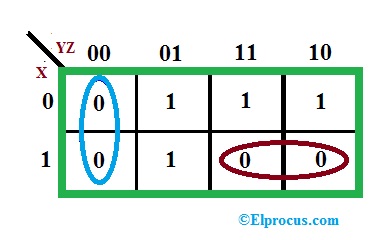
La expresión de esto basada en el mapa K será
F = (Y+Z) (X'+Y')
Diseño esquemático del producto de la suma
La expresión del producto de la suma ejecuta un diseño OR- AND de dos niveles y este diseño requiere una colección de puertas OR y una puerta AND. Cada expresión del producto de la suma tiene un diseño similar.
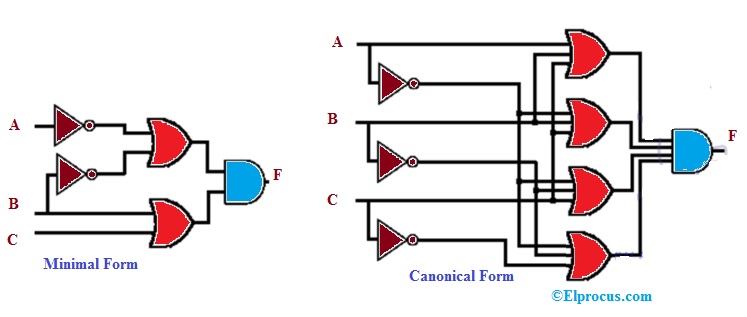
El número de entradas y el número de puertas AND dependen de la expresión que se esté implementando. El diseño para una suma mínima de producto y expresión canónica utilizando puertas OR-AND se muestra arriba.
Por tanto, se trata de Formas canónicas: Suma de productos y producto de sumas, diseño esquemático, mapa K, etc. De la información anterior, finalmente, podemos concluir que una expresión booleana está formada completamente por cualquiera de los mintérminos o, de lo contrario, los maxtérminos se denominan expresión canónica. Aquí tienes una pregunta, ¿cuáles son las dos formas de expresiones canónicas?
Si quieres conocer otros artículos parecidos a Suma de productos y producto de sumas puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!