Sumador de arrastre de ondas : Funcionamiento, tipos y sus aplicaciones
En la electrónica digital, la adición de números binarios de dos bits puede realizarse mediante el uso de un medio sumador. Y si la secuencia de entrada tiene una secuencia de tres bits, el proceso de adición puede completarse utilizando un sumador completo. Pero si el número de bits es mayor en la secuencia de entrada, el proceso puede completarse utilizando un medio sumador. Porque el sumador completo no puede completar la operación de suma. Así que estos inconvenientes pueden superarse utilizando el "sumador de acarreo ondulado". Es un tipo único de circuito lógico utilizado para sumar números de N bits en operaciones digitales. Este artículo describe una visión general de lo que es el sumador de arrastre por ondulación y su funcionamiento.
-
¿Qué es el sumador de arrastre por ondulación?
- sumador de arrastre por ondulación de 4 bits
- sumador de acarreo ondulado de 8 bits
- sumador de arrastre de ondulación de 16 bits
- Tabla de verdad del sumador de arrastre de ondas
- Código VHDL del sumador de acarreo ondulado
- Código Verilog del sumador de acarreo ondulado
- Aplicaciones del sumador de acarreo ondulado
- Ventajas del sumador de arrastre de ondas
¿Qué es el sumador de arrastre por ondulación?
Se trata de una estructura de múltiples sumadores completos conectados en cascada para obtener los resultados de la suma de una secuencia binaria de n bits. Este sumador incluye sumadores completos en cascada en su estructura, por lo que el acarreo se generará en cada etapa del sumador completo en un circuito sumador de acarreo por ondulación. La salida del acarreo en cada etapa del sumador completo se transmite al siguiente sumador completo y se aplica como entrada de acarreo. Este proceso continúa hasta la última etapa del sumador completo. Así pues, cada bit de salida de acarreo se riega a la siguiente etapa de un sumador completo. Por esta razón, se denomina "Sumador de arrastre ondulado". La característica más importante de este sumador es que permite sumar las secuencias de bits de entrada, tanto si la secuencia es de 4 bits como de 5 bits o cualquiera.
"Uno de los puntos más importantes que hay que tener en cuenta en este sumador de arrastre es que la salida final sólo se conoce después de que cada etapa del sumador completo genere las salidas de arrastre y las envíe a su siguiente etapa. Por lo tanto, habrá un retraso en la obtención del resultado con el uso de este sumador de arrastre".
Hay varios tipos de sumadores de arrastre de ondas. Son:
- sumador de 4 bits de arrastre de ondas
- sumador de 8 bits de arrastre de ondas
- sumador de 16 bits de arrastre de ondas
En primer lugar, empezaremos con la escalera de ondulación de 4 bits y luego con los sumadores de ondulación de 8 y 16 bits.
sumador de arrastre por ondulación de 4 bits
El siguiente diagrama representa el sumador de arrastre por ondulación de 4 bits. En este sumador, se conectan cuatro sumadores completos en cascada. Co es el bit de entrada de acarreo y es siempre cero. Cuando este acarreo de entrada 'Co' se aplica a las dos secuencias de entrada A1 A2 A3 A4 y B1 B2 B3 B4, la salida se representa con S1 S2 S3 S4 y el acarreo de salida C4.
Funcionamiento de la sumadora de arrastre de 4 bits
- Tomemos un ejemplo de dos secuencias de entrada 0101 y 1010. Éstas representan el A4 A3 A2 A1 y el B4 B3 B2 B1.
- Según este concepto de sumador, el acarreo de entrada es 0.
- Cuando se aplican Ao y Bo en el primer sumador completo junto con el acarreo de entrada 0.
- Aquí A1 =1 ; B1=0 ; Cin=0
- La suma (S1) y el acarreo (C1) se generarán según las ecuaciones de suma y acarreo de este sumador. Según su teoría, la ecuación de salida para la Suma = A1⊕B1⊕Cin y el Transporte = A1B1⊕B1Cin⊕CinA1
- Según esta ecuación, para el 1er sumador completo S1 =1 y la salida Carry, es decir, C1=0.
- Lo mismo que para los siguientes bits de entrada A2 y B2, la salida S2 = 1 y C2 = 0. Aquí el punto importante es que el sumador completo de la segunda etapa obtiene el acarreo de entrada, es decir, C1, que es el acarreo de salida del sumador completo de la etapa inicial.
- De este modo se obtiene la secuencia de salida final (S4 S3 S2 S1) = (1 1 1 1) y el acarreo de salida C4 = 0
- Este es el proceso de adición para las secuencias de entrada de 4 bits cuando se aplica a este sumador de arrastre.
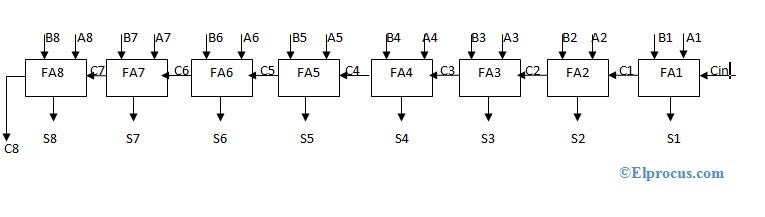
sumador de acarreo ondulado de 8 bits
- Consta de 8 sumadores completos conectados en cascada.
- Cada salida de acarreo del sumador completo se conecta como acarreo de entrada al sumador completo de la siguiente etapa.
- Las secuencias de entrada se denominan (A1 A2 A3 A4 A5 A6 A7 A8) y (B1 B2 B3 B4 B5 B6 B7 B8) y su correspondiente secuencia de salida se denomina (S1 S2 S3 S4 S5 S6 S7 S8).
- El proceso de adición en una escalera de rizos de 8 bits es el mismo principio que se utiliza en una escalera de rizos de 4 bits, es decir, cada bit de dos secuencias de entrada se va a sumar junto con el acarreo de entrada.
- Se utilizará cuando la suma de dos secuencias de dígitos binarios de 8 bits.
sumador de arrastre de ondulación de 16 bits
- Consta de 16 sumadores completos conectados en cascada.
- Cada salida de acarreo del sumador completo se conecta como acarreo de entrada al sumador completo de la siguiente etapa.
- Las secuencias de entrada se denominan (A1 ..... A16) y (B1 ...... B16) y su correspondiente secuencia de salida se denomina (S1 ........ S16).
- El proceso de adición en una escalera de rizos de 16 bits es el mismo principio que se utiliza en un sumador de rizos de 4 bits, es decir, cada bit de dos secuencias de entrada se va a sumar junto con el acarreo de entrada.
- Se utilizará cuando la suma de dos secuencias de dígitos binarios de 16 bits.
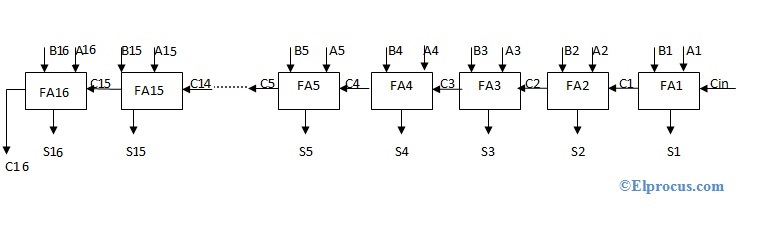
Tabla de verdad del sumador de arrastre de ondas
La siguiente tabla de verdad muestra los valores de salida para las posibles combinaciones de todas las entradas de la escalera de rizado.
| A1 | A2 | A3 | A4 | B4 | B3 | B2 | B1 | S4 | S3 | S2 | S1 |
Llevar |
|
0 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
0 |
|
1 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
1 |
Código VHDL del sumador de acarreo ondulado
VHDL (VHSIC HDL) es un lenguaje de descripción de hardware. Es un lenguaje de diseño digital. A continuación se muestra el código VHDL de este sumador de transportes.
biblioteca IEEE;
usa IEEE.STD_LOGIC_1164.ALL;
la entidad Ripplecarryadder es
Puerto ( A : en STD_LOGIC_VECTOR (3 hasta 0);
B: en STD_LOGIC_VECTOR (3 hasta 0);
Cin : en STD_LOGIC;
S: out STD_LOGIC_VECTOR (3 hasta 0);
Cout : out STD_LOGIC);
fin de la escalera de ripio;
el comportamiento de la arquitectura de Ripplecarryadder es - Declaración del componente del código VHDL del sumador completo
componente full_adder_vhdl_code
Puerto ( A : en STD_LOGIC;
B : en STD_LOGIC;
Cin : en STD_LOGIC;
S : out STD_LOGIC;
Cout : out STD_LOGIC);
fin del componente;
- Declaración de transporte intermedio
Señal c1,c2,c3: STD_LOGIC;
comenzar
- Mapeo de puertos Suma completa 4 veces
FA1: mapa de puertos full_adder_vhdl_code( A(0), B(0), Cin, S(0), c1);
FA2: full_adder_vhdl_code port map( A(1), B(1), c1, S(1), c2);
FA3: full_adder_vhdl_code port map( A(2), B(2), c2, S(2), c3);
FA4: full_adder_vhdl_code port map( A(3), B(3), c3, S(3), Cout);
fin Comportamiento;
Código Verilog del sumador de acarreo ondulado
El código Verilog es un lenguaje de descripción de hardware. Se utiliza en los circuitos digitales en la etapa RTL para el diseño y la verificación. A continuación se muestra el código verilog de este sumador de transportes.
módulo ripple_carry_adder(a, b, cin, sum, cout);
entrada [03:0] a;
entrada [03:0] b;
entrada cin;
salida [03:0] suma;
salida cout;
cable [2:0]c;
fulladd a1(a[0],b[0],cin, sum[0],c[0]);
fulladd a2(a[1],b[1],c[0],suma[1],c[1]);
fulladd a3(a[2],b[2],c[1],suma[2],c[2]);
fulladd a4(a[3],b[3],c[2],suma[3]cout);
endmodule
módulo fulladd(a,b,cin,sum,cout);
entrada a,b,cin;
salida suma,cout;
asignar suma=(a^b^cin);
assign cout=((a&b)|(b&cin)|(a&cin));
Aplicaciones del sumador de acarreo ondulado
Las aplicaciones de la escalera de arrastre por ondulación son las siguientes
- Estos sumadores de arrastre se utilizan sobre todo como complemento de las secuencias de entrada de n bits.
- Estos sumadores de arrastre son aplicables en el procesamiento digital de señales y en los microprocesadores.
Ventajas del sumador de arrastre de ondas
Las ventajas de la escalera de arrastre por ondulación son las siguientes
- Este sumador de arrastre tiene la ventaja de que podemos realizar el proceso de adición de secuencias de n bits para obtener resultados precisos.
- El diseño de este sumador no es un proceso complejo.
Sumador de acarreo ondulado es una alternativa para cuando el semi-sumador y los sumadores completos no realizan la operación de suma cuando las secuencias de bits de entrada son grandes. Pero aquí, dará la salida para cualquiera de las secuencias de bits de entrada con cierto retraso. Según los circuitos digitales, si el circuito da la salida con retardo no será preferible. Esto puede superarse con un circuito sumador de búsqueda de acarreo.
Si quieres conocer otros artículos parecidos a Sumador de arrastre de ondas : Funcionamiento, tipos y sus aplicaciones puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!