Qué es el Conversor de Códigos : Conversión de código binario a gris y de código gris a binario

En informática, necesitamos convertir binario a gris y gris a binario. Esta conversión puede realizarse mediante dos reglas: la conversión de binario a gris y la conversión de gris a binario. En la primera conversión, el MSB del código gris equivale constantemente al MSB del código binario. Los bits adicionales de la salida del código gris pueden llegar utilizando el concepto de puerta lógica EX-OR a los códigos binarios en ese índice actual así como en el índice anterior. Aquí el MSB no es más que el bit más significativo. En la primera conversión, el MSB del código binario equivale constantemente al MSB del código binario particular. Los bits adicionales de la salida del código binario se pueden obtener utilizando el concepto de puerta lógica EX-OR, verificando los códigos grises en ese índice actual. Si el bit de código gris actual es cero, entonces después se copia el código binario anterior, así como la copia inversa del bit de código binario anterior. Este artículo trata una visión general de los convertidores de código que incluye el convertidor de código binario a gris, así como el convertidor de código gris a binario.

¿Qué es un código binario?

En los ordenadores digitales, el código que se utiliza basado en un sistema numérico binario se conoce como código binario. Hay dos estados posibles como ON y OFF que se representan a través de 0 y 1. El sistema digital utiliza 10 dígitos donde cada posición de dígito significa la potencia de 10. En un sistema binario, cada posición de un dígito representa una potencia de 2.

Una señal de código binario incluye una secuencia de impulsos eléctricos que significan caracteres, números y operaciones a ejecutar. Se utiliza un dispositivo de reloj para transmitir los pulsos normales, así como componentes como los transistores, que se encienden/apagan para que fluyan o se bloqueen las señales. En el código binario, cada número decimal que va del 0 al 9 puede significarse mediante un conjunto de 4 bits/dígitos binarios. Las 4 operaciones aritméticas básicas, como la suma, la resta, la multiplicación y la división, pueden reducirse a combinaciones de funciones algebraicas booleanas básicas sobre números binarios.

¿Qué es el código gris?

El Código Gris o RBC (código binario reflejado), o código cíclico, es una serie de sistemas numéricos binarios. La razón principal para llamarlo código binario reflejado es que los N/2 valores iniciales están en orden inverso en comparación con los N/2 últimos valores. En este tipo de código, los dos valores sucesivos se cambian por un solo bit de dígitos binarios. Estos códigos se utilizan principalmente en las series comunes de números binarios generados por el hardware.

Los números binarios pueden dar lugar a errores una vez que se realiza la transición de un número único a uno consecutivo. Este tipo de código resuelve básicamente este problema alterando simplemente un bit una vez que se realiza el cambio entre los números.

Este tipo de código es extremadamente ligero y no depende del valor del dígito que se indica en la posición. Este tipo de código también se denomina código de variable cíclica porque el cambio de un valor único a su valor consecutivo supone el cambio de un solo bit.

Es el más popular para los códigos de distancia unitaria; sin embargo, no es apropiado para las funciones aritméticas. Las aplicaciones del código gris incluyen los convertidores analógicos a digitales y la comunicación digital para la corrección de errores. En primer lugar, el código gris no es fácil de entender, sin embargo, resulta muy fácil de reconocer.

Convertidor de código binario a gris

El código binario es una representación muy sencilla de los datos que utiliza dos valores, como 0 y 1, y se utiliza principalmente en el mundo de la informática. El código binario puede ser un valor alto (1) o bajo (0) o incluso un valor modificado. El código gris o código binario reflejado estima la naturaleza del código binario que se dispone con indicadores de encendido y apagado, normalmente denotados con unos y ceros. Estos códigos se utilizan para observar la claridad y la modificación de errores en las comunicaciones binarias.

La conversión de código binario a código gris puede realizarse mediante un circuito lógico. El código gris es un código no ponderado porque no se asigna un peso determinado a la posición del bit. Se puede obtener un código de n bits reproduciendo un código de n-1 bits en un eje posterior a las filas de 2^n-1, así como colocar el bit más significativo de 0 sobre el eje con el bit más significativo de 1 debajo del eje. A continuación se muestra la generación del código gris paso a paso.

Este método utiliza una puerta Ex-OR para actuar entre los bits binarios. El siguiente ejemplo será muy útil para conocer la conversión de binario a gris. En este método de conversión, anota el bit MSB del número binario actual, ya que el bit primario o MSB del número de código gris es similar al número binario.

Para obtener los bits de código gris rectos para generar el correspondiente dígito de código gris para los dígitos binarios dados, añade el dígito primario o el dígito MSB del número binario hacia el segundo dígito y anota el producto junto al bit primario del código gris, y añade el siguiente bit binario al tercer bit y anota el producto junto al 2^nd bit de código gris. Del mismo modo, sigue este procedimiento hasta el último bit binario y anota los resultados en función de la operación lógica EX-OR para generar el correspondiente dígito binario codificado en gris.

Ejemplo de convertidor de código binario a gris

Supongamos que los dígitos del código binario son bo, b1, b2, b3, mientras que el código gris concreto puede obtenerse a partir del siguiente concepto.

De la operación anterior, finalmente podemos obtener los valores de gris como g3 = b3, g2 = b3 XOR b2, g1= b2 XOR b1, g0 = b1 XOR b0.

Por ejemplo, toma el valor binario b3, b2, b1, b0 = 1101 y encuentra el código gris g3, g2, g1, g0 basándote en el concepto anterior

g3=b3=1

g2 = b3 XOR b2 = 1 XOR 1 =0

g1= b2 XOR b1= 1 XOR 0 = 1

g0= b1 XOR b0= 0 XOR 1 = 1

El código gris final para el valor del binario 1101 es 1011

Tabla de conversión de código binario a gris

Número decimal	Código binario	Código gris
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

Código VHDL para la conversión de código binario a gris se indica a continuación.

BIBLIOTECA ieee;
USE ieee.std_logic_1164.ALL;
la entidad bin2gray es
port( bin : en std_logic_vector(3 a 0); -entrada binaria
G : out std_logic_vector(3 a 0) -salida de código gris
);
fin bin2gray;
arquitectura gate_level de bin2gray es
empezar
-xor puertas.
G(3) <= bin(3);
G(2) <= bin(3) xor bin(2);
G(1) <= bin(2) xor bin(1);
G(0) <= bin(1) xor bin(0);
fin;

Ventajas

El ventajas del código binario incluyen las siguientes.

• La principal ventaja de utilizar el código binario es que se significa de forma sencilla a través de dispositivos electrónicos
• Los datos binarios también son muy fáciles de almacenar.
• Es muy fácil de significar y controlar electrónica y mecánicamente.
• Se puede aumentar la disparidad entre las representaciones de los símbolos para reducir la posibilidad de error.

El desventajas del código binario incluyen las siguientes.

• Se puede aumentar el número de símbolos necesarios para significar un número determinado de sistemas de valores de posición global.
• Los humanos no pueden leerlos de forma extremadamente eficaz debido a su longitud & y al uso de números de base diez por defecto
• Utiliza muchos dígitos para significar cualquier número lógico

Aplicaciones

Las aplicaciones del código binario son las siguientes

• Los códigos binarios se utilizan tanto en las telecomunicaciones como en la informática para diferentes técnicas de codificación de datos, como cadenas de caracteres a cadenas de bits. La anchura utilizada por estos métodos es fija, de lo contrario se trata de cadenas de anchura variable.
• Se utiliza en los lenguajes informáticos, así como en la programación, porque los lenguajes informáticos dependen principalmente de sistemas numéricos de 2 dígitos.

Convertidor de código gris a binario

Este método de conversión de gris a binario también utiliza el concepto de funcionamiento de la puerta lógica EX-OR entre los bits de gris y los bits binarios. El siguiente ejemplo con el procedimiento paso a paso puede ayudar a conocer el concepto de conversión de código gris a código binario.

Para cambiar el código gris a binario, anota el dígito MSB del número del código gris, ya que el dígito primario o el MSB del código gris es similar al dígito binario.

Para obtener el siguiente bit binario recto, utiliza la operación XOR entre el bit primario o MSB del binario al siguiente bit del código gris.

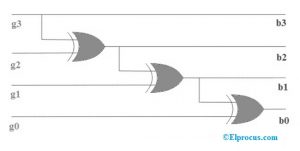
Del mismo modo, para obtener el tercer bit binario recto, utiliza la operación XOR entre el segundo bit o bit MSB del binario al tercer bit MSD del código gris y así sucesivamente.

Ejemplo de convertidor de código gris a binario

Supongamos que el Código Gray dígitos g3, g2, g1, g0 mientras que los dígitos particulares del código binario son bo, b1, b2, b3 se pueden obtener basándose en el siguiente concepto.

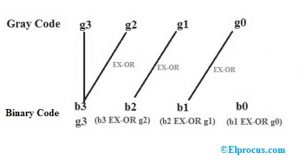
De la operación anterior, finalmente podemos obtener los valores binarios como b3 = g3, b2 = b3 XOR g2, b1= b2 XOR g1, b0 = b1 XOR g0.

Por ejemplo, toma el valor gris g3, g2, g1, g0 = 0011 y encuentra el código binario b3, b2, b1, b0 basándote en el concepto anterior

b3=g3=0

b2 = b3 XOR g2 = 0 XOR 0 =0

b1= b2 XOR g1= 0 XOR 1 = 1

b0= b1 XOR g0= 1 XOR 1 = 0

El código binario final para el valor del gris 0011 es 0010

Tabla de conversión de gris a código binario

Número decimal	Código gris	Código binario
0	0000	0000
1	0001	0001
2	0010	0010
3	0011	0011
4	0110	0100
5	0111	0101
6	0101	0110
7	0100	0111
8	1100	1000
9	1101	1001
10	1111	1010
11	1110	1011
12	1010	1100
13	1011	1101
14	1001	1110
15	1000	1111

Ventajas

El ventajas del código gris incluyen las siguientes.

• El circuito lógico puede reducirse
• Utilizado en el cruce del dominio del reloj
• Se utiliza para minimizar el error al cambiar las señales de analógicas a digitales
• Una vez que se utiliza dentro de los algoritmos genéticos, se puede reducir la aparición de la pared de martillo.

Desventajas

Las desventajas del código gris son las siguientes

• No es apropiado para las funciones aritméticas
• Aplicable para pocas aplicaciones precisas

Aplicaciones

Las aplicaciones del código gris son las siguientes

• Se utiliza en los convertidores analógico-digitales
• En la comunicación digital para corregir un error
• Reduce los errores al cambiar las señales de analógicas a digitales.
• Rompecabezas matemáticos
• Minimización de un circuito booleano
• Se utiliza para la comunicación entre dos dominios de reloj
• Algoritmos genéticos
• Codificadores de posición

Código VHDL para la conversión de código gris a binario se indica a continuación.

BIBLIOTECA ieee;
USE ieee.std_logic_1164.ALL;
la entidad gray2bin es
port( G : en std_logic_vector(3 a 0); -entrada de código gris
bin : out std_logic_vector(3 a 0) -salida binaria
);
fin gray2bin;
arquitectura gate_level de gray2bin es
comenzar
-xor puertas.
bin(3) <= G(3);
bin(2) <= G(3) xor G(2);
bin(1) <= G(3) xor G(2) xor G(1);
bin(0) <= G(3) xor G(2) xor G(1) xor G(0);
fin;

convertidor de código binario a gris de 3 bits

Supongamos que los dígitos binarios en un número binario de 3 bits son b0 , b1 , b2, donde el bit "b2" es el MSB (bit más significativo) y el bit "b0" es el LSB (bit menos significativo) del binario. Los dígitos del código Gray son g0, g1, g2, donde el dígito "g2" es el MSB (bit más significativo) mientras que el dígito "g0" es el LSB (bit menos significativo) del código Gray.

Código binario - b2,b1,b0	Código gris - g2,g1,g0
000	000
001	001
010	011
011	010
100	110
101	111
110	101
111	100

Así, la expresión booleana puede resolverse para el convertidor de código binario a gris utilizando el mapa k, podemos obtener g2 = b2, g1 = b1⊕ b2 y g0 = b0 ⊕ b1. Asimismo, podemos convertir un número binario de n bits (bnb (n-1) ...b2 b1 b0) en código gris ( gng (n-1) ...g2 g1 g0).

Para el LSB (bit menos significativo)

g0 = b0⊕b1

g1= b1⊕b2

g2 = b1⊕b2

g(n-1) = b (n-1) ⊕ bn, gn = bn.

Por ejemplo, convierte los números binarios 111010 en código Gray.

Entonces, basándonos en el algoritmo anterior

g0 = b0 ⊕ b1 => 0 ⊕ 1 = 1

g1=b1 ⊕ b2 = 1 ⊕ 0 = 1

g2 = b2 ⊕ b3 = 0 ⊕1 = 1

g3 = b3 ⊕ b4 = 1⊕1 = 0

g4 = b4 ⊕ b5 = 1 ⊕ 1 = 0

g5 = b5 = 1 = 1

Por lo tanto, la conversión del código binario a gris será - 100111.

Convertidor de código binario a gris con el IC 7486

La conversión de binario a gris y de gris a binario puede hacerse utilizando el IC7486. Los componentes necesarios para realizarlo son una protoboard, cables de conexión, LEDs, resistencias, XOR (IC7486), interruptores de botón y una batería para la alimentación.

El paquete del IC7486 incluye principalmente cuatro puertas lógicas XOR, donde los pines 7 y 14 proporcionarán la alimentación para todas las puertas lógicas. La o/ps de una sola puerta XOR se conecta a la entrada de la otra puerta lógica dentro del mismo u otro chip hasta que compartan un terminal de tierra similar.

Así pues, todo esto es sobre el convertidor de código binario a gris y el convertidor de código gris a binario. De la información anterior, finalmente, podemos concluir que estos convertidores desempeñan un papel esencial en la realización de diferentes operaciones de electrónica digital, así como en las comunicaciones entre varios sistemas numéricos. Los ejemplos de convertidores de código que hemos comentado anteriormente pueden ser útiles para comprender el concepto de cómo realizar estos cálculos. He aquí una pregunta para ti, ¿cuáles son las aplicaciones de los códigos grises?