Diferentes tipos de filtros Chebyshev con cálculos.

El nombre de los filtros Chebyshev lleva el nombre de "Pafnufy Chebyshev" porque sus características matemáticas se derivan solo de su nombre. Los filtros Chebyshev no son más que filtros analógicos o digitales. Estos filtros tienen una atenuación más pronunciada y un tipo de filtro 1 (más ondulación de banda de paso) o tipo de filtro 2 (ondulación de banda suprimida) que los filtros Butterworth. La propiedad de este filtro es que reduce el error entre la característica de filtro real e idealizada. Porque, inherente a la ondulación del ancho de banda en este filtro.

filtro Chebyshev

Los filtros Chebyshev se utilizan para distintas frecuencias de banda a banda. No pueden igualar el rendimiento del filtro del fregadero de la ventana y son adecuados para muchas aplicaciones. La característica principal del filtro Chebyshev es su velocidad, normalmente más rápida que el sinc con ventana. Porque estos filtros están hechos por recursión en lugar de por convolución. El diseño de los filtros Chebyshev y Windowed-Sinc depende de una técnica matemática llamada transformada Z.

Tipos de filtros Chebyshev

Los filtros Chebyshev se clasifican en dos tipos, a saber, filtro Chebyshev tipo I y filtro Chebyshev tipo II.

Filtros tipo I Chebyshev

Este tipo de filtro es el tipo básico del filtro Chebyshev. La respuesta de amplitud o ganancia es una función de frecuencia angular de orden n del LPF (filtro de paso bajo) es igual al valor total de la función de transferencia Hn (jw)

Gn(w)=|Hn (jω)|=1√(1+ϵ2Tn2() ω/ωo)

Donde,ε = factor de ondulación
ωo= frecuencia de corte
Tn= polinomio de Chebyshev de orden n

El ancho de banda muestra un rendimiento equivalente. En esta banda, el filtro cambia entre -1 y 1, por lo que la ganancia del filtro cambia entre máximo en G=1 y mínimo en G=1/√(1+ε2). En la frecuencia de corte, la ganancia es 1/√(1+ε2) y permanece para caer en la banda de parada cuando aumenta la frecuencia. El comportamiento del filtro se muestra a continuación. La frecuencia de corte de -3dB generalmente no se aplica a los filtros Chebyshev.

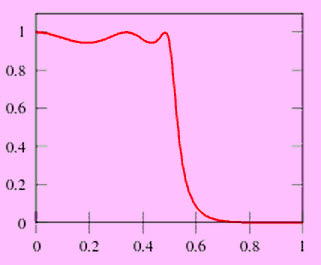
El orden de este filtro es similar al no. componentes reactivos necesarios para el filtro Chebyshev utilizando dispositivos analógicos. La ondulación en dB es 20log10 √(1+ε2). Entonces, la amplitud de una ondulación de 3db resulta de ε = 1. Se puede encontrar una caída aún más pronunciada si la ondulación se permite en la banda de parada, permitiendo 0 en el eje jw en el plano complejo. Sin embargo, este efecto en menos supresión en la banda de parada. El efecto se llama Cauer o filtro elíptico.

Polos y ceros del filtro Chebyshev tipo I

Los polos y ceros del filtro Chebyshev tipo 1 se analizan a continuación. Los polos del filtro Chebyshev se pueden determinar por la ganancia del filtro.

-js=cos(θ) & la definición trigonométrica del filtro se puede escribir

Aquí θ se puede resolver por

Donde los muchos valores de la función arco coseno se han aclarado utilizando el índice numérico m. Entonces las funciones del polo de ganancia de Chebyshev son

Usando las propiedades de las funciones hiperbólicas y trigonométricas, esto se puede escribir de la siguiente forma

La ecuación anterior produce los polos de la ganancia G. Para cada polo existe el complejo conjugado, y para cada par de conjugados existen otros dos negativos del par. La TF debe ser estable, La función de transferencia (TF) viene dada por

Filtro tipo II Chebyshev

Tipo II filtro Chebyshev También se conoce como filtro inverso, este tipo de filtro es menos común. Porque no rueda y necesita varios componentes. No tiene ondulación en la banda de paso, pero tiene ondulación equivalente en la banda de parada. La ganancia del filtro Chebyshev tipo II es

En la banda de parada, el polinomio de Chebyshev cambia entre -1 y 1, por lo que la ganancia 'G' cambiará entre cero y

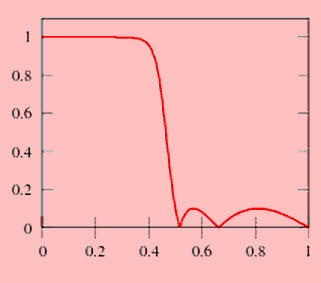
La frecuencia más pequeña a la que se alcanza este máximo es la frecuencia de corte.

Para una atenuación de banda suprimida de 5 dB, el valor de ε es 0,6801 y para una atenuación de banda suprimida de 10 dB, el valor de ε es 0,3333. La frecuencia de corte es f0 = ω0/2π0 y la frecuencia de 3dB fH se obtiene como

Polos y ceros del filtro Chebyshev tipo II

Supongamos que la frecuencia de corte es 1, los polos del filtro son los ceros del denominador de la ganancia

Los polos de ganancia del filtro Tipo II son polos opuestos del filtro Chebyshev Tipo I

Aquí en la ecuación anterior m = 1, 2, …, n. Los ceros del filtro de tipo II son ceros del numerador de ganancia

Los ceros del filtro de Chebyshev Tipo II son opuestos a los ceros del polinomio de Chebyshev.

Aquí, m = 1,2,3,………n

Usando un semiplano izquierdo, al TF se le da la función de ganancia y tiene ceros similares que son ceros simples en lugar de ceros dobles.

Entonces, estos son el filtro Chebyshev, los tipos de filtro Chebyshev, los polos y ceros del filtro Chebyshev y el cálculo de la función de transferencia. Esperamos que tenga una mejor comprensión de este concepto, además de cualquier consulta sobre este tema o proyectos electrónicos, dé su opinión comentando en la sección de comentarios a continuación. Aquí hay una pregunta para usted, ¿cuáles son las aplicaciones de los filtros Chebyshev?