Medición y Control de Potencia de RF (Parte I)
La figura 1 muestra una cadena de señales de comunicaciones moderna típica. La señal que se transmitirá se genera en la banda base mediante un convertidor de digital a analógico (DAC). Esta señal luego se mezcla en una frecuencia intermedia (IF) donde se filtra antes de mezclarse en la radiofrecuencia final (RF. ) En el lado de recepción tiene lugar la transformación inversa. La señal recibida se amplifica, se mezcla a IF y se filtra antes de mezclarla a banda base donde se digitaliza.
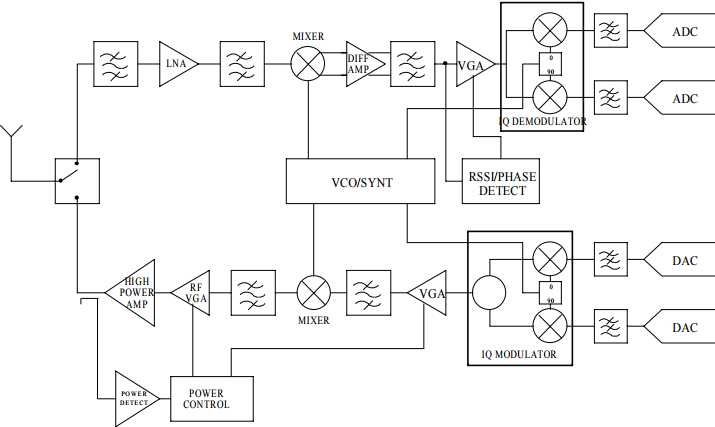
Fig. 1: Una cadena de señal de RF moderna
Si bien las cadenas de señales como estas vienen en todas las formas y tamaños, existe una necesidad universal en las aplicaciones de comunicaciones para medir y controlar la potencia de la señal. En el lado de la transmisión, debemos asegurarnos de que el amplificador de potencia (PA) cumpla con los requisitos reglamentarios de emisiones. También debemos asegurarnos de que el PA no esté transmitiendo por encima de un nivel de potencia que pueda dañarlo por sobrecalentamiento.
En el lado de la recepción, el nivel de la señal de entrada generalmente variará en algún rango dinámico. Esto puede deberse a las condiciones meteorológicas o a que la fuente de la señal recibida se aleja del receptor (p. ej., un teléfono móvil que funciona en un automóvil rápido). En general, queremos presentar un nivel de señal constante a la señal analógica a convertidor digital (ADC), ya que esto maximizará la relación señal-ruido (SNR). Para hacer esto, las cadenas de señales de recepción suelen utilizar uno o más amplificadores de ganancia variable (VGA) que están controlados por dispositivos de medición de potencia que completan el control automático de ganancia. (AGC) bucle. Tenga en cuenta que, si bien el control de potencia de transmisión puede ocurrir en RF o en FI, el procesamiento de la señal del lado de recepción generalmente se realiza en FI.
En ambos casos, la precisión de la medición de la intensidad de la señal puede ser crítica. Por ejemplo, considere una estación base que transmite una potencia promedio de +50 dBm (100 W). Si el detector que regula la potencia transmitida desde la estación base tiene un error impredecible sobre la temperatura de ±3 dB, es posible que la base la estación puede en algún momento ser dirigida a transmitir 53 dBm (200 W). Esto es claramente inaceptable ya que agregaría un costo excesivo al dimensionamiento térmico adicional de la unidad.
En el lado de la recepción, un circuito de medición impreciso dará como resultado una mala nivelación de la señal que se presenta al ADC. Esto sobrecargará el ADC (señal de entrada demasiado grande) o desperdiciará un rango dinámico valioso (señal de entrada demasiado pequeña).
Esta serie trata muchos de los problemas asociados con la medición y el control de los niveles de potencia de RF. Se examinarán diversas técnicas de medición de potencia, como diodos, térmicas, rms a CC y log amperios. También se examinarán cuestiones como el tiempo de respuesta, el rango dinámico, la resolución, el factor de cresta variable, la estabilidad de la temperatura, el tamaño y el costo.
Energía
La potencia en vatios se puede expresar de varias maneras, es decir
donde V es el voltaje rms, I es la corriente rms y R es la resistencia en la que se disipa la potencia. Dado que la mayoría de los sistemas de comunicaciones tienen impedancias constantes de carga y fuente, por lo general de 50 Ω, se deduce que solo necesitamos conocer el voltaje rms para calcular la potencia. Como resultado, muchos circuitos prácticos de medición de potencia dependen de la medición del voltaje rms.
Conversión entre dBm, dBmV, W, RMS y voltaje de pico a pico
Los niveles de señal en aplicaciones de comunicaciones por cable generalmente se especifican en dBm. Sin embargo, para aquellos detectores de "potencia" que responden al voltaje, realmente deberíamos especificar el voltaje de salida con respecto a su entrada Voltaje. Esto puede ser bastante confuso para las personas que viven en un mundo dB. El asunto se complica aún más por la respuesta cambiante de muchos detectores en presencia de una relación pico a promedio cambiante en la señal de entrada.
La unidad dBm se define como el nivel de potencia en dB referenciado a 1 mW, es decir
donde la potencia se especifica en vatios.
Dado que la potencia en vatios es igual al voltaje rms al cuadrado, dividido por la impedancia, también podemos escribir esto como
De ello se deduce que 0 dBm es igual a 1 mW, +10 dBm es igual a 10 mW, +30 dBm es igual a 1 W, etc. Debido a que la impedancia es un componente de esta ecuación, generalmente deberíamos especificar la impedancia de línea cuando hablamos de dBm niveles (por ejemplo, 20 dBm: Re 50 Ω.)
La unidad dBV se define como el nivel de voltaje, en dB, referenciado a 1 Vrms, es decir
Por lo tanto, 0 dBV es igual a 1 Vrms. La Fig. 2 muestra cómo se relacionan entre sí los voltios rms, los voltios pico a pico, dBV, dBm y mW. Sin embargo, esto solo es válido para una impedancia de carga de 50 y un factor de cresta de 1,4142 (es decir, una onda sinusoidal donde Vrms = Vpico-pico/2/1,4142). Tenga en cuenta que en un sistema de 50, existe una compensación constante de 13 dB entre dBV y dBm (dBm = dBV + 13.)

Fig. 2: Conversión entre potencia y voltaje
Definición de RMS1
RMS (o raíz cuadrada media) es una medida fundamental de la magnitud de una señal de CA. Su definición puede ser tanto práctica como matemática. Definido de manera práctica: el valor rms asignado a una señal de CA es la cantidad de CC requerida para producir una cantidad equivalente de calor en la misma carga. Por ejemplo, una señal de CA de 1 Vrms producirá la misma cantidad de calor en una resistencia que una señal de 1 VCC. Definido matemáticamente, el valor rms de un voltaje es,
Esto implica elevar al cuadrado la señal, tomar el promedio y obtener la raíz cuadrada. El tiempo promedio debe ser lo suficientemente largo para permitir el filtrado a las frecuencias más bajas de operación deseadas.
Definición de factor de cresta
El factor de cresta de una forma de onda es la relación entre su valor máximo y su valor rms. Las señales como las ondas cuadradas de amplitud simétrica o los niveles de CC tienen un factor de cresta de uno. Otras formas de onda, de naturaleza más compleja, tienen factores de cresta más altos. Una onda sinusoidal tiene un factor de cresta de 2 (es decir, 1,4142). Por lo tanto, una onda sinusoidal con un nivel rms de 1 V tiene una amplitud de pico a pico de 2,8284 V).
Técnicas de medición de la magnitud de la señal
I Detección de diodos
La figura 3 muestra el esquema de un circuito de detección de diodo popular. Este es un rectificador simple de media onda con filtrado de salida. Una resistencia de 68 en la entrada crea una coincidencia de entrada nominal de 50.

Fig. 3: Un detector de diodo simple 2
La Fig. 4 muestra el voltaje de salida en función de la señal de entrada en dBm.

Fig. 4: Vs vs. Pin para un circuito detector de diodo simple
Si bien la función de transferencia de este circuito a 25 °C es razonablemente lineal, el rendimiento se degrada significativamente a niveles de entrada bajos y sobretemperatura. La figura 5 muestra un circuito detector de diodo modificado que incorpora alguna compensación de temperatura. En este circuito, la dependencia de la temperatura del voltaje del diodo se compensa con un segundo diodo. Entonces, a medida que la caída de voltaje en D1 aumenta con la temperatura, se mantiene un voltaje idéntico en D2. Esto mantiene constante el voltaje en el centro del divisor de resistencia, que se usa como salida.

Fig. 5: Detector de diodo con compensación de temperatura 2

Fig. 6: Vout y Error vs. Pin para un detector de diodo con compensación de temperatura
La Fig. 6 muestra la función de transferencia de este circuito con compensación de temperatura. Para observar más de cerca la linealidad mejorada y la estabilidad de la temperatura, la regresión lineal puede calcular el mejor ajuste en línea recta para estos puntos; es decir, una ecuación con la forma,
Tenga en cuenta que para hacer este cálculo, es necesario convertir los números de potencia en dBm a voltaje (una función de transferencia de voltaje de entrada/salida da una relación nominalmente lineal). Usando esta línea recta ideal, podemos trazar la linealidad de la respuesta sobre su rango dinámico. En aplicaciones prácticas, nos gustaría calibrar el circuito a temperatura ambiente pero no a temperatura excesiva. Por tanto calculamos el error sobre la temperatura con respecto a la mejor recta, medida a temperatura ambiente. Esto nos da una buena medida de la precisión a nivel de sistema de esta solución.
La Fig. 6 muestra que el detector de diodo con compensación de temperatura tiene una buena estabilidad de temperatura a niveles de potencia altos, pero aún se vuelve menos estable a la temperatura y menos lineal a niveles de entrada bajos. Es importante tener en cuenta que la salida del circuito no se puede cargar con ninguna resistencia significativa. A bajas temperaturas, este circuito tiene una impedancia de salida extremadamente alta. De hecho, manejar cualquier cosa menos que un amplificador de búfer FET dará como resultado que el algoritmo de compensación de temperatura falle, brindando un rendimiento similar al de la Fig. 4.
Los circuitos detectores de diodo no miden la fuerza de la señal de verdadero valor eficaz, y el voltaje de salida de estos detectores cambia en función del factor de cresta de la señal de entrada, incluso cuando la fuerza de la señal de entrada permanece constante (un factor de cresta más alto da un voltaje de salida más bajo). Sin embargo, en un sistema donde las señales tienen un factor de cresta constante, esto puede no importar siempre que el detector se haya calibrado correctamente. Entonces, si un enlace de radio, por ejemplo, usa solo un esquema de modulación (por ejemplo, QPSK), se pueden realizar mediciones de potencia precisas. Sin embargo, en sistemas con factores de cresta variables, como CDMA o WCDMA, las mediciones de verdadero valor eficaz se vuelven difíciles. Una solución a este problema es usar diferentes tablas de búsqueda basadas en la carga de llamadas en la estación base (es la carga de llamadas en un canal particular lo que altera el factor de cresta). Sin embargo, esto requiere la calibración de la estación base para cada escenario de carga de llamadas. El problema empeora aún más en los sistemas de múltiples portadoras donde el factor de cresta de múltiples portadoras cambia independientemente unas de otras.
II Detección Térmica
La detección térmica implica esencialmente la implementación práctica de la definición clásica de rms que vimos anteriormente. Esta es la técnica de medición de verdadero valor eficaz más simple en teoría; sin embargo, en la práctica es difícil y costoso de implementar. Implica comparar el valor calorífico de una señal de CA desconocida con el valor calorífico de un voltaje de referencia de CC calibrado conocido (consulte la Fig. 7). Cuando el voltaje de referencia calibrado se ajusta para anular la diferencia de temperatura entre la resistencia de referencia (R2) y el resistencia de señal (R1), la potencia disipada en estas dos resistencias emparejadas será igual. Por lo tanto, según la definición básica de rms, el valor del voltaje de referencia de CC será igual al valor rms del voltaje de señal desconocido.

Fig. 7: Detección térmica
Cada unidad térmica contiene una resistencia estable de bajo TC (R1, R2) que está en contacto térmico con un convertidor lineal de temperatura a voltaje (S1, S2), un ejemplo del cual sería un termopar. El voltaje de salida de S1/S2 varía en proporción al cuadrado medio de Vin; la relación temperatura/voltaje de primer orden variará como K Vin/R1.
El circuito de la Fig. 7 normalmente tiene un error muy bajo (aproximadamente 0,1 %), así como un ancho de banda amplio. Sin embargo, la constante de tiempo fija de la unidad térmica (R1S1, R2S2) limita la efectividad de baja frecuencia de este esquema computacional rms.
Además de este tipo básico, también hay disponibles convertidores térmicos de ganancia variable que pueden superar las limitaciones del rango dinámico de los convertidores de ganancia fija a expensas de una mayor complejidad y costo.
[Part II of this series will introduce log amps and detail how they can be used in control loops.]
Referencias
Un detector de potencia armónica suprimida para teléfonos de doble bandaA Rixon y R Waug
Si quieres conocer otros artículos parecidos a Medición y Control de Potencia de RF (Parte I) puedes visitar la categoría Generalidades.
Deja una respuesta

¡Más Contenido!