Esta sección describe brevemente los problemas relacionados con las líneas de transmisión en las redes eléctricas. El conocimiento de los equipos aquí descritos es de gran utilidad para el personal técnico en electricidad, su producción y distribución.
Efecto inductivo y capacitivo
Además de la resistencia óhmica en cables y conductores eléctricos, los conductores que transportan corriente alterna tienen efectos inductivos y capacitivos.
Considere, por ejemplo, un par de líneas de transmisión que se extienden por varios kilómetros y compárelas con dos placas que forman un capacitor. Verás que hay una similitud en las dos superficies metálicas, al estar muy separadas, con un área común compartida separada por un material no conductor (aire). Así, los dos conductores forman un condensador.
Lo mismo ocurre con el efecto magnético de la corriente en cada conductor sobre sí mismo y sobre el otro conductor. Por lo tanto, hay una inductancia entre los dos conductores.
La magnitud de los efectos capacitivos e inductivos puede ser pequeña e insignificante para cables cortos, por ejemplo, en cableado doméstico de bajo voltaje, pero no son insignificantes para líneas de transmisión muy largas y los altos voltajes que transportan.
Por lo tanto, los efectos capacitivos e inductivos de las líneas de transmisión deben tenerse en cuenta al calcular su corriente y caída de tensión. Si se agregan estos efectos, la representación esquemática de una red eléctrica entre carga(s) y fuente(s) se verá como Figura 1ben vez de Figura 1a.
Los resistores y los inductores están en serie entre sí a lo largo de un conductor, pero los efectos capacitivos se muestran en paralelo. Estos efectos se muestran para una línea, pero corresponden a ambos conductores.
En la práctica, generalmente hay más de dos conductores, especialmente para líneas trifásicas. Pero, en el caso de un sistema trifásico, los efectos de dos conductores no son los mismos que en el caso de cables monofásicos porque no hay líneas de retorno que transporten las mismas corrientes al mismo tiempo.
Figura 1 Una ilustración típica de una línea de transmisión. (a) Dos cables de transmisión largos para corriente alterna. (b) Capacitores e inductores que muestran los efectos de la capacitancia y la inductancia de los cables adyacentes en la transmisión de CA.
Los valores de resistencia óhmica se pueden configurar fácilmente para cada conductor en función de su longitud, sección transversal, material del conductor y resistencia específica. Estos datos generalmente están disponibles para cualquier cable en términos de resistencia por cada metro de conductor, o 1000 pies del mismo.
Sin embargo, el valor del capacitor y el valor de la inductancia para una serie de conductores dependen de factores exclusivos de su configuración. Dependiendo de la separación de los conductores, sus lazos, cómo están dispuestos, el número de conductores y el número de haces que comparten la misma corriente, se puede determinar un valor para la inductancia de una longitud determinada (por ejemplo, 1 km o 1 milla) de línea de transmisión.
De manera similar, se puede encontrar un valor para la capacitancia. De esta forma, valores más precisos de corriente, caída de tensión, energía perdida, etc. encontrado para una línea de transmisión de una longitud dada.
efecto coronario
Otro fenómeno que provoca pérdidas en las líneas de transmisión es el corona. Corona es el efecto de la diferencia de potencial (voltaje) en el aire que rodea las líneas de transmisión, ionizando el aire. Este efecto se muestra en forma de un resplandor que sale de las líneas.
Corona depende del voltaje y el espacio entre los cables. Sin embargo, la cantidad de energía que se pierde es pequeña y, a menudo, se pasa por alto.
Corona: Corona es una descarga eléctrica localizada alrededor de los conductores de las líneas de transmisión de alto voltaje cuando el aire (especialmente húmedo) está ionizado. Se muestra como un brillo azulado y una ligera ictericia. Este fenómeno va acompañado de una pequeña pérdida de potencia utilizada para hacer sonar y brillar.
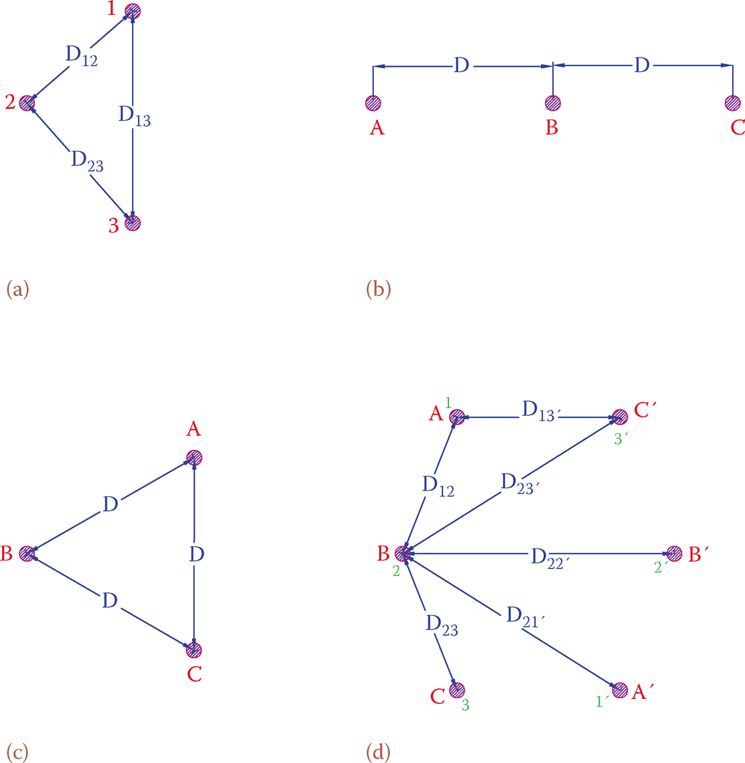
Figura 2 muestra el espaciamiento relativo entre posibles arreglos de líneas de transmisión. Figura 2a muestra una situación general en la que las tres líneas de un sistema trifásico están en las ubicaciones 1, 2 y 3. Además, estas líneas están separadas por distancias generales D12, D13 y D23.
En las siguientes discusiones, se supone que las cargas en las tres fases son las mismas y estamos tratando con cargas balanceadas. Excepto en caso Figura 2c donde todas las líneas están separadas por la misma distancia, los valores de inductancia y capacitancia no son iguales a la longitud de las líneas. Como resultado, las caídas de voltaje en las tres líneas son diferentes. Por lo tanto, en la ubicación de la carga, los voltajes en las tres líneas que transportan las tres fases no son los mismos. Además, las relaciones de fase pueden interrumpirse y las tres fases ya no estarán separadas 120°.
Figura 2 Ubicaciones de conductores en algunas líneas de transmisión trifásicas comunes. (a) En las tres esquinas de un triángulo. (b) a lo largo de una línea horizontal. (c) En las tres esquinas de un triángulo equilátero. (d) Doble circuito trifásico, tales como obras de transmisión.
Es altamente indeseable si los voltajes que llegan a un lugar desde la misma fuente son diferentes y no se proporciona un sistema trifásico adecuado al final de la línea.
efecto cruzado
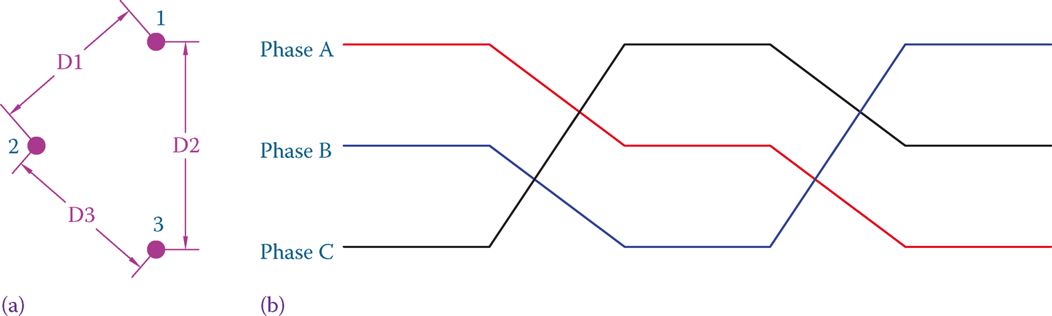
En muchos arreglos de líneas de transmisión no es común, y a veces es imposible, que las líneas estén en las esquinas de un triángulo equilátero (p. ej., Figura 2b y D). Para superar este problema, es común rotar las líneas, de modo que cada una de las fases tenga la misma posición física a lo largo de la línea de transmisión. De esta forma, se igualarán la inductancia y la capacitancia totales de las tres líneas. Esta rotación se llama transposicióny se dice que una linea esta tan manejada transpuesto. Esto se muestra en Figura 3, lo que muestra que cada una de las líneas trifásicas A, B y C se coloca igualmente en las tres ubicaciones físicas designadas por 1, 2 y 3 a lo largo de la línea de transmisión.
Cuando las tres fases de una línea ocupan las tres posiciones por igual, de modo que todas las diferencias de voltaje se anulan entre sí, se dice que la línea está totalmente transpuesta.
imagen 3 Transposición en líneas de transmisión. (a) Ubicación física de líneas trifásicas. (b) Intercambie las posiciones de los alambres en algún punto a lo largo de la línea.
Transposición: una disposición especial en la transmisión de energía trifásica, en la que los cables se giran de modo que la posición de los cables para cada fase se invierta físicamente de modo que cada cable esté en la misma posición que los otros cables a lo largo de la línea.
En lo que sigue asumimos que las líneas continuas son circulares y todas tienen el mismo radio r. Las longitudes D se definen con uno o dos subíndices si es necesario (como en D12).
Los números calculados son para la inductancia y la capacitancia para una longitud determinada y, por lo tanto, deben multiplicarse por la longitud de la línea de transmisión por la longitud total de la línea de transmisión. Los resultados de los cálculos son por fase para líneas trifásicas.
En los sistemas de un solo paso, los números de la inductancia deben duplicarse y la capacitancia debe reducirse a la mitad, ya que hay dos líneas y una es el retorno de la otra línea.
Antes de continuar, necesitamos definir los siguientes dos términos. De hecho, son los parámetros los que cambian, de un diseño de línea a otro.
La distancia media geométrica (GMD) es un número que corresponde a la misma distancia entre dos o más líneas (cables). El Radio Medio Geométrico (GMR) es un número que corresponde al radio efectivo de una o más líneas.
Distancia Geométrica (GMD): Término en las líneas de transmisión de energía que corresponde al espacio entre dos (en una fase) y tres o seis (en tres fases) líneas eléctricas utilizadas para determinar la inductancia y la capacitancia asociadas con las líneas.
Radio medio geométrico (RMG): Término en líneas de transmisión de energía que corresponde al tamaño (radio) de las líneas de energía utilizadas para determinar la inductancia y la capacitancia asociadas con ellas.
línea de estrangulamiento
La siguiente fórmula general se puede utilizar para encontrar la inductancia de cada línea en un sistema de transmisión. Si hay tres fases, se supone que la línea está transpuesta y la(s) carga(s) balanceada(s).
$begin{matriz}L=left( 2times {{10}^{-7}} right)ln left( frac{GMD}{GMR} right) & {} & left( 1right) end{matriz}$
GMD y GMR son como se definen anteriormente y varían según el caso. El coeficiente (2 × 10−7) para el sistema métrico, y la respuesta es henrys por metro. Para el sistema imperial es necesaria la conversión, como se verá más adelante en varios ejemplos. Consideramos GMD y GMR para los siguientes tres casos:
Logaritmo de un número
El uso de logaritmos es una herramienta útil en muchas ingenierías y otros campos. Facilita los cálculos y la resolución de problemas. Aquí explicamos brevemente qué es un logaritmo y mostramos algunos ejemplos.
Hay dos logaritmos, y podemos decir que cualquier número positivo tiene dos valores logarítmicos. El número base es la diferencia entre ellos, y es posible convertir de un logaritmo a otro.
Los dos logaritmos son el logaritmo decimal, que tiene una base de 10, y el logaritmo natural, que tiene un número de base diferente. Primero empezamos con el logaritmo decimal, y cuando lo entendemos bien, el otro es fácil de entender. De hecho, el logaritmo es lo opuesto a la potencia exponencial.
logaritmo decimal
Para mostrar el logaritmo decimal de un número se utiliza el símbolo "log", por ejemplo log 10, log 20, etc. Considere las siguientes relaciones. Puedes comprobarlos en una calculadora:
Junto con la relación anterior y en el mismo orden, puedes escribir
De los ejemplos anteriores es claro que si y = 10Xentonces x = log y.
Ahora que tiene claro el concepto de la función logarítmica, pruebe con números negativos para x y vea el resultado para y. Todos los valores obtenidos de esta forma son inferiores a 1,0. También recuerda que los números negativos no son logarítmicos. Recibirá un mensaje de error si intenta encontrar el registro de un número negativo en la calculadora.
Ahora consideramos GMD y GMR para los siguientes tres casos:
- caso monofásico (dos líneas)
[begin{align}& GMDtext{ }=text{ }D=text{ }thetext{ }distancetext{ }betweentext{ }thetext{ }lines & & GMR=r’=frac{r}{{{e}^{{}^{1}/{}_{4}}}}=0.7788r end{align}]
donde r es el radio del alambre. Como en este caso la línea de retorno tiene las mismas características y corriente que la línea principal, el valor obtenido para L debe duplicarse para representar el lazo cerrado.
Para líneas monofásicas, los valores calculados para la inductancia de la ecuación 1 deben duplicarse.
2. Caso de línea trifásica de un solo circuito (Figura 2a, b y c):
[begin{matrix}GMD=sqrt[3]{{{D}_{12}}times {{D}_{13}}times {{D}_{23}}} & {} & left( 2 right) {} & { } & {} GMR=frac{r}{{{e}^{{}^{1}/{}_{4}}}}=0.7788r & {} & left( 3 right) fin{matriz}]
(d12D13y D23 las distancias entre las líneas dadas i Figura 2r es el radio de los cables).
3. Caso de líneas trifásicas de doble circuito (Figura 2d):
Observe cómo se asignan números y letras a las líneas trifásicas y cómo se definen las diferentes longitudes.
[begin{matrix}GMD=sqrt[3]{{{D}_{A{{B}_{eq}}}}veces {{D}_{A{{C}_{eq}}}}}veces {{D}_{B{ { C}_{eq}}}}} & {} & left( 4 right) end{matriz}]
Dónde
[{{D}_{AB}}_{_{eq}}=sqrt[4]{{{D}_{12}}veces {{D}_{12′}}veces {{D}_{1'2}}veces {{D}_{1'2′}}} ]
[{{D}_{AC}}_{_{eq}}=sqrt[4]{{{D}_{13}}veces {{D}_{13′}}veces {{D}_{1'3}}veces {{D}_{1'3′}}} ]
[{{D}_{BC}}_{_{eq}}=sqrt[4]{{{D}_{23}}hora {{D}_{23'}}hora {{D}_{2'3}}hora {{D}_{2'3'}}} ]
Y
[begin{matrix}GMR=sqrt[3]{GM{{R}_{A}}times GM{{R}_{B}}times GM{{R}_{C}}} & {} & left( 5 right) terminar {editar}]
Dónde
$begin{matriz}GM{{R}_{A}}=sqrt{frac{R}{{{e}^{{}^{1}/{}_{4}}}}left ( {{D}_{11′}} right)} & {} & {} GM{{R}_{B}}=sqrt{frac{R}{{{e}^{{ }^{1}/{}_{4}}}}left( {{D}_{22′}} right)} & {} & left( 6 right) GM{{R} _{C}}=sqrt{frac{R}{{{e}^{{}^{1}/{}_{4}}}}left( {{D}_{33′}} right)} & {} & {} end{matriz}$
Los valores obtenidos de la relación anterior determinan la inductancia de cada línea de un sistema trifásico. Los valores están en Henrys por metro.
Tenga en cuenta que
$frac{1}{{{e}^{{}^{1}/{}_{4}}}}=frac{1}{{{e}^{0,25}}}=0,7788$
Por lo tanto, en todas las ecuaciones anteriores, este valor se puede usar directamente (e = 2.7183)
Una vez que se determina L, la reactancia inductiva de la línea se determina a partir de la relación conocida XL = 2πfL.
(Para cualquier definición entre líneas, consulte Figura 2d; se supone que cada línea tiene el mismo tamaño que el radio r).
Valores obtenidos para L y XL que es por metro de cada línea. Para la reactancia inductiva e inductiva de toda la línea, se deben multiplicar por la longitud de la línea.
recurso en línea
La capacitancia de línea de los conductores eléctricos se puede encontrar de la misma manera que sus inductores para varias disposiciones de línea. La única diferencia es el valor del radio medio geométrico, en lo que respecta a las fórmulas.
Además, un efecto de tierra entra en juego para la habilidad. Sin embargo, este efecto es solo una pequeña fracción de los valores de capacitancia debido a los propios cables y puede ignorarse si los cables no están muy cerca de tierra.
El valor de GMR para el caso es la capacitancia radial real del conductor. En este sentido, para cada cálculo de capacidad, el término $frac{1}{{{e}^{{}^{1}/{}_{4}}}}=frac{1}{{{ e } ^{0.25}}}=0.7788$ (cuando se ve en las ecuaciones de inductancia) debe reemplazarse por 1. La fórmula general para la capacitancia de los conductores en el sistema métrico es F/m y la respuesta se obtiene de la siguiente manera (faradios por metro). Para cualquier longitud de conductores, este valor debe multiplicarse por la longitud.
[begin{matrix}C=frac{2pi times 8.854times {{10}^{-12}}}{ln left( frac{GMD}{GMR} right)} & {} & left( 7 right) end{matrix}]
Para el caso simple de dos cables, GMR es simplemente el radio de los cables y GMD es su longitud. Los siguientes ejemplos determinan la capacitancia para algunos de los mismos conductores vistos anteriormente en esta sección.
El valor obtenido de Ecuación 7 la capacitancia entre cada línea de fase y neutro en un sistema trifásico balanceado. Para una fase, el valor calculado debe dividirse por 2 para obtener la capacitancia entre la línea directa y el neutro. En la ecuación anterior, se supone que el efecto arcilla es pequeño y no se incluye.
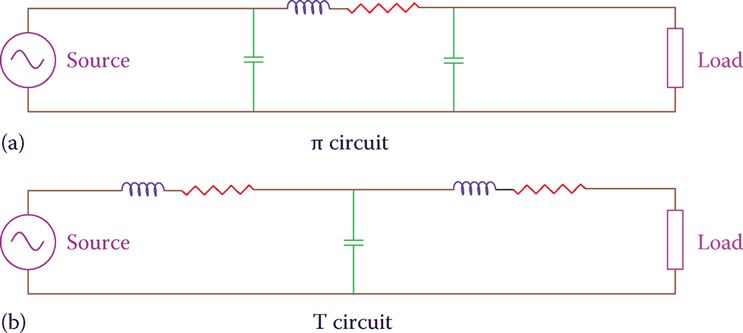
En la práctica, para líneas de longitud media (típicamente 80-250 km, 50-156 mi) después de encontrar los valores de resistencia, reactancia inductiva y reactancia capacitiva, la línea se modela como un circuito π o un circuito T, como se muestra en Figura 4.
En el modelo de circuito π, la capacitancia de cada capacitor es la mitad del valor total calculado. De manera similar, en el circuito T, los valores de las impedancias son la mitad del valor calculado.
Figura 4 Modelado de líneas de transmisión. (a) modelo π. (b) Modelo T.


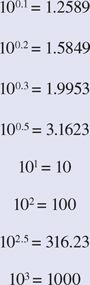
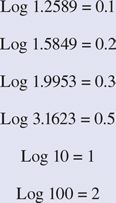
¡Más Contenido!