Teorema de transferencia de potencia máxima explicado con ejemplos

En cualquier circuito eléctrico y electrónico, la potencia se utiliza para entregar energía eléctrica a la carga dondequiera que se transforme en trabajo funcional. Básicamente, toda la fuente de alimentación no se cargará debido al efecto de calentamiento, así como a otras restricciones en el circuito. Por lo tanto, hay una cierta diferencia entre extraer y entregar poderes. El tamaño de la carga afectará la cantidad de energía entregada por la fuente de energía, cualquier cambio en la resistencia de la carga puede causar un cambio en la transferencia de energía a la carga. Así, el teorema de transferencia de máxima potencia o MPTT asegura la condición de entregar la máxima potencia a la carga.

En todas las aplicaciones electrónicas o eléctricas, la suma de las potencias obtenidas a través de una carga es un parámetro esencial. Por ejemplo, la carga en los circuitos de CC se puede representar mediante una resistencia con una resistencia de ohmios 'RL'. De manera similar, en los circuitos de CA, se puede indicar a través de una carga compleja de ohmios de impedancia 'ZL'. Este artículo presenta una descripción general de MPPT (Teorema de transferencia de potencia máxima).

¿Qué es el teorema de máxima transferencia de potencia?

los Teorema de transferencia de potencia máxima se puede definir como una carga resistiva conectada a una red de CC, cuando la resistencia de la carga (R_L) es equivalente a la resistencia interna ya que recibe la potencia más alta se conoce como resistencia equivalente de Thevenin de la red fuente. El teorema define cómo seleccionar la resistencia de carga (RL) cuando la fuente de resistencia se da una vez. Es un malentendido general aplicar el teorema en la situación inversa.

No significa que cómo seleccionar la fuente de resistencia para una resistencia de carga específica (RL). De hecho, la resistencia de la fuente que mejor aprovecha la transferencia de energía es constantemente cero, a excepción del valor de la resistencia de carga. Este teorema se puede extender a circuitos AC que incluyen una reactancia y define que la mayor transmisión de potencia ocurre cuando la impedancia de carga (ZL) debe ser equivalente a la ZTH (complejo conjugado de la impedancia del circuito correspondiente).

Teorema de Transferencia de Potencia Máxima Problemas Resueltos

1). Encuentre la resistencia de carga RL que permite que el circuito (a la izquierda de las terminales a y b) suministre la máxima potencia a la carga. También encuentre la potencia máxima entregada a la carga.

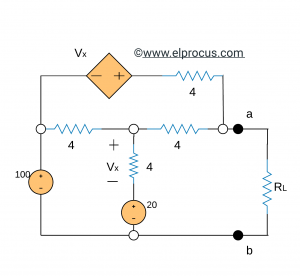
La solución:

Para aplicar el teorema de máxima transferencia de potencia, necesitamos encontrar el circuito equivalente de Thevenin.

(a) Rama V del circuito: voltaje de circuito abierto

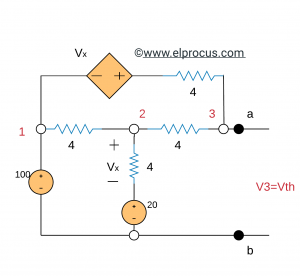
Restricciones: V1=100, V2 – 20=Vx y V3=Vth

En el nodo 2:

En el nodo 3:

(1)*2 + (2)*3 –> Vth=120 [V]

(b) Derivación Rth (por método de tensión de prueba): después de la desactivación y aplicación de la tensión de prueba, tenemos:

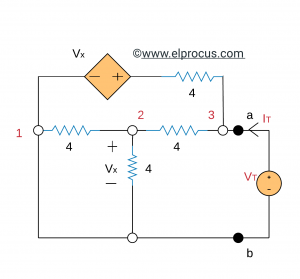
Restricciones: V3=VT y V2=Vx

En el nodo 2:

En el nodo 3 (KCL):

De (1) y (2):

(c) Máxima transferencia de potencia: ahora el circuito se reduce a:

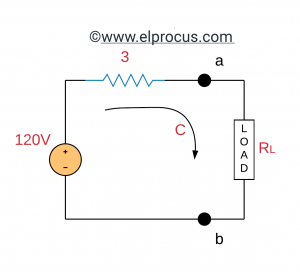
Para obtener la máxima transferencia de potencia, entonces, RL=3=Rth. Finalmente, la potencia máxima transferida a RL es:

2). Determine la potencia máxima que se puede entregar a la resistencia variable R.

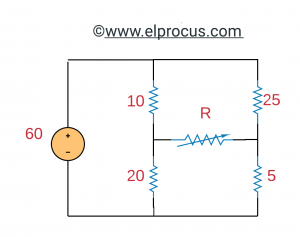
La solución:

(a) Vth: voltaje de circuito abierto

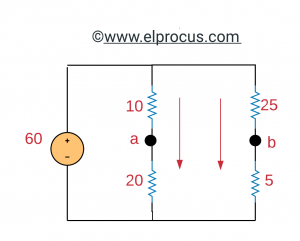
Del circuito, Vab=Vth=40-10=30 [V]

(b) Rth: aplique el método de resistencia de entrada:

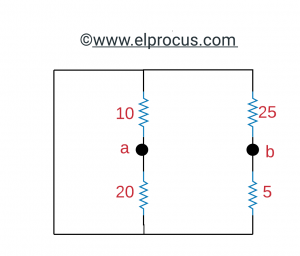
Entonces Rab= (10//20) + (25//5) = 6.67+4.16=10.83 =Rth.

(c) Circuito de Thévenin:

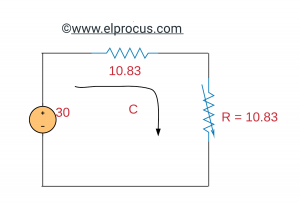
Fórmula MPTT

los Fórmula del teorema de transferencia de potencia máxima se explica a continuación. Considerando el η (eficiencia) como la fracción de potencia disuelta a través de la carga R a la potencia extendida en la fuente, HTVentonces es simple de calcular máxima eficiencia de transferencia de potencia como

η = (Pmáx/P) X 100 = 50 %

Dónde; la potencia máxima (Pmax)

Pmáx = V²_mi R_{mi / (}R_TH+ R_mi)2 ₌ V²_{mi /} 4R_mi

Y la potencia suministrada (P) es

P=2V²_{mi /} 4R_mi =V²_mi / 2R_mi

El η es solo del 50% cuando se alcanza la mayor transferencia de potencia, aunque llega al 100% cuando el R_L (resistencia de carga) alcanza el infinito, mientras que toda la etapa de potencia tiende a cero.

Teorema de transferencia de potencia máxima para circuitos de CA

En un circuito de CA, el MPTT proporciona las condiciones de impedancia para transferir la potencia más alta a una carga. Este teorema establece que en un circuito AC activo, se incluye una fuente a través de una impedancia interna como ZS que está conectada a una carga como ZL. Por lo tanto, la transferencia de potencia máxima ocurre principalmente desde la fuente a la carga una vez que la impedancia de carga es equivalente al conjugado compuesto de ZS o impedancia de fuente.

Como un arreglo inactivo, la potencia más alta pasa a la carga mientras que la impedancia de la carga es equivalente al complejo conjugado de una impedancia correspondiente de un arreglo dado como se observa a través de las terminales de carga.

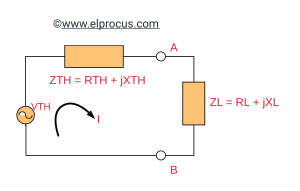
El circuito anterior es un circuito equivalente al de Thevenin. Cuando el circuito anterior se considera a través de la carga, el flujo de corriente se dará como

I = VTH / ZTH + ZL

Donde ZL = RL + jXL

ZTH = RTH + jXTH

En consecuencia,

I = VTH / (RL + jXL + RTH + jXTH )

= VTH / ((RL+ RTH) + j(XL + XTH ))

La potencia que fluye hacia la carga,

PL = I2 RL

PL = V2TH × RL / ((RL+ RTH)2 + (XL + XTH )2) ……(1)

Para la potencia más alta, la derivada de la ecuación anterior debe ser cero, después de la simplificación podemos obtener lo siguiente.

XL + XTH = 0

XL = – XTH

Sustituya el valor XL en la ecuación 1 anterior, luego podemos obtener lo siguiente.

PL = V2TH × RL / ((RL+ RTH) 2

Nuevamente, para la transferencia de potencia más alta, la derivación de la ecuación anterior debe ser igual a cero, después de resolver esto podemos obtener

RL + RTH = 2 RL

RL=DER

Por lo tanto, la potencia más alta se transmitirá desde el fuente a carga si RL (resistencia de carga) = RTH y XL = – XTH en un circuito de CA. Esto significa que la impedancia de carga (ZL) debe ser equivalente a la ZTH (complejo conjugado de la impedancia del circuito correspondiente)

ZL = ZTH

Esta potencia máxima transmitida (Pmax) = V2TH/ 4 RL o V2TH / 4 RTH

Teorema de transferencia de potencia máxima para circuitos de CC

El MPTT se utiliza en circuitos de CC que define la declaración de la transferencia de potencia más alta desde una red activa a una resistencia de carga externa. Define que en una corriente continua n/w activa, lineal, de dos lados, la fuente de alimentación suministrará la potencia más alta a la carga eléctrica una vez que la resistencia de la carga externa sea igual a la resistencia interna de la fuente de alimentación.

El desarrollo de MPTT se puede hacer por referencia a una fuente de voltaje o una corriente práctica. Si la fuente de poder es una fuente de voltaje independiente o práctica, su resistencia en serie interna debe ser igual a la resistencia de carga para transmitir la potencia más alta.

Una fuente de corriente independiente o una resistencia interna paralela práctica debe ser igual a la resistencia de carga. La resistencia en serie de la fuente interna en el circuito de CC cambia la potencia transmitida a la carga y, por lo tanto, se limita la corriente máxima transmitida desde la fuente de alimentación a la carga eléctrica.

Prueba MPTT

los prueba del teorema de transferencia de máxima potencia es, en algunas aplicaciones, el propósito de un circuito es entregar la máxima potencia a una carga. Algunos ejemplos:

• Amplificadores estéreo
• transmisores de radio
• Material de comunicación

Si todo el circuito se reemplaza por su circuito equivalente de Thevenin, excepto la carga, como se muestra a continuación, la potencia absorbida por la carga es:

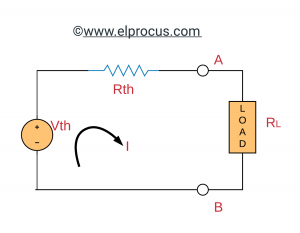
PAGS_L = yo² R_L = (V_mi/R_mi +R_L)² xR_L =V²_mi R_L/ (R_mi +R_L)²

Como VTH y RTH son fijos para un circuito dado, la potencia de carga es una función de la resistencia de carga RL.

Derivando PL con respecto a RL e igualando el resultado a cero, tenemos el siguiente teorema de máxima transferencia de potencia; La potencia máxima se produce cuando RL es igual a RTH.

Cuando se cumple la condición de transferencia de potencia máxima, es decir, RL=RTH, la potencia máxima transferida es:

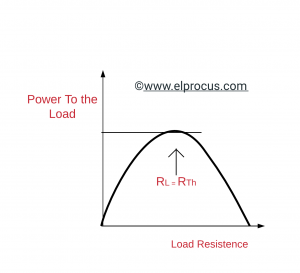
PAGS_L =V²_mi R_L / [R_th + R_L]² =V²_mi R_mi/ [R_th + R_L]² =V²_mi/ 4R_mi

Pasos para resolver la red usando el teorema de transferencia de potencia máxima

Los pasos a continuación se utilizan para resolver el problema mediante el teorema de transferencia de potencia máxima

Etapa 1: Retire la resistencia de carga del circuito.

2do paso: Encuentre la resistencia de Thevenin (RTH) de la red fuente observando los terminales de carga de circuito abierto.

Paso 3: De acuerdo con el teorema de transferencia de potencia máxima, RTH es la resistencia de carga de la red, es decir, RL = RTH que permite la transferencia de potencia máxima.

Paso 4: La transferencia de potencia máxima se calcula mediante la siguiente ecuación

(Pmáx) = V2TH / 4RTH

Teorema de Transferencia de Potencia Máxima Ejemplos de Problemas con Soluciones

Encuentre el valor de RL para el circuito debajo del cual la potencia también es la más alta, encuentre la potencia más alta a través de RL usando el teorema de transferencia de potencia máxima.

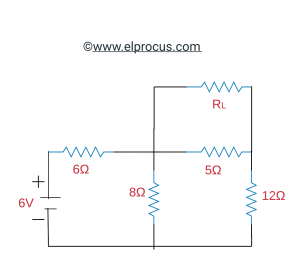
La solución:

De acuerdo con este teorema, cuando la potencia es máxima a través de la carga, la resistencia es similar a la resistencia igual entre los dos extremos de la RL después de retirarla.

Entonces, para encontrar la resistencia de carga (RL), necesitamos encontrar la resistencia equivalente:

Entonces,

Ahora, para encontrar la potencia más alta a través de la resistencia de carga RL, necesitamos encontrar el valor de voltaje entre los circuitos VOC.

Para el circuito anterior, aplique el análisis de malla. Se puede tener:

Aplicar KVL para loop-1:

6-6I1-8I1+8I2=0

-14I1+8I2=-6 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (1)

Aplicar KVL para loop-2:

-8I2-5I2-12I2+8I1=0

8I1-25I2=0 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (2)

Resolviendo las dos ecuaciones anteriores, obtenemos

I1 = 0.524A

I2 = 0.167A

Ahora desde el circuito Vo.c es

VA-5I2-VB = 0

Vo.c/ VAB= 5I2 = 5X0.167 = 0.835v

Por lo tanto, la potencia máxima a través de la resistencia de carga (RL) es;

Pmáx = V_CO² / 4R_L = (0,835 x 0,835)/ 4 x 3,77 = 0,046 vatios

Averigüe la potencia más alta que se puede pasar a la resistencia de carga RL en el siguiente circuito.

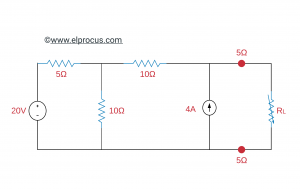
La solución

Aplique el teorema de Thevenin al circuito anterior,

Aquí, voltaje de Thevenin (Vth)= (200/3) y resistencia de Thevenin (Rth)=(40/3)Ω

Reemplace la fracción del circuito, que está a la izquierda de las terminales A y B del circuito dado por el circuito equivalente de Thevenin. El diagrama del circuito secundario se muestra a continuación.

Podemos encontrar la potencia máxima que se entregará a la resistencia de carga, RL, utilizando la siguiente fórmula.

PL, Máx = V2TH / 4RTH

Sustituya VTh = (200/3)V y RTh = (40/3)Ω en la fórmula anterior.

PL, Máx = (200/3)²/ 4(40/3) = 250/3 vatios

Por lo tanto, la potencia máxima que se entregará a la resistencia de carga RL del circuito dado es de 250/3 W.

Ventajas y desventajas

Las ventajas y desventajas del teorema de máxima transferencia de potencia son las siguientes.

• La principal ventaja del teorema de máxima transferencia de potencia es que puede analizar el rendimiento en cualquier momento.
• La principal desventaja del teorema de transferencia de potencia máxima es que no se usa en redes unilaterales y no lineales.
• La limitación del teorema de máxima transferencia de potencia no es aplicable en los sistemas eléctricos, debido a su eficiencia del 50%. Por lo tanto, la principal preocupación es la eficiencia.
• Este teorema se puede aplicar a las líneas de comunicación en lugar de las líneas eléctricas porque si lo aplicamos a las líneas eléctricas, surgirán los siguientes problemas prácticos.
• En las líneas eléctricas, la constancia del voltaje del extremo receptor es una condición importante, por lo que este teorema ignora esta característica.
• Debido a la menor eficiencia, esto no se puede aceptar en las líneas eléctricas.

Aplicaciones del teorema de transferencia de máxima potencia

el teorema de transferencia de potencia máxima puede aplicarse de varias maneras para determinar el valor de la resistencia de carga que recibe la potencia máxima de la fuente y la potencia máxima en el estado de mayor transferencia de potencia. Aquí hay algunas aplicaciones del teorema de transferencia de potencia máxima:

• Este teorema siempre se busca en un sistema de comunicación. Por ejemplo, en un sistema de direcciones comunitarias, el El circuito está ajustado para la transferencia de potencia más alta al hacer que el altavoz (resistencia de carga) sea equivalente al amplificador (resistencia de fuente). Cuando la carga y la fuente coinciden, la resistencia es igual.
• En los motores de automóviles, la potencia transmitida al motor de arranque del automóvil dependerá de la resistencia efectiva del motor y de la resistencia interna de la batería. Cuando las dos resistencias sean iguales, se transmitirá la potencia más alta al motor para activar el motor.
• El teorema de transferencia de potencia máxima se puede aplicar en la red compleja de la siguiente manera
• Se utiliza en redes de CA y CC.
• Para obtener la máxima transferencia de potencia en el sistema de sonido, el circuito se puede modificar haciendo que la RL (resistencia de carga) como un altavoz sea equivalente a la resistencia de la fuente como un amplificador. Una vez que la fuente y la carga incluyen la resistencia equivalente, se igualan.
• Este teorema se usa donde todas las fuentes de voltaje autónomas están apagadas y simplemente se considera la misma impedancia, entonces se puede transmitir una cantidad máxima de energía.
• En comunicaciones por radio, se utiliza cuando el amplificador de potencia irradia la mayor cantidad de señal a la antena si la impedancia de carga en el circuito es equivalente a la impedancia de la fuente.
• En los sistemas de audio se utiliza donde es necesario entregarlo al hablante. El amplificador cambia la cantidad de voz más alta una vez que la impedancia de carga es igual a la impedancia de la fuente.
• En una red resistiva, una carga resistiva extraerá la potencia máxima una vez que la resistencia de la carga sea equivalente a la resistencia que se ve a través de la carga cuando mira hacia la red.
  De hecho, la resistencia es accesible a los terminales de salida de la red. De hecho, esta resistencia es la resistencia equivalente de Thevenin que se describe en el teorema de Thevenin si consideramos la red completa como una fuente de voltaje. De manera similar, si consideramos la red como una fuente de corriente, esta resistencia se denominará resistencia equivalente de Norton, que puede describirse en el teorema de Norton.
• Se utiliza en todo tipo de circuitos donde los circuitos están diseñados en base al principio de eficiencia que se reducirá en un 50%. Sin embargo, los consumidores usan este MPTT en áreas donde la potencia es limitada, como receptores móviles y altavoces.
• Esta menor eficiencia puede ser soportada en nombre de la mayor potencia a entregar a la carga utilizada en la red. En los sistemas eléctricos, las caídas de tensión y las pérdidas de potencia en los generadores, así como en los sistemas de transmisión, se consideran menores.
• Aquí la impedancia de carga es muchas veces mayor que la impedancia interna de la fuente
• En consecuencia, los circuitos de potencia operan por debajo de las condiciones óptimas de adaptación. Por ejemplo, en la transmisión de energía, donde importa la mayor eficiencia, diseñamos sistemas basados ​​en el voltaje más alto. Pero no es posible resistir la disipación de calor debido a la pérdida del 50%, porque la potencia de salida es de cien MW.

Este es el teorema de la máxima potencia. De la información anterior, finalmente, podemos concluir que este teorema se usa a menudo para garantizar que la potencia más alta se pueda transmitir desde una fuente de alimentación a una carga. Aquí hay una pregunta para usted, ¿cuál es el beneficio del Teorema de Transferencia de Potencia Máxima?