Como sabe, un filtro de paso alto está diseñado para pasar todas las frecuencias por encima de su frecuencia de corte. Los filtros de paso alto se crean invirtiendo las posiciones de los componentes resistivos y reactivos en el Filtros de paso bajo RC y RL.
En este artículo, discutiremos cómo funcionan los filtros de paso alto RC y RL. Como verá, la mayoría de las relaciones de los filtros de paso alto son casi las mismas que las de los filtros de paso bajo, ya que la principal diferencia entre un filtro de paso alto y su contraparte de paso bajo es la ubicación de los componentes.
Filtros de paso alto RC
Un circuito RC actúa como un filtro de paso alto cuando se construye como se muestra en la figura. Imagen 1a. A modo de comparación, se muestra un filtro de paso bajo RC i Figura 1b. Como puede ver, las posiciones de los capacitores y las resistencias están invertidas entre los dos circuitos. En el circuito de paso alto, el capacitor está en la ruta de la señal y la resistencia es el componente de derivación.
Figura 1: Filtros paso alto o paso bajo
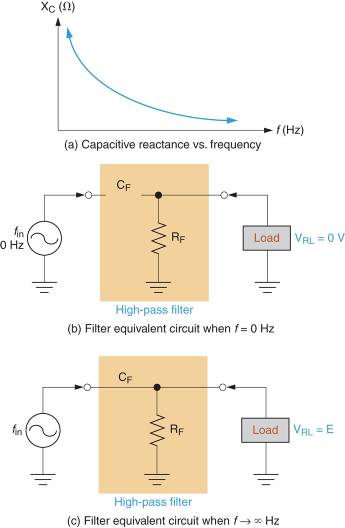
Acción filtrante del circuito de entrada Imagen 1a como resultado de la respuesta del condensador a un aumento en la frecuencia. Esta respuesta se muestra en Figura 2. La curva de reactancia (que usamos para describir el funcionamiento del filtro de paso bajo) muestra que la reactancia capacitiva varía inversamente con la frecuencia de funcionamiento. Con eso en mente, mire el circuito equivalente que se muestra en Figura 2b. Como puede ver, la reactancia casi infinita del condensador cuando la frecuencia de entrada es de 0 Hz aparece como una interrupción en la ruta de la señal. Por lo tanto, la fuente está aislada de la carga y VRL = 0V.
Figura 2: Cómo funciona el filtro de paso alto RC
Suponiendo que la frecuencia de entrada está cerca del extremo superior de la curva de reacción, Xcontra se puede suponer que es alrededor de 0 Ω. Con eso en mente, mire el circuito equivalente como se muestra en Figura 2c. En este caso, el capacitor de baja reactancia está representado por una conexión directa entre la fuente y la carga. En consecuencia, el voltaje de la carga es aproximadamente igual al voltaje de la fuente.
Entre los extremos mostrados en la Figura 2, existe un rango de frecuencias con VRL V disminuyeRL≅E a VRL = 0V.
Frecuencia de corte inferior (fcontra)
La frecuencia de corte para a antes de Cristo determinar un filtro de paso alto usando la misma relación que establecimos para el filtro de paso bajo. Según fórmula,
[{{f}_{C}}=frac{1}{2pi RC}]
Podemos usar esta relación porque solo han cambiado las posiciones de los componentes en el filtro. En otras palabras, la relación entre fcontraR y C no cambian simplemente porque la ubicación de los componentes ha cambiado. Ejemplo 1 ilustra el proceso utilizado para calcular la frecuencia de corte de un filtro de paso alto RC.
Ejemplo 1
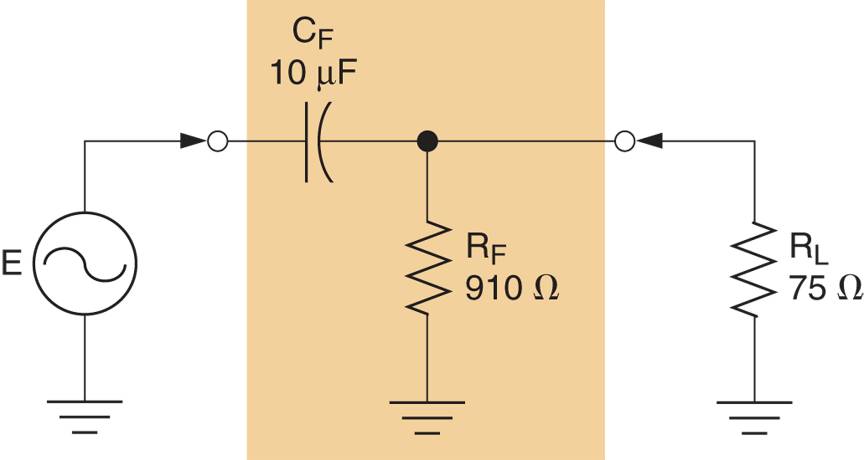
Calcule la frecuencia de corte del filtro de paso alto RC en la Figura 2a.
Figura 2a
La solución
Primero, la resistencia del circuito (vista por el capacitor) se encuentra de la siguiente manera:
[{{R}_{EQ}}={{R}_{F}}||{{R}_{L}}=frac{75times 910}{75+910}=69.3Omega ]
Ahora la frecuencia de corte del circuito se puede encontrar de la siguiente manera:
[{{f}_{C}}=frac{1}{2pi RC}=frac{90.1Omega }{2pi times 69.3Omega times 10mu F}=230Hz]
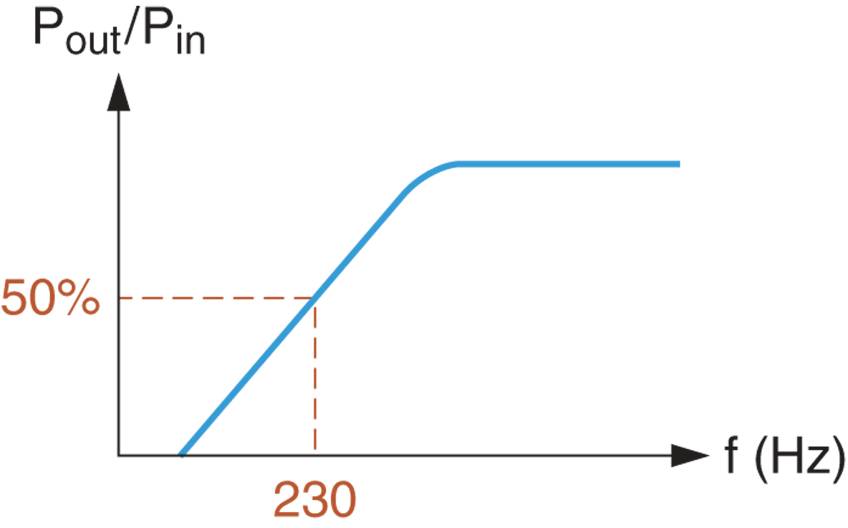
Este resultado muestra que la ganancia de potencia del circuito disminuye al 50% de su valor máximo cuando la frecuencia de operación disminuye a 230 Hz. La curva de respuesta de frecuencia del circuito se muestra en Figura 2b.
Figura 2b: Curva de respuesta de frecuencia
Filtros de paso alto RL
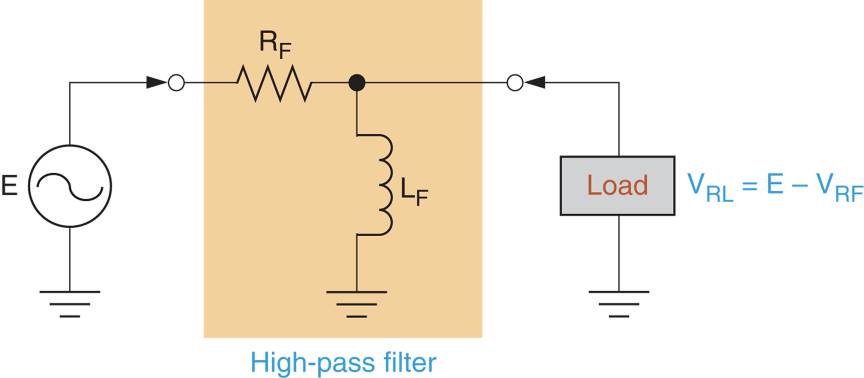
Un circuito RL actúa como un filtro de paso alto cuando se construye como se muestra en la figura. imagen 3. En el circuito que se muestra, la resistencia es el componente en serie y el inductor es el componente en derivación.
Figura 3: filtro de paso alto RL
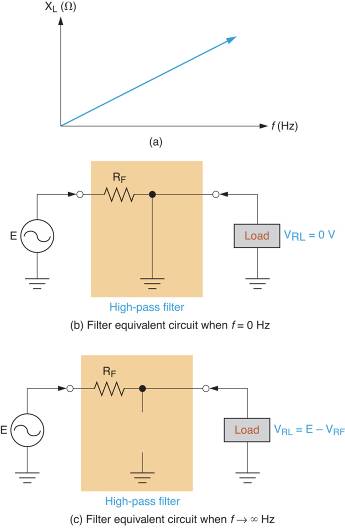
La acción de filtrado del circuito de la Figura 3 es el resultado de la respuesta de los inductores a una disminución en la frecuencia de operación. Esta respuesta se muestra en Figura 4. Como se muestra en la curva de reacción, XL tiende a infinito a medida que aumenta la frecuencia.
Si la frecuencia de entrada se reduce a 0 Hz, la reactancia inductiva se reduce a 0 Ω. En este caso, el circuito equivalente i Figura 4b función. Ignorando la pequeña cantidad de resistencia de devanado en la bobina, el inductor en derivación se muestra como en un cortocircuito camino a la tierra. En este caso, V.RL = 0V.
Figura 4: Funcionamiento del filtro de paso alto RL
Si la frecuencia de entrada del circuito aumenta, la reactancia del inductor aumentará hasta que el componente actúe efectivamente como un abierto. Si suponemos que XL ≡ ∞Ω, el circuito equivalente i Figura 4c función. Como puede ver, el inductor se representa como una interrupción en la ruta del componente de derivación. En este caso, V.RL = VERF. Entre los extremos mostrados en la Figura 4, existe un rango de frecuencias con VRL disminuir de E a VRF a 0V.
Frecuencia de corte inferior (fcontra)
La inductancia y la combinación paralela de R determinan la frecuencia de corte más baja para un filtro de paso alto RLF y RL. Según fórmula:
[{{f}_{C}}=frac{{{R}_{EQ}}}{2pi L}]
¿Dónde estará R?igualada =RF || RL.
Ejemplo 2 ilustra el proceso utilizado para calcular la frecuencia de corte de un filtro de paso alto RL.
Ejemplo 2
Calcule la frecuencia de corte para el filtro de paso alto RL en la Figura 4a.
Imagen 4a
La solución
Primero, la resistencia del circuito (vista por el capacitor) se encuentra de la siguiente manera:
[{{R}_{EQ}}={{R}_{F}}||{{R}_{L}}=frac{100times 910}{100+910}=90.1Omega ]
Ahora la frecuencia de corte del circuito se puede encontrar de la siguiente manera:
[{{f}_{C}}=frac{{{R}_{EQ}}}{2pi C}=frac{90.1Omega }{2pi times 47mH}=305Hz]
Este resultado muestra que la ganancia de potencia del circuito se reduce al 50% de su valor máximo cuando la frecuencia de operación se reduce a 305 Hz. La curva de respuesta de frecuencia del circuito se muestra en Figura 4b.
Figura 4b: Curva de respuesta de frecuencia
Como puede ver, el análisis de un circuito RL de paso alto es idéntico al análisis de un filtro de paso bajo RL.



¡Más Contenido!