Explicación de la Media Suma y la Suma Completa con Tabla Verdadera

En los circuitos combinacionales, se utilizan diferentes puertas lógicas para diseñar codificadores, multiplexores, decodificadores y desmultiplexores. Estos circuitos tienen algunas características como que la salida de este circuito depende principalmente de los niveles que hay en los terminales de entrada en cada momento. Este circuito no incluye ninguna memoria. El estado anterior de la entrada no influye en el estado actual de este circuito. Las entradas y salidas de un circuito combinacional son "n" números de entradas y "m" números de salidas. Algunos de los circuitos combinacionales son la media suma y la suma completa, el sustractor, el codificador, el decodificador, el multiplexor y el demultiplexor. Este artículo trata de una visión general de la media suma y la suma completa y su funcionamiento con tablas de verdad.

¿Qué es un sumador?

Un sumador es un circuito lógico digital en electrónica que se utiliza ampliamente para la suma de números. En muchos ordenadores y otros tipos de procesadores, los sumadores se utilizan incluso para calcular direcciones y actividades relacionadas y calcular índices de tablas en la ALU e incluso se utilizan en otras partes de los procesadores. Se pueden construir para muchas representaciones numéricas como el exceso-3 o el decimal codificado en binario. Los sumadores se clasifican básicamente en dos tipos: Sumador medio y Sumador completo.

¿Qué es el circuito de medio sumador y sumador completo?

El circuito semiconsumidor tiene dos entradas: A y B, que suman dos dígitos de entrada y generan un acarreo y una suma. El circuito sumador completo tiene tres entradas: A y C, que suman tres números de entrada y generan un acarreo y una suma. Este artículo ofrece información detallada sobre la finalidad de un semiconsumidor y sumador completo en formas tabulares e incluso en diagramas de circuito también. Ya se ha mencionado que el propósito principal y crucial de los sumadores es la adición. A continuación se detallan la teoría del medio sumador y del sumador completo.

Media Suma

En el caso de la media suma, se suman dos dígitos binarios en los que los bits de entrada se denominan augend y addend, y el resultado serán dos salidas: una es la suma y la otra es el carry. Para realizar la operación de suma, se aplica el XOR a ambas entradas, y la puerta AND se aplica a ambas entradas para producir el acarreo.

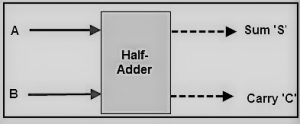
Mientras que en el circuito sumador completo, se suman 3 números de un bit, donde dos de los tres bits pueden denominarse operandos y el otro se denomina bit transportado. La salida producida es de 2 bits y se pueden denominar acarreo y suma de salida.

Utilizando un semi-sumador, puedes diseñar sumas sencillas con la ayuda de puertas lógicas.

Veamos un ejemplo de adición de dos bits simples.

La suma de 2 bits tabla de verdad del semiconsumidor es la siguiente:

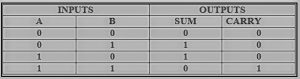
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10

Estas son las menores combinaciones posibles de un solo bit. Pero como el resultado de 1+1 es 10, el resultado de la suma debe reescribirse como una salida de 2 bits. Así, las ecuaciones pueden escribirse como

0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10

La salida "1" de "10" es el arrastre. la "SUMA" es la salida normal y la "CARRERA" es el arrastre.

Ahora queda claro que se puede implementar fácilmente un sumador de 1 bit con la ayuda de la puerta XOR para la salida "SUM" y una puerta AND para el "carry".

Por ejemplo, cuando necesitamos sumar dos bytes de 8 bits, se puede implementar utilizando un circuito lógico de escalera completa. La media escalera es útil cuando quieres sumar cantidades de un dígito binario.

Una forma de desarrollar sumadores de dos dígitos binarios sería hacer una tabla de verdad y reducirla. Cuando quieras hacer un sumador de tres dígitos binarios, la operación de adición del medio sumador se realiza dos veces. De forma similar, cuando decides hacer un sumador de cuatro dígitos, la operación se realiza una vez más. Con esta teoría, quedó claro que la implementación es sencilla, pero el desarrollo es un proceso que lleva tiempo.

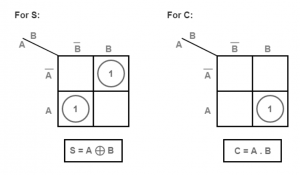
La expresión más sencilla utiliza la función OR exclusiva:

Suma= A XOR B

Carga = A Y B

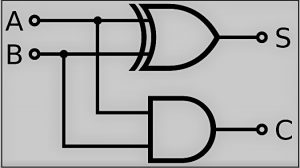
Y una expresión equivalente en términos de los básicos Y, O y NO es:

SUM=A.B+A.B'

Código VHDL para el medio sumador

La entidad ha es

Puerto (a: en STD_LOGIC;
b : en STD_LOGIC;
sha : out STD_LOGIC;
cha : out STD_LOGIC);
fin ha;

Arquitectura El comportamiento del circuito anterior es

empezar
sha <= a xor b ;
cha <= a y b ;
fin Comportamiento

Número de CI del semiconservador

La implementación del medio sumador puede realizarse mediante circuitos integrados lógicos digitales CMOS de alta velocidad, como la serie 74HCxx, que incluye el SN74HC08 (7408) y el SN74HC86 (7486).

Limitaciones del Semisumador

La razón principal para llamar a estos sumadores binarios como medios sumadores es que no hay margen para incluir el bit de arrastre utilizando un bit anterior. Por tanto, ésta es una de las principales limitaciones de los AH que se utilizan como sumadores binarios, especialmente en situaciones de tiempo real que implican la suma de varios bits. Así que esta limitación puede superarse utilizando los sumadores completos.

Sumador completo

Este sumador es difícil de implementar si se compara con la media suma.

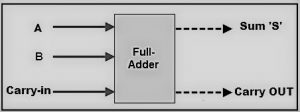
La diferencia entre una media escalera y una escalera completa es que la escalera completa tiene tres entradas y dos salidas, mientras que la media escalera sólo tiene dos entradas y dos salidas. Las dos primeras entradas son A y B y la tercera es una entrada de acarreo como C-IN. Cuando se diseña una lógica de escalera completa, se encadenan ocho de ellas para crear un sumador a lo largo de todo un byte y se lleva en cascada el bit de acarreo de un sumador al siguiente.

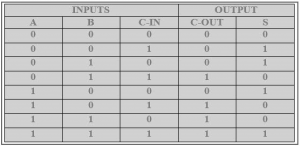
El acarreo de salida se designa como C-OUT y la salida normal se representa como S que es "SUM".

Con lo anterior tabla de verdad del sumador completola implementación de un circuito sumador completo se puede entender fácilmente. La suma "S" se produce en dos pasos:

1. Xorando las entradas "A" y "B" proporcionadas
2. El resultado de A XOR B se XORiza con el C-IN

Esto genera la SUMA y la C-SALIDA es verdadera sólo cuando dos de las tres entradas son ALTAS, entonces la C-SALIDA será ALTA. Por tanto, podemos implementar un circuito sumador completo con la ayuda de dos circuitos semi sumadores. Inicialmente, el medio sumador se utilizará para sumar A y B para producir una suma parcial y se puede utilizar una lógica de segundo medio sumador para añadir C-IN a la suma producida por el primer medio sumador para obtener la salida final S.

Si alguna de las lógicas de los semi sumadores produce un acarreo, habrá un acarreo de salida. Por lo tanto, C-OUT será una función OR de las salidas de acarreo de la media suma. Observa la implementación del circuito sumador completo que se muestra a continuación.

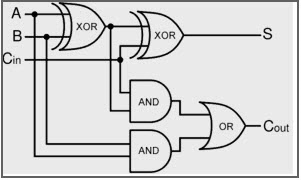
La implementación de diagramas lógicos más grandes es posible con la lógica del sumador completo anterior, se suele utilizar un símbolo más sencillo para representar la operación. A continuación se muestra una representación esquemática más sencilla de un sumador completo de un bit.

Con este tipo de símbolo, podemos sumar dos bits, tomando un acarreo del siguiente orden de magnitud inferior, y enviando un acarreo al siguiente orden de magnitud superior. En un ordenador, para una operación de varios bits, cada bit debe estar representado por un sumador completo y debe sumarse simultáneamente. Así, para sumar dos números de 8 bits, necesitarás 8 sumadores completos que pueden formarse conectando en cascada dos de los bloques de 4 bits.

Medio sumador y sumador completo con K-Map

También se pueden obtener las salidas de suma y acarreo de un medio sumador con el método del mapa de Karnaugh (mapa K). El expresión booleana del medio sumador y del sumador completo puede obtenerse mediante el mapa K. Por lo tanto, a continuación se analiza el mapa K de estos sumadores.

El mapa K de los semi sumadores es

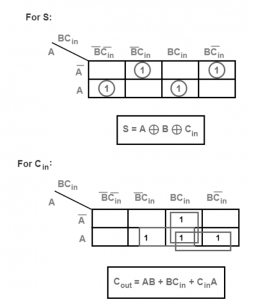
El mapa K del sumador completo es

Expresión lógica de la suma y el acarreo

La expresión lógica de la suma (S) puede determinarse a partir de las entradas mencionadas en la tabla.

= A'B'Cin + A' B CCin' + A B'Cin'+ AB Cin
= Cin (A'B'+ AB) + Cin' (A'B +A B')
= Cin EX-OR (A EX-OR B)
= (1,2,4,7)

La expresión lógica del acarreo (Cout) puede determinarse a partir de las entradas mencionadas en la tabla.

= A'B Cin + AB'Cin + AB Cin' + ABCin
= AB + BCin + ACin
= (3, 5, 6, 7)

Con las tablas de verdad mencionadas, se pueden obtener los resultados y el procedimiento es :

Un circuito combinacional combina las diferentes puertas del circuito, que pueden ser un codificador, un decodificador, un multiplexor y un demultiplexor. Las características de los circuitos combinacionales son las siguientes

• La salida en cualquier instante de tiempo se basa únicamente en los niveles presentes en los terminales de entrada.
• No utiliza ninguna memoria. El estado anterior de la entrada no tiene ningún efecto sobre el estado actual del circuito.
• Puede tener cualquier número de entradas y m número de salidas.

Codificación VHDL

Codificación VHDL del sumador completo incluye lo siguiente.

la entidad full_add es

Puerto ( a : en STD_LOGIC;
b : en STD_LOGIC;
cin : en STD_LOGIC;
sum : out STD_LOGIC;
cout : out STD_LOGIC);
fin full_add;

Arquitectura El comportamiento de full_add es

el componente ha es
Puerto ( a : en STD_LOGIC;
b : en STD_LOGIC;
sha : out STD_LOGIC;
cha : out STD_LOGIC);
fin del componente;
señal s_s,c1,c2: STD_LOGIC ;
comenzar
HA1:ha port map(a,b,s_s,c1);
HA2:ha port map(s_s,cin,sum,c2);
cout<=c1 o c2 ;
fin Comportamiento;

El diferencia entre medio sumador y sumador completo es que el medio sumador produce resultados y el sumador completo utiliza el medio sumador para producir algún otro resultado. Del mismo modo, mientras que el sumador completo está formado por dos medios sumadores, el sumador completo es el bloque real que utilizamos para crear los circuitos aritméticos.

Sumadores de seguimiento de la carga

En el concepto de circuitos sumadores de acarreo ondulado, los bits necesarios para la suma están disponibles inmediatamente. En cambio, cada sección del sumador tiene que esperar la llegada del acarreo del bloque sumador anterior. Por ello, se necesita más tiempo para producir la SUMA y el CARRITO, ya que cada sección del circuito espera la llegada de la entrada.

Por ejemplo, para entregar la salida del bloque n, tiene que recibir la entrada del bloque (n-1). Y este retardo se denomina correspondientemente retardo de propagación.

Para superar el retardo en el sumador de ripple carries, se introdujo un sumador de carry-lookahead. Aquí, utilizando un hardware complicado, se puede minimizar el retardo de propagación. El siguiente diagrama muestra un sumador de arrastre que utiliza sumadores completos.

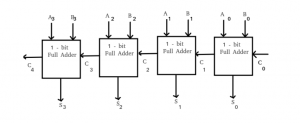
La tabla de verdad y las ecuaciones de salida correspondientes son

A	B	C	C+1	Condición
0	0	0	0	No hay transporte Generar
0	0	1	0
0	1	0	0
0	1	1	1	No hay transporte Propagar
1	0	0	0
1	0	1	1
1	1	0	1	Llevar Generar
1	1	1	1

La ecuación de propagación del acarreo es Pi = Ai XOR Bi y la generación del acarreo es Gi = Ai*Bi. Con estas ecuaciones, las ecuaciones de suma y acarreo pueden representarse como

SUMA = Pi XOR Ci

Ci+1 = Gi + Pi*Ci

Gi entrega el acarreo sólo cuando las dos entradas Ai y Bi son 1, sin tener en cuenta el acarreo de la entrada. Pi está relacionado con la propagación del acarreo de Ci a Ci+1.

Diferencia entre el medio sumador y el sumador completo

El diferencia entre la tabla del semiconsumidor y la del sumador completo se muestra a continuación.

Media Suma	Suma completa
El medio sumador (HA) es un circuito lógico combinacional que se utiliza para sumar dos dígitos de un bit.	El sumador completo (FA) es un circuito combinacional que se utiliza para sumar tres dígitos de un bit.
En el HA, una vez que se genera el acarreo de la suma anterior no se puede añadir al siguiente paso.	En FA, una vez que se genera el acarreo de la adición anterior, se puede añadir al paso siguiente.
La media suma incluye dos puertas lógicas como la puerta AND y la puerta EX-OR.	El sumador completo incluye dos puertas EX-OR, dos puertas OR y dos puertas AND.
Los bits de entrada en la media suma son dos como A, B.	Los bits de entrada en el sumador completo son tres como A, B y C-in
La ecuación de la suma y el acarreo en el sumador parcial es S = a⊕b ; C = a*b	La expresión lógica del sumador completo es S = a ⊕ b⊕Cin; Cout = (a*b) + (Cin*(a⊕b)).
La HA se utiliza en ordenadores, calculadoras, aparatos de medición digital, etc.	FA se utiliza en los procesadores digitales, en la suma de varios bits, etc.

El diferencias clave entre el semi sumador y el sumador completo se discuten a continuación.

• El medio sumador genera la suma y el acarreo sumando dos entradas binarias, mientras que el sumador completo se utiliza para generar la suma y el acarreo sumando tres entradas binarias. La arquitectura de hardware del medio sumador y del sumador completo no es la misma.
• La principal característica que diferencia al HA y al FA es que en el HA no se considera el último acarreo de la suma como su entrada. Pero, un FA localiza una columna de entrada concreta como Cin para considerar el bit de acarreo de la última suma.
• Los dos sumadores presentan una diferencia basada en los componentes utilizados en el circuito para su construcción. Los medios sumadores (HA) están diseñados con la combinación de dos puertas lógicas como AND y EX-OR, mientras que el FA está diseñado con la combinación de tres puertas AND, dos XOR y una OR.
• Básicamente, los HA funcionan con dos entradas de 1 bit, mientras que los FA funcionan con tres entradas de 1 bit. El medio sumador se utiliza en diferentes dispositivos electrónicos para evaluar la suma, mientras que el sumador completo se utiliza en los procesadores digitales para la suma de un bit largo.
• Las similitudes de estos dos sumadores son que tanto el HA como el FA son circuitos digitales combinacionales, por lo que no utilizan ningún elemento de memoria como los circuitos secuenciales. Estos circuitos son esenciales para que la operación aritmética proporcione la suma del número binario.

Implementación de un sumador completo con medios sumadores

La implementación de un FA puede realizarse mediante dos medios sumadores que se conectan lógicamente. A continuación se muestra el diagrama de bloques que indica la conexión de un FA mediante dos medios sumadores.
Las ecuaciones de suma y acarreo de los cálculos anteriores son

S = A' B' Cin + A' BC' in + ABCin

Cout = AB + ACin + BCin

La ecuación de la suma puede escribirse como

Cin (A'B '+ AB) + C 'en (A'B + A B')

Por tanto, Suma = Cin EX-OR (A EX-OR B)

Cin (A EX-OR B) + C'in (A EX-OR B)

= Cin EX-OR (A EX-OR B)

Cout se puede escribir de la siguiente manera

COUT = AB + ACin + BCin.

COUT = AB + ACin+ BCin (A + ̅A)

= ABCin + AB + ACin + A' B Cin

= AB (1 + Cin) + ACin + A' B Cin

= A B + ACin + A' B Cin

= AB + ACin (B + B' ) + A' B Cin

= ABCin + AB + A'B Cin+ A' B Cin

= AB (Cin + 1) + A B Cin + A' B Cin

= AB + AB' Cin + A' B Cin

= AB + Cin ( AB' + A'B )

Por tanto, COUT = AB + Cin (A EX-OR B)

En función de las dos ecuaciones de suma y acarreo anteriores, el circuito FA puede implementarse con la ayuda de dos HA y una puerta OR. El diagrama del circuito de un sumador completo con dos medios sumadores se ilustra arriba.

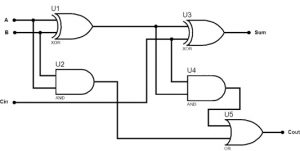
Diseño de un sumador completo con puertas NAND

Una puerta NAND es un tipo de puerta universal, utilizada para ejecutar cualquier tipo de diseño lógico. El circuito FA con el diagrama de las puertas NAND se muestra a continuación.

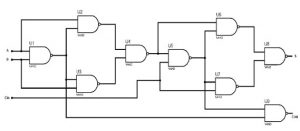
El FA es un sumador sencillo de un bit y si deseamos ejecutar la suma de n bits, entonces hay que emplear n nº de FAs de un bit en el formato de conexión en cascada.

Ventajas

El ventajas del semiconsumidor y del sumador completo incluyen las siguientes.

• El objetivo principal de un semi-sumador es sumar dos números de un solo bit
• Los sumadores completos tienen la capacidad de añadir un bit de arrastre que es el resultado de la suma anterior
• Con el sumador completo se pueden implementar circuitos cruciales como el sumador, el multiplexor y muchos otros
• Los circuitos sumadores completos consumen una potencia mínima
• Las ventajas de un sumador completo sobre un medio sumador son que el sumador completo se utiliza para superar el inconveniente de un medio sumador porque el medio sumador se utiliza principalmente para sumar dos números de 1 bit. Los sumadores medios no añaden el bit de arrastre, por lo que para superar esto se emplea el sumador completo. En el sumador completo se pueden sumar tres bits y se generan dos salidas.
• El diseño de los sumadores es sencillo y se trata de un bloque de construcción básico para que la adición de un bit pueda entenderse fácilmente.
• Este sumador se puede convertir en medio restador añadiendo un inversor.
• Utilizando un sumador completo, se puede obtener una salida elevada.
• Alta velocidad
• Muy resistente al escalado de la tensión de alimentación

Desventajas

El desventajas del semi sumador y del sumador completo incluyen las siguientes.

• Además, el semiconsumidor no puede utilizar el transporte previo, por lo que no es aplicable para la adición en cascada de varios bits.
• Para superar este inconveniente, es necesario que FA sume tres 1 bits.
• Una vez que el FA se utiliza en forma de cadena como un RA (sumador de ondas), la capacidad de accionamiento de la salida puede disminuir.

Aplicaciones

Las aplicaciones de la media sumadora y la sumadora completa son las siguientes

• La adición de bits binarios puede realizarse mediante el medio sumador utilizando la ALU dentro del ordenador, ya que utiliza el sumador.
• La combinación de medios sumadores puede utilizarse para diseñar un circuito sumador completo.
• Los medios sumadores se utilizan en las calculadoras y para medir las direcciones, así como las tablas
• Estos circuitos se utilizan para manejar diferentes aplicaciones dentro de los circuitos digitales. En el futuro, desempeñan un papel fundamental en la electrónica digital.
• Un circuito FA se utiliza como elemento en muchos circuitos grandes, como el sumador de acarreo de ondas. Este sumador suma el número de bits simultáneamente.
• Los FA se utilizan en la Unidad Lógica Aritmética (ALU)
• Los AF se utilizan en aplicaciones relacionadas con los gráficos como la GPU (Unidad de Procesamiento Gráfico)
• Se utilizan en el circuito de multiplicación para ejecutar la Multiplicación Carryout.
• En un ordenador, para generar la dirección de memoria y construir el contrapunto del programa hacia la instrucción posterior, se utiliza la Unidad Lógica Aritmética mediante el uso de Sumadores Completos.

Así, cada vez que se realiza la suma de dos números binarios, los dígitos se suman primero los menos bits. Este proceso puede realizarse a través de un medio sumador, ya que es el más sencillo n/w que permite sumar dos números de 1 bit. Las entradas de este sumador son los dígitos binarios, mientras que las salidas son la suma (S) y el acarreo (C).

Cuando se incluye el número de dígitos, la red HA se utiliza simplemente para conectar los dígitos menores, ya que la HA no puede añadir el número de acarreo de la clase anterior. Un sumador completo puede definirse como la base de todos los dispositivos aritméticos digitales. Se utiliza para sumar tres números de 1 dígito. Este sumador incluye tres entradas como A, B y Cin, mientras que las salidas son Suma y Cout.

Conceptos relacionados

El conceptos relacionados con el medio sumador y el sumador completo no se ciñen a un único propósito. Tienen un amplio uso en muchas aplicaciones y se mencionan algunas de las relacionadas:

• Número de CI del sumador medio y del sumador completo
• Desarrollo del sumador de 8 bits
• ¿Cuáles son las precauciones del medio sumador?
• Applet JAVA de una sumadora de acarreo de ondas

Por tanto, se trata de la teoría del medio sumador y del sumador completo junto con las tablas de verdad y los diagramas lógicos, también se muestra el diseño del sumador completo utilizando el circuito del medio sumador. Muchos de los medio sumador y sumador completo pdf hay documentos que proporcionan información avanzada de estos conceptos. Además, es importante saber cómo se implementa un sumador completo de 4 bits?